High-accuracy sampling for diffusion models and log-concave distributions

We present algorithms for diffusion model sampling which obtain $δ$-error in $\mathrm{polylog}(1/δ)$ steps, given access to $\widetilde O(δ)$-accurate score estimates in $L^2$. This is an exponential improvement over all previous results. Specifically, under minimal data assumptions, the complexity is $\widetilde O(d\,\mathrm{polylog}(1/δ))$ where $d$ is the dimension of the data; under a non-uniform $L$-Lipschitz condition, the complexity is $\widetilde O(\sqrt{dL}\,\mathrm{polylog}(1/δ))$; and if the data distribution has intrinsic dimension $d_\star$, then the complexity reduces to $\widetilde O(d_\star\,\mathrm{polylog}(1/δ))$. Our approach also yields the first $\mathrm{polylog}(1/δ)$ complexity sampler for general log-concave distributions using only gradient evaluations.

Ambient Dataloops: Generative Models for Dataset Refinement

We propose Ambient Dataloops, an iterative framework for refining datasets that makes it easier for diffusion models to learn the underlying data distribution. Modern datasets contain samples of highly varying quality, and training directly on such heterogeneous data often yields suboptimal models. We propose a dataset-model co-evolution process; at each iteration of our method, the dataset becomes progressively higher quality, and the model improves accordingly. To avoid destructive self-consuming loops, at each generation, we treat the synthetically improved samples as noisy, but at a slightly lower noisy level than the previous iteration, and we use Ambient Diffusion techniques for learning under corruption. Empirically, Ambient Dataloops achieve state-of-the-art performance in unconditional and text-conditional image generation and de novo protein design. We further provide a theoretical justification for the proposed framework that captures the benefits of the data looping procedure.

Learning Gaussian DAG Models without Condition Number Bounds

We study the problem of learning the topology of a directed Gaussian Graphical Model under the equal-variance assumption, where the graph has $n$ nodes and maximum in-degree $d$. Prior work has established that $O(d \log n)$ samples are sufficient for this task. However, an important factor that is often overlooked in these analyses is the dependence on the condition number of the covariance matrix of the model. Indeed, all algorithms from prior work require a number of samples that grows polynomially with this condition number. In many cases this is unsatisfactory, since the condition number could grow polynomially with $n$, rendering these prior approaches impractical in high-dimensional settings. In this work, we provide an algorithm that recovers the underlying graph and prove that the number of samples required is independent of the condition number. Furthermore, we establish lower bounds that nearly match the upper bound up to a $d$-factor, thus providing an almost tight characterization of the true sample complexity of the problem. Moreover, under a further assumption that all the variances of the variables are bounded, we design a polynomial-time algorithm that recovers the underlying graph, at the cost of an additional polynomial dependence of the sample complexity on $d$. We complement our theoretical findings with simulations on synthetic datasets that confirm our predictions.

DiffEM: Learning from Corrupted Data with Diffusion Models via Expectation Maximization

Diffusion models have emerged as powerful generative priors for high-dimensional inverse problems, yet learning them when only corrupted or noisy observations are available remains challenging. In this work, we propose a new method for training diffusion models with Expectation-Maximization (EM) from corrupted data. Our proposed method, DiffEM, utilizes conditional diffusion models to reconstruct clean data from observations in the E-step, and then uses the reconstructed data to refine the conditional diffusion model in the M-step. Theoretically, we provide monotonic convergence guarantees for the DiffEM iteration, assuming appropriate statistical conditions. We demonstrate the effectiveness of our approach through experiments on various image reconstruction tasks.

Ambient Diffusion Omni: Training Good Models with Bad Data

We show how to use low-quality, synthetic, and out-of-distribution images to improve the quality of a diffusion model. Typically, diffusion models are trained on curated datasets that emerge from highly filtered data pools from the Web and other sources. We show that there is immense value in the lower-quality images that are often discarded. We present Ambient Diffusion Omni, a simple, principled framework to train diffusion models that can extract signal from all available images during training. Our framework exploits two properties of natural images -- spectral power law decay and locality. We first validate our framework by successfully training diffusion models with images synthetically corrupted by Gaussian blur, JPEG compression, and motion blur. We then use our framework to achieve state-of-the-art ImageNet FID, and we show significant improvements in both image quality and diversity for text-to-image generative modeling. The core insight is that noise dampens the initial skew between the desired high-quality distribution and the mixed distribution we actually observe. We provide rigorous theoretical justification for our approach by analyzing the trade-off between learning from biased data versus limited unbiased data across diffusion times.

Learning High-dimensional Gaussians from Censored Data

We provide efficient algorithms for the problem of distribution learning from high-dimensional Gaussian data where in each sample, some of the variable values are missing. We suppose that the variables are missing not at random (MNAR). The missingness model, denoted by $S(y)$, is the function that maps any point $y$ in $R^d$ to the subsets of its coordinates that are seen. In this work, we assume that it is known. We study the following two settings: (i) Self-censoring: An observation $x$ is generated by first sampling the true value $y$ from a $d$-dimensional Gaussian $N(\mu*, \Sigma*)$ with unknown $\mu*$ and $\Sigma*$. For each coordinate $i$, there exists a set $S_i$ subseteq $R^d$ such that $x_i = y_i$ if and only if $y_i$ in $S_i$. Otherwise, $x_i$ is missing and takes a generic value (e.g., "?"). We design an algorithm that learns $N(\mu*, \Sigma*)$ up to total variation (TV) distance epsilon, using $poly(d, 1/\epsilon)$ samples, assuming only that each pair of coordinates is observed with sufficiently high probability. (ii) Linear thresholding: An observation $x$ is generated by first sampling $y$ from a $d$-dimensional Gaussian $N(\mu*, \Sigma)$ with unknown $\mu*$ and known $\Sigma$, and then applying the missingness model $S$ where $S(y) = {i in [d] : v_i^T y <= b_i}$ for some $v_1, ..., v_d$ in $R^d$ and $b_1, ..., b_d$ in $R$. We design an efficient mean estimation algorithm, assuming that none of the possible missingness patterns is very rare conditioned on the values of the observed coordinates and that any small subset of coordinates is observed with sufficiently high probability.

Fixed Point Computation: Beating Brute Force with Smoothed Analysis

We propose a new algorithm that finds an $\varepsilon$-approximate fixed point of a smooth function from the $n$-dimensional $\ell_2$ unit ball to itself. We use the general framework of finding approximate solutions to a variational inequality, a problem that subsumes fixed point computation and the computation of a Nash Equilibrium. The algorithm's runtime is bounded by $e^{O(n)}/\varepsilon$, under the smoothed-analysis framework. This is the first known algorithm in such a generality whose runtime is faster than $(1/\varepsilon)^{O(n)}$, which is a time that suffices for an exhaustive search. We complement this result with a lower bound of $e^{\Omega(n)}$ on the query complexity for finding an $O(1)$-approximate fixed point on the unit ball, which holds even in the smoothed-analysis model, yet without the assumption that the function is smooth. Existing lower bounds are only known for the hypercube, and adapting them to the ball does not give non-trivial results even for finding $O(1/\sqrt{n})$-approximate fixed points.

Charting the Shapes of Stories with Game Theory

Stories are records of our experiences and their analysis reveals insights into the nature of being human. Successful analyses are often interdisciplinary, leveraging mathematical tools to extract structure from stories and insights from structure. Historically, these tools have been restricted to one dimensional charts and dynamic social networks; however, modern AI offers the possibility of identifying more fully the plot structure, character incentives, and, importantly, counterfactual plot lines that the story could have taken but did not take. In this work, we use AI to model the structure of stories as game-theoretic objects, amenable to quantitative analysis. This allows us to not only interrogate each character's decision making, but also possibly peer into the original author's conception of the characters' world. We demonstrate our proposed technique on Shakespeare's famous Romeo and Juliet. We conclude with a discussion of how our analysis could be replicated in broader contexts, including real-life scenarios.

How much is a noisy image worth? Data Scaling Laws for Ambient Diffusion

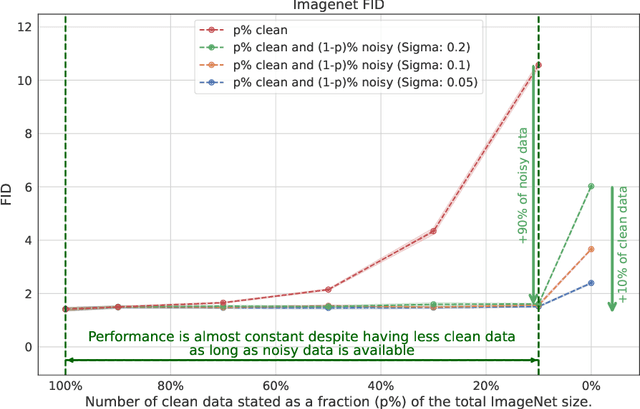
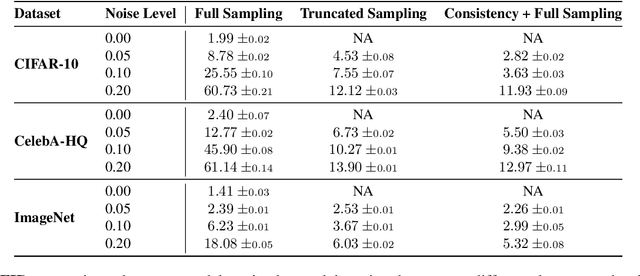
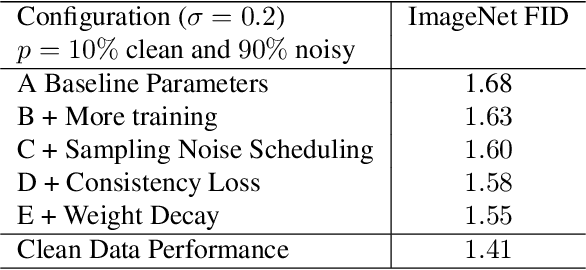
The quality of generative models depends on the quality of the data they are trained on. Creating large-scale, high-quality datasets is often expensive and sometimes impossible, e.g. in certain scientific applications where there is no access to clean data due to physical or instrumentation constraints. Ambient Diffusion and related frameworks train diffusion models with solely corrupted data (which are usually cheaper to acquire) but ambient models significantly underperform models trained on clean data. We study this phenomenon at scale by training more than $80$ models on data with different corruption levels across three datasets ranging from $30,000$ to $\approx 1.3$M samples. We show that it is impossible, at these sample sizes, to match the performance of models trained on clean data when only training on noisy data. Yet, a combination of a small set of clean data (e.g.~$10\%$ of the total dataset) and a large set of highly noisy data suffices to reach the performance of models trained solely on similar-size datasets of clean data, and in particular to achieve near state-of-the-art performance. We provide theoretical evidence for our findings by developing novel sample complexity bounds for learning from Gaussian Mixtures with heterogeneous variances. Our theoretical model suggests that, for large enough datasets, the effective marginal utility of a noisy sample is exponentially worse than that of a clean sample. Providing a small set of clean samples can significantly reduce the sample size requirements for noisy data, as we also observe in our experiments.

Maximizing utility in multi-agent environments by anticipating the behavior of other learners

Learning algorithms are often used to make decisions in sequential decision-making environments. In multi-agent settings, the decisions of each agent can affect the utilities/losses of the other agents. Therefore, if an agent is good at anticipating the behavior of the other agents, in particular how they will make decisions in each round as a function of their experience that far, it could try to judiciously make its own decisions over the rounds of the interaction so as to influence the other agents to behave in a way that ultimately benefits its own utility. In this paper, we study repeated two-player games involving two types of agents: a learner, which employs an online learning algorithm to choose its strategy in each round; and an optimizer, which knows the learner's utility function and the learner's online learning algorithm. The optimizer wants to plan ahead to maximize its own utility, while taking into account the learner's behavior. We provide two results: a positive result for repeated zero-sum games and a negative result for repeated general-sum games. Our positive result is an algorithm for the optimizer, which exactly maximizes its utility against a learner that plays the Replicator Dynamics -- the continuous-time analogue of Multiplicative Weights Update (MWU). Additionally, we use this result to provide an algorithm for the optimizer against MWU, i.e.~for the discrete-time setting, which guarantees an average utility for the optimizer that is higher than the value of the one-shot game. Our negative result shows that, unless P=NP, there is no Fully Polynomial Time Approximation Scheme (FPTAS) for maximizing the utility of an optimizer against a learner that best-responds to the history in each round. Yet, this still leaves open the question of whether there exists a polynomial-time algorithm that optimizes the utility up to $o(T)$.