Charting the Shapes of Stories with Game Theory

Stories are records of our experiences and their analysis reveals insights into the nature of being human. Successful analyses are often interdisciplinary, leveraging mathematical tools to extract structure from stories and insights from structure. Historically, these tools have been restricted to one dimensional charts and dynamic social networks; however, modern AI offers the possibility of identifying more fully the plot structure, character incentives, and, importantly, counterfactual plot lines that the story could have taken but did not take. In this work, we use AI to model the structure of stories as game-theoretic objects, amenable to quantitative analysis. This allows us to not only interrogate each character's decision making, but also possibly peer into the original author's conception of the characters' world. We demonstrate our proposed technique on Shakespeare's famous Romeo and Juliet. We conclude with a discussion of how our analysis could be replicated in broader contexts, including real-life scenarios.

On Diffusion Models for Multi-Agent Partial Observability: Shared Attractors, Error Bounds, and Composite Flow

Multiagent systems grapple with partial observability (PO), and the decentralized POMDP (Dec-POMDP) model highlights the fundamental nature of this challenge. Whereas recent approaches to address PO have appealed to deep learning models, providing a rigorous understanding of how these models and their approximation errors affect agents' handling of PO and their interactions remain a challenge. In addressing this challenge, we investigate reconstructing global states from local action-observation histories in Dec-POMDPs using diffusion models. We first find that diffusion models conditioned on local history represent possible states as stable fixed points. In collectively observable (CO) Dec-POMDPs, individual diffusion models conditioned on agents' local histories share a unique fixed point corresponding to the global state, while in non-CO settings, the shared fixed points yield a distribution of possible states given joint history. We further find that, with deep learning approximation errors, fixed points can deviate from true states and the deviation is negatively correlated to the Jacobian rank. Inspired by this low-rank property, we bound the deviation by constructing a surrogate linear regression model that approximates the local behavior of diffusion models. With this bound, we propose a composite diffusion process iterating over agents with theoretical convergence guarantees to the true state.

GemNet: Menu-Based, Strategy-Proof Multi-Bidder Auctions Through Deep Learning

Differentiable economics uses deep learning for automated mechanism design. Despite strong progress, it has remained an open problem to learn multi-bidder, general, and fully strategy-proof (SP) auctions. We introduce GEneral Menu-based NETwork (GemNet), which significantly extends the menu-based approach of RochetNet [D\"utting et al., 2023] to the multi-bidder setting. The challenge in achieving SP is to learn bidder-independent menus that are feasible, so that the optimal menu choices for each bidder do not over-allocate items when taken together (we call this menu compatibility). GemNet penalizes the failure of menu compatibility during training, and transforms learned menus after training through price changes, by considering a set of discretized bidder values and reasoning about Lipschitz smoothness to guarantee menu compatibility on the entire value space. This approach is general, leaving undisturbed trained menus that already satisfy menu compatibility and reducing to RochetNet for a single bidder. Mixed-integer linear programs are used for menu transforms and through a number of optimizations, including adaptive grids and methods to skip menu elements, we scale to large auction design problems. GemNet learns auctions with better revenue than affine maximization methods, achieves exact SP whereas previous general multi-bidder methods are approximately SP, and offers greatly enhanced interpretability.

Data Market Design through Deep Learning

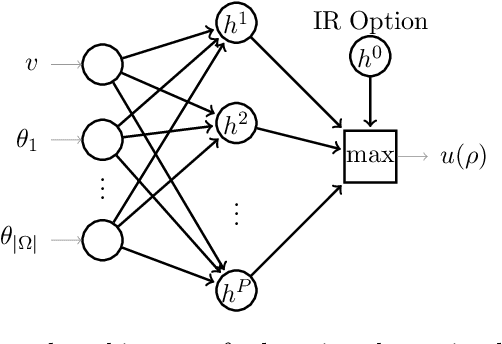
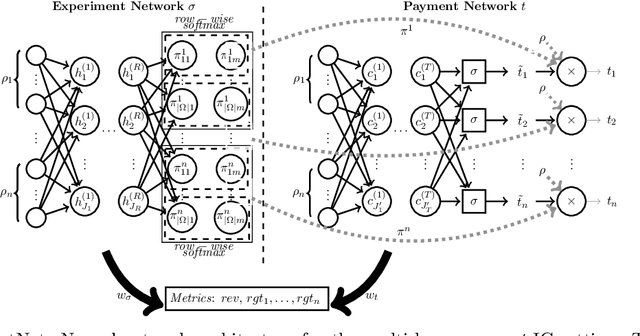
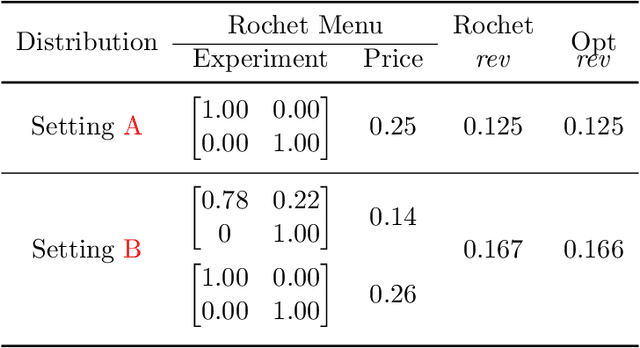
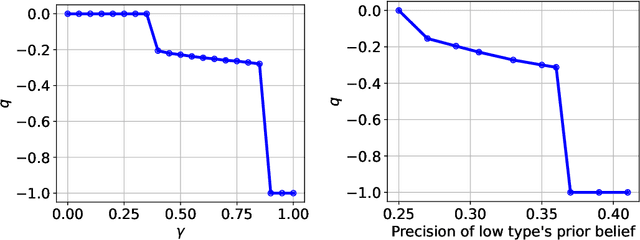
The $\textit{data market design}$ problem is a problem in economic theory to find a set of signaling schemes (statistical experiments) to maximize expected revenue to the information seller, where each experiment reveals some of the information known to a seller and has a corresponding price [Bergemann et al., 2018]. Each buyer has their own decision to make in a world environment, and their subjective expected value for the information associated with a particular experiment comes from the improvement in this decision and depends on their prior and value for different outcomes. In a setting with multiple buyers, a buyer's expected value for an experiment may also depend on the information sold to others [Bonatti et al., 2022]. We introduce the application of deep learning for the design of revenue-optimal data markets, looking to expand the frontiers of what can be understood and achieved. Relative to earlier work on deep learning for auction design [D\"utting et al., 2023], we must learn signaling schemes rather than allocation rules and handle $\textit{obedience constraints}$ $-$ these arising from modeling the downstream actions of buyers $-$ in addition to incentive constraints on bids. Our experiments demonstrate that this new deep learning framework can almost precisely replicate all known solutions from theory, expand to more complex settings, and be used to establish the optimality of new designs for data markets and make conjectures in regard to the structure of optimal designs.