Charting the Shapes of Stories with Game Theory

Stories are records of our experiences and their analysis reveals insights into the nature of being human. Successful analyses are often interdisciplinary, leveraging mathematical tools to extract structure from stories and insights from structure. Historically, these tools have been restricted to one dimensional charts and dynamic social networks; however, modern AI offers the possibility of identifying more fully the plot structure, character incentives, and, importantly, counterfactual plot lines that the story could have taken but did not take. In this work, we use AI to model the structure of stories as game-theoretic objects, amenable to quantitative analysis. This allows us to not only interrogate each character's decision making, but also possibly peer into the original author's conception of the characters' world. We demonstrate our proposed technique on Shakespeare's famous Romeo and Juliet. We conclude with a discussion of how our analysis could be replicated in broader contexts, including real-life scenarios.

Procurement Auctions via Approximately Optimal Submodular Optimization

We study procurement auctions, where an auctioneer seeks to acquire services from strategic sellers with private costs. The quality of services is measured by a submodular function known to the auctioneer. Our goal is to design computationally efficient procurement auctions that (approximately) maximize the difference between the quality of the acquired services and the total cost of the sellers, while ensuring incentive compatibility (IC), individual rationality (IR) for sellers, and non-negative surplus (NAS) for the auctioneer. Our contributions are twofold: (i) we provide an improved analysis of existing algorithms for non-positive submodular function maximization, and (ii) we design efficient frameworks that transform submodular optimization algorithms into mechanisms that are IC, IR, NAS, and approximation-preserving. These frameworks apply to both the offline setting, where all sellers' bids and services are available simultaneously, and the online setting, where sellers arrive in an adversarial order, requiring the auctioneer to make irrevocable decisions. We also explore whether state-of-the-art submodular optimization algorithms can be converted into descending auctions in adversarial settings, where the schedule of descending prices is determined by an adversary. We show that a submodular optimization algorithm satisfying bi-criteria $(1/2, 1)$-approximation in welfare can be effectively adapted to a descending auction. Additionally, we establish a connection between descending auctions and online submodular optimization. Finally, we demonstrate the practical applications of our frameworks by instantiating them with state-of-the-art submodular optimization algorithms and empirically comparing their welfare performance on publicly available datasets with thousands of sellers.

Bandits with Deterministically Evolving States

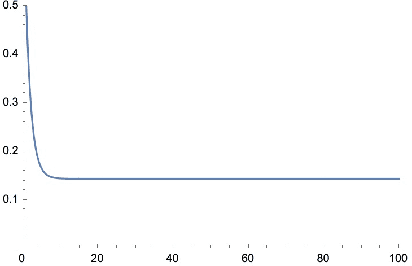
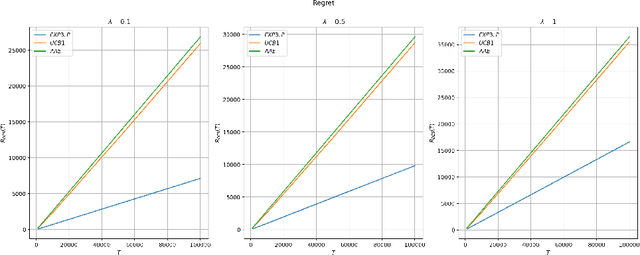
We propose a model for learning with bandit feedback while accounting for deterministically evolving and unobservable states that we call Bandits with Deterministically Evolving States. The workhorse applications of our model are learning for recommendation systems and learning for online ads. In both cases, the reward that the algorithm obtains at each round is a function of the short-term reward of the action chosen and how ``healthy'' the system is (i.e., as measured by its state). For example, in recommendation systems, the reward that the platform obtains from a user's engagement with a particular type of content depends not only on the inherent features of the specific content, but also on how the user's preferences have evolved as a result of interacting with other types of content on the platform. Our general model accounts for the different rate $\lambda \in [0,1]$ at which the state evolves (e.g., how fast a user's preferences shift as a result of previous content consumption) and encompasses standard multi-armed bandits as a special case. The goal of the algorithm is to minimize a notion of regret against the best-fixed sequence of arms pulled. We analyze online learning algorithms for any possible parametrization of the evolution rate $\lambda$. Specifically, the regret rates obtained are: for $\lambda \in [0, 1/T^2]$: $\widetilde O(\sqrt{KT})$; for $\lambda = T^{-a/b}$ with $b < a < 2b$: $\widetilde O (T^{b/a})$; for $\lambda \in (1/T, 1 - 1/\sqrt{T}): \widetilde O (K^{1/3}T^{2/3})$; and for $\lambda \in [1 - 1/\sqrt{T}, 1]: \widetilde O (K\sqrt{T})$.

U-Calibration: Forecasting for an Unknown Agent

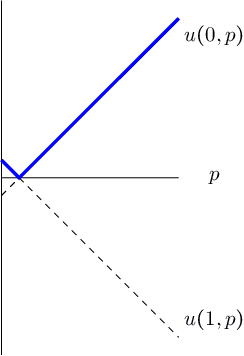
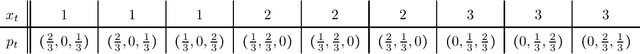
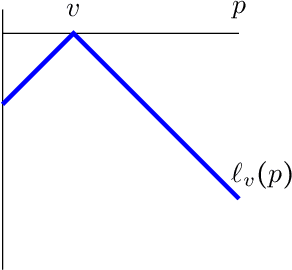
We consider the problem of evaluating forecasts of binary events whose predictions are consumed by rational agents who take an action in response to a prediction, but whose utility is unknown to the forecaster. We show that optimizing forecasts for a single scoring rule (e.g., the Brier score) cannot guarantee low regret for all possible agents. In contrast, forecasts that are well-calibrated guarantee that all agents incur sublinear regret. However, calibration is not a necessary criterion here (it is possible for miscalibrated forecasts to provide good regret guarantees for all possible agents), and calibrated forecasting procedures have provably worse convergence rates than forecasting procedures targeting a single scoring rule. Motivated by this, we present a new metric for evaluating forecasts that we call U-calibration, equal to the maximal regret of the sequence of forecasts when evaluated under any bounded scoring rule. We show that sublinear U-calibration error is a necessary and sufficient condition for all agents to achieve sublinear regret guarantees. We additionally demonstrate how to compute the U-calibration error efficiently and provide an online algorithm that achieves $O(\sqrt{T})$ U-calibration error (on par with optimal rates for optimizing for a single scoring rule, and bypassing lower bounds for the traditionally calibrated learning procedures). Finally, we discuss generalizations to the multiclass prediction setting.

Corruption-Robust Contextual Search through Density Updates

We study the problem of contextual search in the adversarial noise model. Let $d$ be the dimension of the problem, $T$ be the time horizon and $C$ be the total amount of noise in the system. For the $\eps$-ball loss, we give a tight regret bound of $O(C + d \log(1/\eps))$ improving over the $O(d^3 \log(1/\eps)) \log^2(T) + C \log(T) \log(1/\eps))$ bound of Krishnamurthy et al (STOC21). For the symmetric loss, we give an efficient algorithm with regret $O(C+d \log T)$. Our techniques are a significant departure from prior approaches. Specifically, we keep track of density functions over the candidate vectors instead of a knowledge set consisting of the candidate vectors consistent with the feedback obtained.

Contextual Recommendations and Low-Regret Cutting-Plane Algorithms

We consider the following variant of contextual linear bandits motivated by routing applications in navigational engines and recommendation systems. We wish to learn a hidden $d$-dimensional value $w^*$. Every round, we are presented with a subset $\mathcal{X}_t \subseteq \mathbb{R}^d$ of possible actions. If we choose (i.e. recommend to the user) action $x_t$, we obtain utility $\langle x_t, w^* \rangle$ but only learn the identity of the best action $\arg\max_{x \in \mathcal{X}_t} \langle x, w^* \rangle$. We design algorithms for this problem which achieve regret $O(d\log T)$ and $\exp(O(d \log d))$. To accomplish this, we design novel cutting-plane algorithms with low "regret" -- the total distance between the true point $w^*$ and the hyperplanes the separation oracle returns. We also consider the variant where we are allowed to provide a list of several recommendations. In this variant, we give an algorithm with $O(d^2 \log d)$ regret and list size $\mathrm{poly}(d)$. Finally, we construct nearly tight algorithms for a weaker variant of this problem where the learner only learns the identity of an action that is better than the recommendation. Our results rely on new algorithmic techniques in convex geometry (including a variant of Steiner's formula for the centroid of a convex set) which may be of independent interest.

Learning to Price Against a Moving Target

In the Learning to Price setting, a seller posts prices over time with the goal of maximizing revenue while learning the buyer's valuation. This problem is very well understood when values are stationary (fixed or iid). Here we study the problem where the buyer's value is a moving target, i.e., they change over time either by a stochastic process or adversarially with bounded variation. In either case, we provide matching upper and lower bounds on the optimal revenue loss. Since the target is moving, any information learned soon becomes out-dated, which forces the algorithms to keep switching between exploring and exploiting phases.

Bandits with adversarial scaling

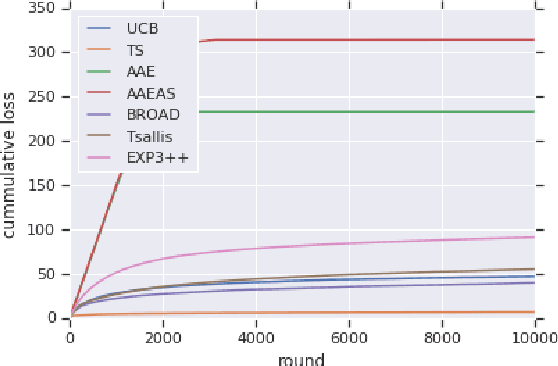
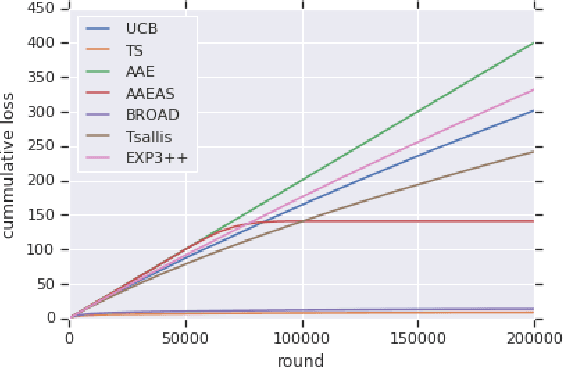
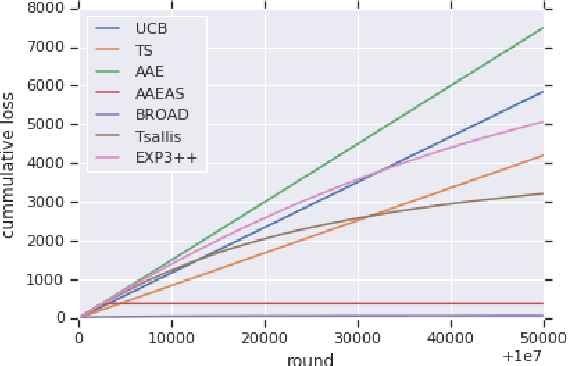
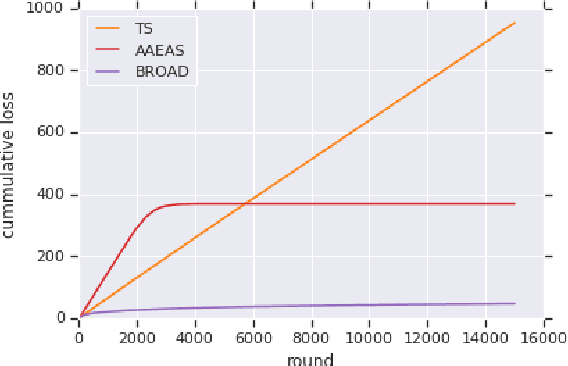
We study "adversarial scaling", a multi-armed bandit model where rewards have a stochastic and an adversarial component. Our model captures display advertising where the "click-through-rate" can be decomposed to a (fixed across time) arm-quality component and a non-stochastic user-relevance component (fixed across arms). Despite the relative stochasticity of our model, we demonstrate two settings where most bandit algorithms suffer. On the positive side, we show that two algorithms, one from the action elimination and one from the mirror descent family are adaptive enough to be robust to adversarial scaling. Our results shed light on the robustness of adaptive parameter selection in stochastic bandits, which may be of independent interest.

Contextual Search for General Hypothesis Classes

We study a general version of the problem of online learning under binary feedback: there is a hidden function $f : \mathcal{X} \rightarrow \mathcal{Y}$ in a certain hypothesis class $\mathcal{H}$. A learner is given adversarially chosen inputs (contexts) $x_t \in \mathcal{X}$ and is asked to submit a guess $y_t \in \mathcal{Y}$ for the value $f(x_t)$. Upon guessing the learner incurs a certain loss $L(y_t, f(x_t))$ and learns whether $y_t \leq f(x_t)$ or $y_t > f(x_t)$. The special case where $\mathcal{H}$ is the class of linear functions over the unit ball has been studied in a series of papers. We both generalize and improve these results. We provide a $O(d^2)$ regret bound where $d$ is the covering dimension of the hypothesis class. The algorithms are based on a novel technique which we call Steiner potential since in the linear case it reduces to controlling the value of the Steiner polynomial of a convex region at various scales. We also show that this new technique provides optimal regret (up to log factors) in the linear case (i.e. the original contextual search problem), improving the previously known bound of $O(d^4)$ to $O(d \log d)$. Finally, we extend these results to a noisy feedback model, where each round our feedback is flipped with fixed probability $p < 1/2$.

Learning to Clear the Market

The problem of market clearing is to set a price for an item such that quantity demanded equals quantity supplied. In this work, we cast the problem of predicting clearing prices into a learning framework and use the resulting models to perform revenue optimization in auctions and markets with contextual information. The economic intuition behind market clearing allows us to obtain fine-grained control over the aggressiveness of the resulting pricing policy, grounded in theory. To evaluate our approach, we fit a model of clearing prices over a massive dataset of bids in display ad auctions from a major ad exchange. The learned prices outperform other modeling techniques in the literature in terms of revenue and efficiency trade-offs. Because of the convex nature of the clearing loss function, the convergence rate of our method is as fast as linear regression.