Efficient Online Conformal Selection with Limited Feedback

We address the problem of conformal selection, where an agent must select a minimal subset of options to ensure that at least one ``success'' is identified with a pre-specified target probability $φ$. While traditional online conformal prediction focuses on maintaining validity for the observed sequence, minimizing the resource cost (efficiency) of such selections, especially under limited feedback, remains a significant challenge. In this work, we consider settings with the most limited ``bandit'' feedback, and demonstrate that the simple Adaptive Conformal Inference (ACI) update rule, when applied to the appropriate control parameter or dual variable, is both adversarially valid, ensuring the success target is met on average for any input sequence (and hence under distribution shifts), and stochastically efficient, achieving sublinear efficiency regret for $i.i.d.$ inputs against an appropriate stochastic benchmark. We show such guarantees under canonical models capturing bandit and semi-bandit feedback to the agent via a unifying algorithmic technique, and analytic framework involving Lyapunov functions. Our approach handles more complex settings than prior work, while requiring significantly less feedback, and our results provide a new theoretical bridge between efficient online learning with limited feedback and distribution-free uncertainty quantification.

Compact Conformal Subgraphs

Conformal prediction provides rigorous, distribution-free uncertainty guarantees, but often yields prohibitively large prediction sets in structured domains such as routing, planning, or sequential recommendation. We introduce "graph-based conformal compression", a framework for constructing compact subgraphs that preserve statistical validity while reducing structural complexity. We formulate compression as selecting a smallest subgraph capturing a prescribed fraction of the probability mass, and reduce to a weighted version of densest $k$-subgraphs in hypergraphs, in the regime where the subgraph has a large fraction of edges. We design efficient approximation algorithms that achieve constant factor coverage and size trade-offs. Crucially, we prove that our relaxation satisfies a monotonicity property, derived from a connection to parametric minimum cuts, which guarantees the nestedness required for valid conformal guarantees. Our results on the one hand bridge efficient conformal prediction with combinatorial graph compression via monotonicity, to provide rigorous guarantees on both statistical validity, and compression or size. On the other hand, they also highlight an algorithmic regime, distinct from classical densest-$k$-subgraph hardness settings, where the problem can be approximated efficiently. We finally validate our algorithmic approach via simulations for trip planning and navigation, and compare to natural baselines.

When Are Two Lists Better than One?: Benefits and Harms in Joint Decision-making

Historically, much of machine learning research has focused on the performance of the algorithm alone, but recently more attention has been focused on optimizing joint human-algorithm performance. Here, we analyze a specific type of human-algorithm collaboration where the algorithm has access to a set of $n$ items, and presents a subset of size $k$ to the human, who selects a final item from among those $k$. This scenario could model content recommendation, route planning, or any type of labeling task. Because both the human and algorithm have imperfect, noisy information about the true ordering of items, the key question is: which value of $k$ maximizes the probability that the best item will be ultimately selected? For $k=1$, performance is optimized by the algorithm acting alone, and for $k=n$ it is optimized by the human acting alone. Surprisingly, we show that for multiple of noise models, it is optimal to set $k \in [2, n-1]$ - that is, there are strict benefits to collaborating, even when the human and algorithm have equal accuracy separately. We demonstrate this theoretically for the Mallows model and experimentally for the Random Utilities models of noisy permutations. However, we show this pattern is reversed when the human is anchored on the algorithm's presented ordering - the joint system always has strictly worse performance. We extend these results to the case where the human and algorithm differ in their accuracy levels, showing that there always exist regimes where a more accurate agent would strictly benefit from collaborating with a less accurate one, but these regimes are asymmetric between the human and the algorithm's accuracy.

Congested Bandits: Optimal Routing via Short-term Resets

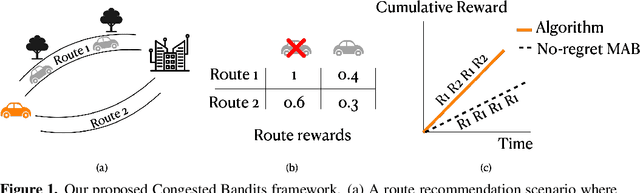
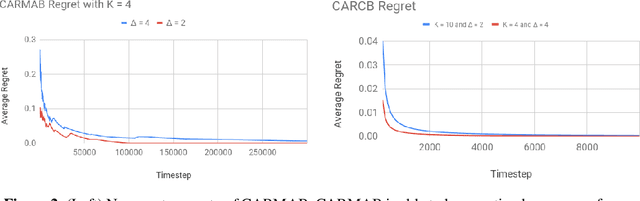
For traffic routing platforms, the choice of which route to recommend to a user depends on the congestion on these routes -- indeed, an individual's utility depends on the number of people using the recommended route at that instance. Motivated by this, we introduce the problem of Congested Bandits where each arm's reward is allowed to depend on the number of times it was played in the past $\Delta$ timesteps. This dependence on past history of actions leads to a dynamical system where an algorithm's present choices also affect its future pay-offs, and requires an algorithm to plan for this. We study the congestion aware formulation in the multi-armed bandit (MAB) setup and in the contextual bandit setup with linear rewards. For the multi-armed setup, we propose a UCB style algorithm and show that its policy regret scales as $\tilde{O}(\sqrt{K \Delta T})$. For the linear contextual bandit setup, our algorithm, based on an iterative least squares planner, achieves policy regret $\tilde{O}(\sqrt{dT} + \Delta)$. From an experimental standpoint, we corroborate the no-regret properties of our algorithms via a simulation study.

Online Learning and Bandits with Queried Hints

We consider the classic online learning and stochastic multi-armed bandit (MAB) problems, when at each step, the online policy can probe and find out which of a small number ($k$) of choices has better reward (or loss) before making its choice. In this model, we derive algorithms whose regret bounds have exponentially better dependence on the time horizon compared to the classic regret bounds. In particular, we show that probing with $k=2$ suffices to achieve time-independent regret bounds for online linear and convex optimization. The same number of probes improve the regret bound of stochastic MAB with independent arms from $O(\sqrt{nT})$ to $O(n^2 \log T)$, where $n$ is the number of arms and $T$ is the horizon length. For stochastic MAB, we also consider a stronger model where a probe reveals the reward values of the probed arms, and show that in this case, $k=3$ probes suffice to achieve parameter-independent constant regret, $O(n^2)$. Such regret bounds cannot be achieved even with full feedback after the play, showcasing the power of limited ``advice'' via probing before making the play. We also present extensions to the setting where the hints can be imperfect, and to the case of stochastic MAB where the rewards of the arms can be correlated.

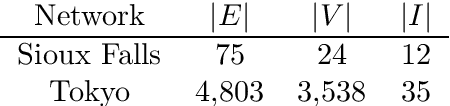
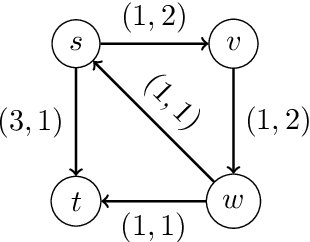
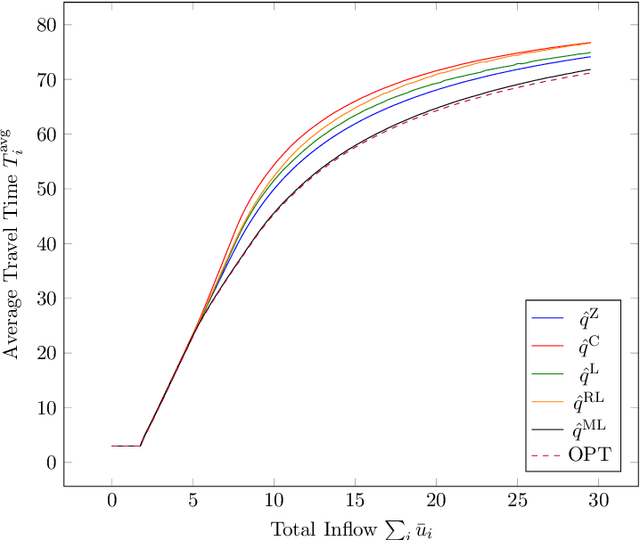
Machine-Learned Prediction Equilibrium for Dynamic Traffic Assignment

We study a dynamic traffic assignment model, where agents base their instantaneous routing decisions on real-time delay predictions. We formulate a mathematically concise model and derive properties of the predictors that ensure a dynamic prediction equilibrium exists. We demonstrate the versatility of our framework by showing that it subsumes the well-known full information and instantaneous information models, in addition to admitting further realistic predictors as special cases. We complement our theoretical analysis by an experimental study, in which we systematically compare the induced average travel times of different predictors, including a machine-learning model trained on data gained from previously computed equilibrium flows, both on a synthetic and a real road network.

Contextual Recommendations and Low-Regret Cutting-Plane Algorithms

We consider the following variant of contextual linear bandits motivated by routing applications in navigational engines and recommendation systems. We wish to learn a hidden $d$-dimensional value $w^*$. Every round, we are presented with a subset $\mathcal{X}_t \subseteq \mathbb{R}^d$ of possible actions. If we choose (i.e. recommend to the user) action $x_t$, we obtain utility $\langle x_t, w^* \rangle$ but only learn the identity of the best action $\arg\max_{x \in \mathcal{X}_t} \langle x, w^* \rangle$. We design algorithms for this problem which achieve regret $O(d\log T)$ and $\exp(O(d \log d))$. To accomplish this, we design novel cutting-plane algorithms with low "regret" -- the total distance between the true point $w^*$ and the hyperplanes the separation oracle returns. We also consider the variant where we are allowed to provide a list of several recommendations. In this variant, we give an algorithm with $O(d^2 \log d)$ regret and list size $\mathrm{poly}(d)$. Finally, we construct nearly tight algorithms for a weaker variant of this problem where the learner only learns the identity of an action that is better than the recommendation. Our results rely on new algorithmic techniques in convex geometry (including a variant of Steiner's formula for the centroid of a convex set) which may be of independent interest.