Binary Search with Distributional Predictions

Algorithms with (machine-learned) predictions is a powerful framework for combining traditional worst-case algorithms with modern machine learning. However, the vast majority of work in this space assumes that the prediction itself is non-probabilistic, even if it is generated by some stochastic process (such as a machine learning system). This is a poor fit for modern ML, particularly modern neural networks, which naturally generate a distribution. We initiate the study of algorithms with distributional predictions, where the prediction itself is a distribution. We focus on one of the simplest yet fundamental settings: binary search (or searching a sorted array). This setting has one of the simplest algorithms with a point prediction, but what happens if the prediction is a distribution? We show that this is a richer setting: there are simple distributions where using the classical prediction-based algorithm with any single prediction does poorly. Motivated by this, as our main result, we give an algorithm with query complexity $O(H(p) + \log \eta)$, where $H(p)$ is the entropy of the true distribution $p$ and $\eta$ is the earth mover's distance between $p$ and the predicted distribution $\hat p$. This also yields the first distributionally-robust algorithm for the classical problem of computing an optimal binary search tree given a distribution over target keys. We complement this with a lower bound showing that this query complexity is essentially optimal (up to constants), and experiments validating the practical usefulness of our algorithm.

Online Dynamic Acknowledgement with Learned Predictions

We revisit the online dynamic acknowledgment problem. In the problem, a sequence of requests arrive over time to be acknowledged, and all outstanding requests can be satisfied simultaneously by one acknowledgement. The goal of the problem is to minimize the total request delay plus acknowledgement cost. This elegant model studies the trade-off between acknowledgement cost and waiting experienced by requests. The problem has been well studied and the tight competitive ratios have been determined. For this well-studied problem, we focus on how to effectively use machine-learned predictions to have better performance. We develop algorithms that perform arbitrarily close to the optimum with accurate predictions while concurrently having the guarantees arbitrarily close to what the best online algorithms can offer without access to predictions, thereby achieving simultaneous optimum consistency and robustness. This new result is enabled by our novel prediction error measure. No error measure was defined for the problem prior to our work, and natural measures failed due to the challenge that requests with different arrival times have different effects on the objective. We hope our ideas can be used for other online problems with temporal aspects that have been resisting proper error measures.

Online Learning and Bandits with Queried Hints

We consider the classic online learning and stochastic multi-armed bandit (MAB) problems, when at each step, the online policy can probe and find out which of a small number ($k$) of choices has better reward (or loss) before making its choice. In this model, we derive algorithms whose regret bounds have exponentially better dependence on the time horizon compared to the classic regret bounds. In particular, we show that probing with $k=2$ suffices to achieve time-independent regret bounds for online linear and convex optimization. The same number of probes improve the regret bound of stochastic MAB with independent arms from $O(\sqrt{nT})$ to $O(n^2 \log T)$, where $n$ is the number of arms and $T$ is the horizon length. For stochastic MAB, we also consider a stronger model where a probe reveals the reward values of the probed arms, and show that in this case, $k=3$ probes suffice to achieve parameter-independent constant regret, $O(n^2)$. Such regret bounds cannot be achieved even with full feedback after the play, showcasing the power of limited ``advice'' via probing before making the play. We also present extensions to the setting where the hints can be imperfect, and to the case of stochastic MAB where the rewards of the arms can be correlated.

Parsimonious Learning-Augmented Caching

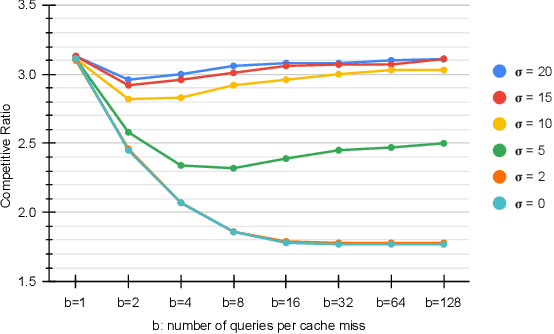
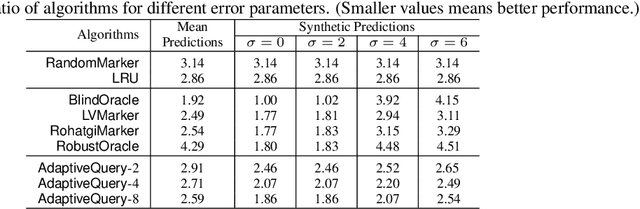
Learning-augmented algorithms -- in which, traditional algorithms are augmented with machine-learned predictions -- have emerged as a framework to go beyond worst-case analysis. The overarching goal is to design algorithms that perform near-optimally when the predictions are accurate yet retain certain worst-case guarantees irrespective of the accuracy of the predictions. This framework has been successfully applied to online problems such as caching where the predictions can be used to alleviate uncertainties. In this paper we introduce and study the setting in which the learning-augmented algorithm can utilize the predictions parsimoniously. We consider the caching problem -- which has been extensively studied in the learning-augmented setting -- and show that one can achieve quantitatively similar results but only using a sublinear number of predictions.

Faster Matchings via Learned Duals

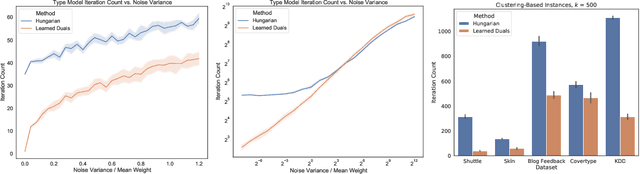
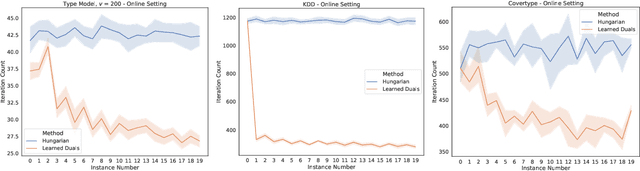
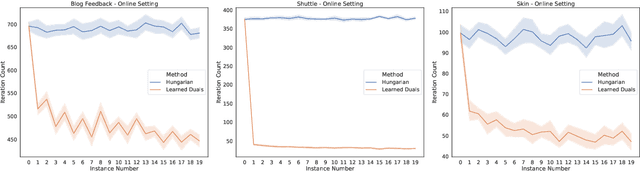
A recent line of research investigates how algorithms can be augmented with machine-learned predictions to overcome worst case lower bounds. This area has revealed interesting algorithmic insights into problems, with particular success in the design of competitive online algorithms. However, the question of improving algorithm running times with predictions has largely been unexplored. We take a first step in this direction by combining the idea of machine-learned predictions with the idea of "warm-starting" primal-dual algorithms. We consider one of the most important primitives in combinatorial optimization: weighted bipartite matching and its generalization to $b$-matching. We identify three key challenges when using learned dual variables in a primal-dual algorithm. First, predicted duals may be infeasible, so we give an algorithm that efficiently maps predicted infeasible duals to nearby feasible solutions. Second, once the duals are feasible, they may not be optimal, so we show that they can be used to quickly find an optimal solution. Finally, such predictions are useful only if they can be learned, so we show that the problem of learning duals for matching has low sample complexity. We validate our theoretical findings through experiments on both real and synthetic data. As a result we give a rigorous, practical, and empirically effective method to compute bipartite matchings.

A Relational Gradient Descent Algorithm For Support Vector Machine Training

We consider gradient descent like algorithms for Support Vector Machine (SVM) training when the data is in relational form. The gradient of the SVM objective can not be efficiently computed by known techniques as it suffers from the ``subtraction problem''. We first show that the subtraction problem can not be surmounted by showing that computing any constant approximation of the gradient of the SVM objective function is $\#P$-hard, even for acyclic joins. We, however, circumvent the subtraction problem by restricting our attention to stable instances, which intuitively are instances where a nearly optimal solution remains nearly optimal if the points are perturbed slightly. We give an efficient algorithm that computes a ``pseudo-gradient'' that guarantees convergence for stable instances at a rate comparable to that achieved by using the actual gradient. We believe that our results suggest that this sort of stability the analysis would likely yield useful insight in the context of designing algorithms on relational data for other learning problems in which the subtraction problem arises.

Approximate Aggregate Queries Under Additive Inequalities

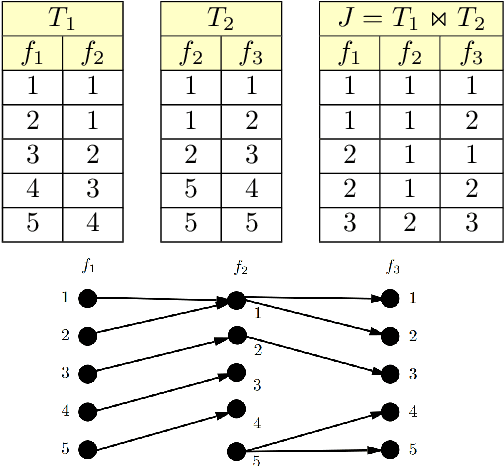
We consider the problem of evaluating certain types of functional aggregation queries on relational data subject to additive inequalities. Such aggregation queries, with a smallish number of additive inequalities, arise naturally/commonly in many applications, particularly in learning applications. We give a relatively complete categorization of the computational complexity of such problems. We first show that the problem is NP-hard, even in the case of one additive inequality. Thus we turn to approximating the query. Our main result is an efficient algorithm for approximating, with arbitrarily small relative error, many natural aggregation queries with one additive inequality. We give examples of natural queries that can be efficiently solved using this algorithm. In contrast, we show that the situation with two additive inequalities is quite different, by showing that it is NP-hard to evaluate simple aggregation queries, with two additive inequalities, with any bounded relative error.

On Coresets for Regularized Loss Minimization

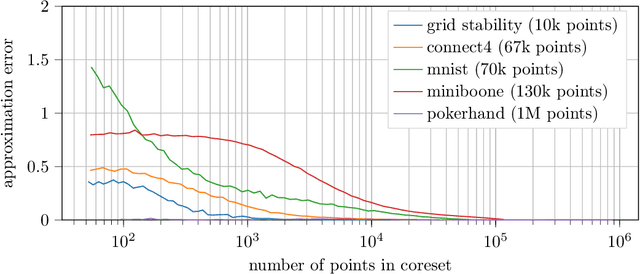
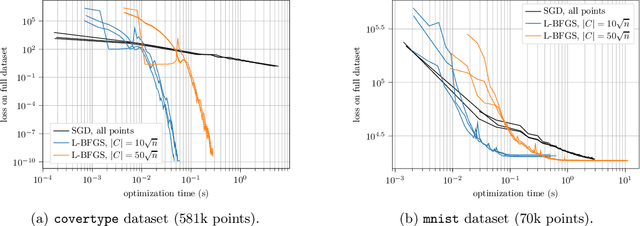
We design and mathematically analyze sampling-based algorithms for regularized loss minimization problems that are implementable in popular computational models for large data, in which the access to the data is restricted in some way. Our main result is that if the regularizer's effect does not become negligible as the norm of the hypothesis scales, and as the data scales, then a uniform sample of modest size is with high probability a coreset. In the case that the loss function is either logistic regression or soft-margin support vector machines, and the regularizer is one of the common recommended choices, this result implies that a uniform sample of size $O(d \sqrt{n})$ is with high probability a coreset of $n$ points in $\Re^d$. We contrast this upper bound with two lower bounds. The first lower bound shows that our analysis of uniform sampling is tight; that is, a smaller uniform sample will likely not be a core set. The second lower bound shows that in some sense uniform sampling is close to optimal, as significantly smaller core sets do not generally exist.