Kirk Pruhs
Relational Boosted Regression Trees
Jul 25, 2021Abstract:Many tasks use data housed in relational databases to train boosted regression tree models. In this paper, we give a relational adaptation of the greedy algorithm for training boosted regression trees. For the subproblem of calculating the sum of squared residuals of the dataset, which dominates the runtime of the boosting algorithm, we provide a $(1 + \epsilon)$-approximation using the tensor sketch technique. Employing this approximation within the relational boosted regression trees algorithm leads to learning similar model parameters, but with asymptotically better runtime.
Relational Algorithms for k-means Clustering
Aug 01, 2020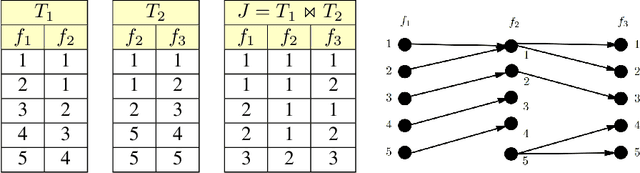
Abstract:The majority of learning tasks faced by data scientists involve relational data, yet most standard algorithms for standard learning problems are not designed to accept relational data as input. The standard practice to address this issue is to join the relational data to create the type of geometric input that standard learning algorithms expect. Unfortunately, this standard practice has exponential worst-case time and space complexity. This leads us to consider what we call the Relational Learning Question: ``Which standard learning algorithms can be efficiently implemented on relational data, and for those that can not, is there an alternative algorithm that can be efficiently implemented on relational data and that has similar performance guarantees to the standard algorithm?'' In this paper, we address the relational learning question for two well-known algorithms for the standard $k$-means clustering problem. We first show that the $k$-means++ algorithm can be efficiently implemented on relational data. In contrast, we show that the adaptive $k$-means algorithm likely can not be efficiently implemented on relational data, as this would imply $P = \#P$. However, we show that a slight variation of this adaptive $k$-means algorithm can be efficiently implemented on relational data, and that this alternative algorithm has the same performance guarantee as the original algorithm, that is that it outputs an $O(1)$-approximate sketch.
A Relational Gradient Descent Algorithm For Support Vector Machine Training
May 11, 2020Abstract:We consider gradient descent like algorithms for Support Vector Machine (SVM) training when the data is in relational form. The gradient of the SVM objective can not be efficiently computed by known techniques as it suffers from the ``subtraction problem''. We first show that the subtraction problem can not be surmounted by showing that computing any constant approximation of the gradient of the SVM objective function is $\#P$-hard, even for acyclic joins. We, however, circumvent the subtraction problem by restricting our attention to stable instances, which intuitively are instances where a nearly optimal solution remains nearly optimal if the points are perturbed slightly. We give an efficient algorithm that computes a ``pseudo-gradient'' that guarantees convergence for stable instances at a rate comparable to that achieved by using the actual gradient. We believe that our results suggest that this sort of stability the analysis would likely yield useful insight in the context of designing algorithms on relational data for other learning problems in which the subtraction problem arises.
Approximate Aggregate Queries Under Additive Inequalities
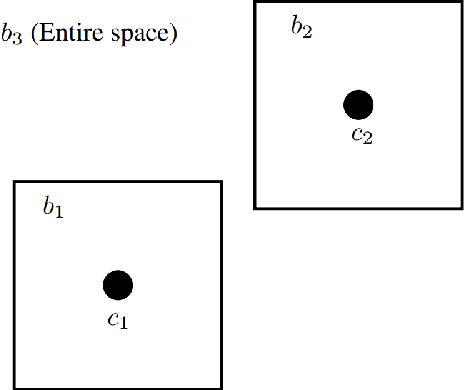
Apr 30, 2020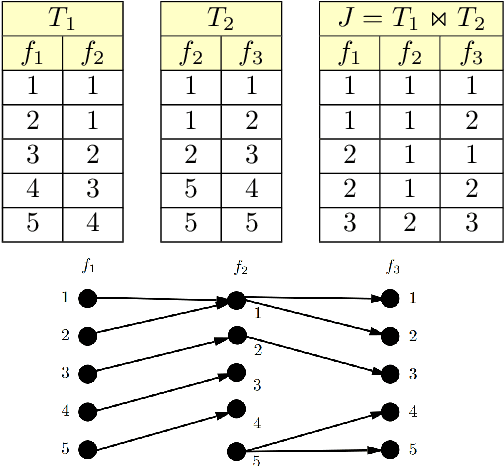
Abstract:We consider the problem of evaluating certain types of functional aggregation queries on relational data subject to additive inequalities. Such aggregation queries, with a smallish number of additive inequalities, arise naturally/commonly in many applications, particularly in learning applications. We give a relatively complete categorization of the computational complexity of such problems. We first show that the problem is NP-hard, even in the case of one additive inequality. Thus we turn to approximating the query. Our main result is an efficient algorithm for approximating, with arbitrarily small relative error, many natural aggregation queries with one additive inequality. We give examples of natural queries that can be efficiently solved using this algorithm. In contrast, we show that the situation with two additive inequalities is quite different, by showing that it is NP-hard to evaluate simple aggregation queries, with two additive inequalities, with any bounded relative error.
On Coresets for Regularized Loss Minimization
May 31, 2019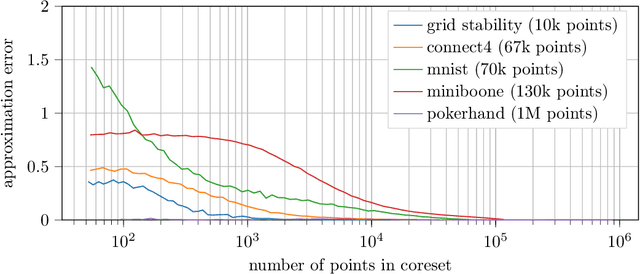

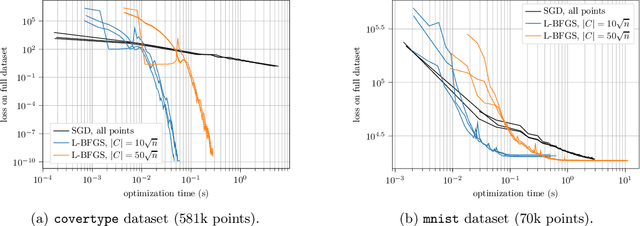
Abstract:We design and mathematically analyze sampling-based algorithms for regularized loss minimization problems that are implementable in popular computational models for large data, in which the access to the data is restricted in some way. Our main result is that if the regularizer's effect does not become negligible as the norm of the hypothesis scales, and as the data scales, then a uniform sample of modest size is with high probability a coreset. In the case that the loss function is either logistic regression or soft-margin support vector machines, and the regularizer is one of the common recommended choices, this result implies that a uniform sample of size $O(d \sqrt{n})$ is with high probability a coreset of $n$ points in $\Re^d$. We contrast this upper bound with two lower bounds. The first lower bound shows that our analysis of uniform sampling is tight; that is, a smaller uniform sample will likely not be a core set. The second lower bound shows that in some sense uniform sampling is close to optimal, as significantly smaller core sets do not generally exist.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge