Incremental Approximate Single-Source Shortest Paths with Predictions

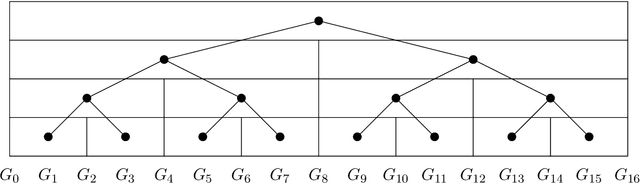
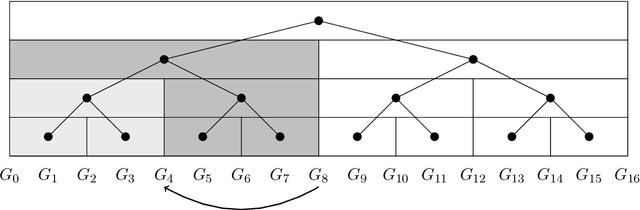
The algorithms-with-predictions framework has been used extensively to develop online algorithms with improved beyond-worst-case competitive ratios. Recently, there is growing interest in leveraging predictions for designing data structures with improved beyond-worst-case running times. In this paper, we study the fundamental data structure problem of maintaining approximate shortest paths in incremental graphs in the algorithms-with-predictions model. Given a sequence $\sigma$ of edges that are inserted one at a time, the goal is to maintain approximate shortest paths from the source to each vertex in the graph at each time step. Before any edges arrive, the data structure is given a prediction of the online edge sequence $\hat{\sigma}$ which is used to ``warm start'' its state. As our main result, we design a learned algorithm that maintains $(1+\epsilon)$-approximate single-source shortest paths, which runs in $\tilde{O}(m \eta \log W/\epsilon)$ time, where $W$ is the weight of the heaviest edge and $\eta$ is the prediction error. We show these techniques immediately extend to the all-pairs shortest-path setting as well. Our algorithms are consistent (performing nearly as fast as the offline algorithm) when predictions are nearly perfect, have a smooth degradation in performance with respect to the prediction error and, in the worst case, match the best offline algorithm up to logarithmic factors. As a building block, we study the offline incremental approximate single-source shortest-paths problem. In this problem, the edge sequence $\sigma$ is known a priori and the goal is to efficiently return the length of the shortest paths in the intermediate graph $G_t$ consisting of the first $t$ edges, for all $t$. Note that the offline incremental problem is defined in the worst-case setting (without predictions) and is of independent interest.

Binary Search with Distributional Predictions

Algorithms with (machine-learned) predictions is a powerful framework for combining traditional worst-case algorithms with modern machine learning. However, the vast majority of work in this space assumes that the prediction itself is non-probabilistic, even if it is generated by some stochastic process (such as a machine learning system). This is a poor fit for modern ML, particularly modern neural networks, which naturally generate a distribution. We initiate the study of algorithms with distributional predictions, where the prediction itself is a distribution. We focus on one of the simplest yet fundamental settings: binary search (or searching a sorted array). This setting has one of the simplest algorithms with a point prediction, but what happens if the prediction is a distribution? We show that this is a richer setting: there are simple distributions where using the classical prediction-based algorithm with any single prediction does poorly. Motivated by this, as our main result, we give an algorithm with query complexity $O(H(p) + \log \eta)$, where $H(p)$ is the entropy of the true distribution $p$ and $\eta$ is the earth mover's distance between $p$ and the predicted distribution $\hat p$. This also yields the first distributionally-robust algorithm for the classical problem of computing an optimal binary search tree given a distribution over target keys. We complement this with a lower bound showing that this query complexity is essentially optimal (up to constants), and experiments validating the practical usefulness of our algorithm.

Best of Many in Both Worlds: Online Resource Allocation with Predictions under Unknown Arrival Model

Online decision-makers today can often obtain predictions on future variables, such as arrivals, demands, inventories, and so on. These predictions can be generated from simple forecasting algorithms for univariate time-series, all the way to state-of-the-art machine learning models that leverage multiple time-series and additional feature information. However, the prediction quality is often unknown to decisions-makers a priori, hence blindly following the predictions can be harmful. In this paper, we address this problem by giving algorithms that take predictions as inputs and perform robustly against the unknown prediction quality. We consider the online resource allocation problem, one of the most generic models in revenue management and online decision-making. In this problem, a decision maker has a limited amount of resources, and requests arrive sequentially. For each request, the decision-maker needs to decide on an action, which generates a certain amount of rewards and consumes a certain amount of resources, without knowing the future requests. The decision-maker's objective is to maximize the total rewards subject to resource constraints. We take the shadow price of each resource as prediction, which can be obtained by predictions on future requests. Prediction quality is naturally defined to be the $\ell_1$ distance between the prediction and the actual shadow price. Our main contribution is an algorithm which takes the prediction of unknown quality as an input, and achieves asymptotically optimal performance under both requests arrival models (stochastic and adversarial) without knowing the prediction quality and the requests arrival model beforehand. We show our algorithm's performance matches the best achievable performance of any algorithm had the arrival models and the accuracy of the predictions been known. We empirically validate our algorithm with experiments.

Online Dynamic Acknowledgement with Learned Predictions

We revisit the online dynamic acknowledgment problem. In the problem, a sequence of requests arrive over time to be acknowledged, and all outstanding requests can be satisfied simultaneously by one acknowledgement. The goal of the problem is to minimize the total request delay plus acknowledgement cost. This elegant model studies the trade-off between acknowledgement cost and waiting experienced by requests. The problem has been well studied and the tight competitive ratios have been determined. For this well-studied problem, we focus on how to effectively use machine-learned predictions to have better performance. We develop algorithms that perform arbitrarily close to the optimum with accurate predictions while concurrently having the guarantees arbitrarily close to what the best online algorithms can offer without access to predictions, thereby achieving simultaneous optimum consistency and robustness. This new result is enabled by our novel prediction error measure. No error measure was defined for the problem prior to our work, and natural measures failed due to the challenge that requests with different arrival times have different effects on the objective. We hope our ideas can be used for other online problems with temporal aspects that have been resisting proper error measures.

Online List Labeling with Predictions

A growing line of work shows how learned predictions can be used to break through worst-case barriers to improve the running time of an algorithm. However, incorporating predictions into data structures with strong theoretical guarantees remains underdeveloped. This paper takes a step in this direction by showing that predictions can be leveraged in the fundamental online list labeling problem. In the problem, n items arrive over time and must be stored in sorted order in an array of size Theta(n). The array slot of an element is its label and the goal is to maintain sorted order while minimizing the total number of elements moved (i.e., relabeled). We design a new list labeling data structure and bound its performance in two models. In the worst-case learning-augmented model, we give guarantees in terms of the error in the predictions. Our data structure provides strong guarantees: it is optimal for any prediction error and guarantees the best-known worst-case bound even when the predictions are entirely erroneous. We also consider a stochastic error model and bound the performance in terms of the expectation and variance of the error. Finally, the theoretical results are demonstrated empirically. In particular, we show that our data structure has strong performance on real temporal data sets where predictions are constructed from elements that arrived in the past, as is typically done in a practical use case.

Learning-Augmented Algorithms for Online Steiner Tree

This paper considers the recently popular beyond-worst-case algorithm analysis model which integrates machine-learned predictions with online algorithm design. We consider the online Steiner tree problem in this model for both directed and undirected graphs. Steiner tree is known to have strong lower bounds in the online setting and any algorithm's worst-case guarantee is far from desirable. This paper considers algorithms that predict which terminal arrives online. The predictions may be incorrect and the algorithms' performance is parameterized by the number of incorrectly predicted terminals. These guarantees ensure that algorithms break through the online lower bounds with good predictions and the competitive ratio gracefully degrades as the prediction error grows. We then observe that the theory is predictive of what will occur empirically. We show on graphs where terminals are drawn from a distribution, the new online algorithms have strong performance even with modestly correct predictions.

Faster Matchings via Learned Duals

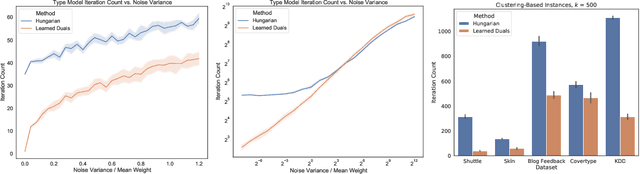
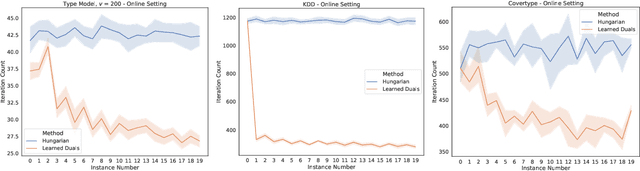
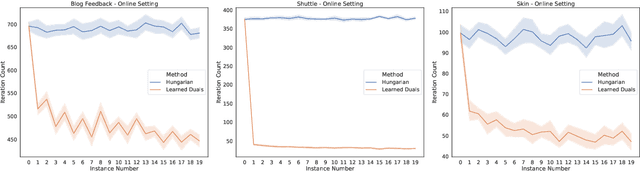
A recent line of research investigates how algorithms can be augmented with machine-learned predictions to overcome worst case lower bounds. This area has revealed interesting algorithmic insights into problems, with particular success in the design of competitive online algorithms. However, the question of improving algorithm running times with predictions has largely been unexplored. We take a first step in this direction by combining the idea of machine-learned predictions with the idea of "warm-starting" primal-dual algorithms. We consider one of the most important primitives in combinatorial optimization: weighted bipartite matching and its generalization to $b$-matching. We identify three key challenges when using learned dual variables in a primal-dual algorithm. First, predicted duals may be infeasible, so we give an algorithm that efficiently maps predicted infeasible duals to nearby feasible solutions. Second, once the duals are feasible, they may not be optimal, so we show that they can be used to quickly find an optimal solution. Finally, such predictions are useful only if they can be learned, so we show that the problem of learning duals for matching has low sample complexity. We validate our theoretical findings through experiments on both real and synthetic data. As a result we give a rigorous, practical, and empirically effective method to compute bipartite matchings.

Learnable and Instance-Robust Predictions for Online Matching, Flows and Load Balancing

This paper proposes a new model for augmenting algorithms with useful predictions that go beyond worst-case bounds on the algorithm performance. By refining existing models, our model ensures predictions are formally learnable and instance robust. Learnability guarantees that predictions can be efficiently constructed from past data. Instance robustness formally ensures a prediction is robust to modest changes in the problem input. Further, the robustness model ensures two different predictions can be objectively compared, addressing a shortcoming in prior models. This paper establishes the existence of predictions which satisfy these properties. The paper considers online algorithms with predictions for a network flow allocation problem and the restricted assignment makespan minimization problem. For both problems, three key properties are established: existence of useful predictions that give near optimal solutions, robustness of these predictions to errors that smoothly degrade as the underlying problem instance changes, and we prove high quality predictions can be learned from a small sample of prior instances.

An Objective for Hierarchical Clustering in Euclidean Space and its Connection to Bisecting K-means

This paper explores hierarchical clustering in the case where pairs of points have dissimilarity scores (e.g. distances) as a part of the input. The recently introduced objective for points with dissimilarity scores results in every tree being a 1/2 approximation if the distances form a metric. This shows the objective does not make a significant distinction between a good and poor hierarchical clustering in metric spaces. Motivated by this, the paper develops a new global objective for hierarchical clustering in Euclidean space. The objective captures the criterion that has motivated the use of divisive clustering algorithms: that when a split happens, points in the same cluster should be more similar than points in different clusters. Moreover, this objective gives reasonable results on ground-truth inputs for hierarchical clustering. The paper builds a theoretical connection between this objective and the bisecting k-means algorithm. This paper proves that the optimal 2-means solution results in a constant approximation for the objective. This is the first paper to show the bisecting k-means algorithm optimizes a natural global objective over the entire tree.

Relational Algorithms for k-means Clustering

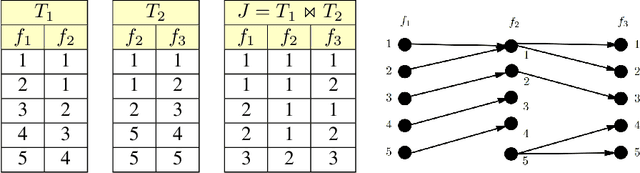
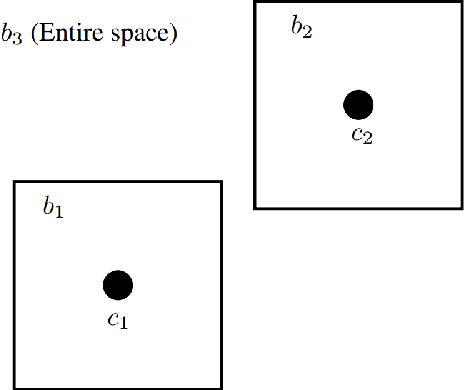
The majority of learning tasks faced by data scientists involve relational data, yet most standard algorithms for standard learning problems are not designed to accept relational data as input. The standard practice to address this issue is to join the relational data to create the type of geometric input that standard learning algorithms expect. Unfortunately, this standard practice has exponential worst-case time and space complexity. This leads us to consider what we call the Relational Learning Question: ``Which standard learning algorithms can be efficiently implemented on relational data, and for those that can not, is there an alternative algorithm that can be efficiently implemented on relational data and that has similar performance guarantees to the standard algorithm?'' In this paper, we address the relational learning question for two well-known algorithms for the standard $k$-means clustering problem. We first show that the $k$-means++ algorithm can be efficiently implemented on relational data. In contrast, we show that the adaptive $k$-means algorithm likely can not be efficiently implemented on relational data, as this would imply $P = \#P$. However, we show that a slight variation of this adaptive $k$-means algorithm can be efficiently implemented on relational data, and that this alternative algorithm has the same performance guarantee as the original algorithm, that is that it outputs an $O(1)$-approximate sketch.