Binary Search with Distributional Predictions

Algorithms with (machine-learned) predictions is a powerful framework for combining traditional worst-case algorithms with modern machine learning. However, the vast majority of work in this space assumes that the prediction itself is non-probabilistic, even if it is generated by some stochastic process (such as a machine learning system). This is a poor fit for modern ML, particularly modern neural networks, which naturally generate a distribution. We initiate the study of algorithms with distributional predictions, where the prediction itself is a distribution. We focus on one of the simplest yet fundamental settings: binary search (or searching a sorted array). This setting has one of the simplest algorithms with a point prediction, but what happens if the prediction is a distribution? We show that this is a richer setting: there are simple distributions where using the classical prediction-based algorithm with any single prediction does poorly. Motivated by this, as our main result, we give an algorithm with query complexity $O(H(p) + \log \eta)$, where $H(p)$ is the entropy of the true distribution $p$ and $\eta$ is the earth mover's distance between $p$ and the predicted distribution $\hat p$. This also yields the first distributionally-robust algorithm for the classical problem of computing an optimal binary search tree given a distribution over target keys. We complement this with a lower bound showing that this query complexity is essentially optimal (up to constants), and experiments validating the practical usefulness of our algorithm.

From Stream to Pool: Dynamic Pricing Beyond i.i.d. Arrivals

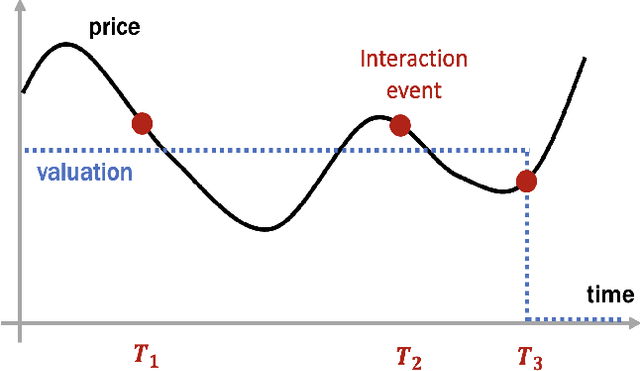
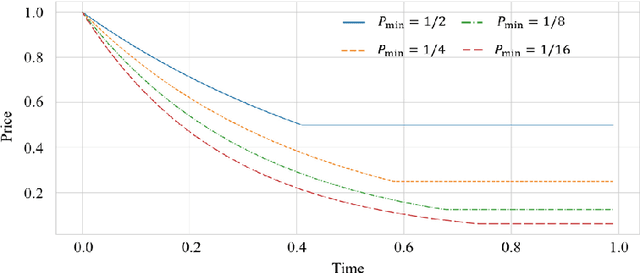
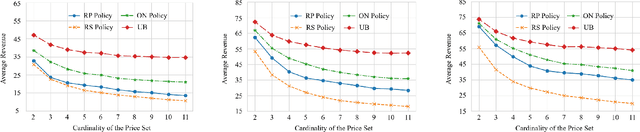
The dynamic pricing problem has been extensively studied under the \textbf{stream} model: A stream of customers arrives sequentially, each with an independently and identically distributed valuation. However, this formulation is not entirely reflective of the real world. In many scenarios, high-valuation customers tend to make purchases earlier and leave the market, leading to a \emph{shift} in the valuation distribution. Thus motivated, we consider a model where a \textbf{pool} of $n$ non-strategic unit-demand customers interact repeatedly with the seller. Each customer monitors the price intermittently according to an independent Poisson process and makes a purchase if the observed price is lower than her \emph{private} valuation, whereupon she leaves the market permanently. We present a minimax \emph{optimal} algorithm that efficiently computes a non-adaptive policy which guarantees a $1/k$ fraction of the optimal revenue, given any set of $k$ prices. Moreover, we present an adaptive \emph{learn-then-earn} policy based on a novel \emph{debiasing} approach, and prove an $\tilde O(kn^{3/4})$ regret bound. We further improve the bound to $\tilde O(k^{3/4} n^{3/4})$ using martingale concentration inequalities.

Faster Matchings via Learned Duals

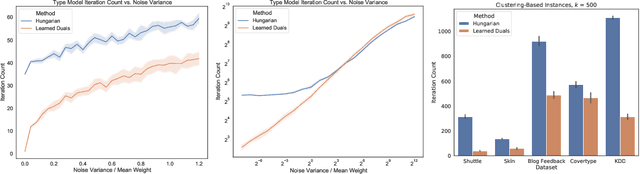
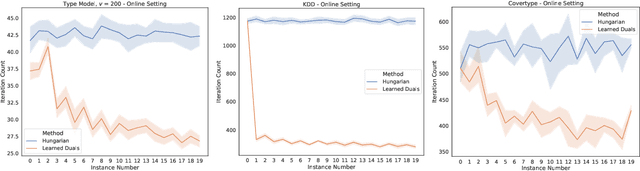
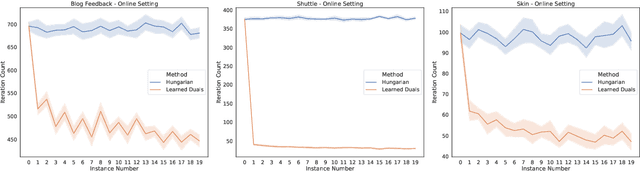
A recent line of research investigates how algorithms can be augmented with machine-learned predictions to overcome worst case lower bounds. This area has revealed interesting algorithmic insights into problems, with particular success in the design of competitive online algorithms. However, the question of improving algorithm running times with predictions has largely been unexplored. We take a first step in this direction by combining the idea of machine-learned predictions with the idea of "warm-starting" primal-dual algorithms. We consider one of the most important primitives in combinatorial optimization: weighted bipartite matching and its generalization to $b$-matching. We identify three key challenges when using learned dual variables in a primal-dual algorithm. First, predicted duals may be infeasible, so we give an algorithm that efficiently maps predicted infeasible duals to nearby feasible solutions. Second, once the duals are feasible, they may not be optimal, so we show that they can be used to quickly find an optimal solution. Finally, such predictions are useful only if they can be learned, so we show that the problem of learning duals for matching has low sample complexity. We validate our theoretical findings through experiments on both real and synthetic data. As a result we give a rigorous, practical, and empirically effective method to compute bipartite matchings.

Learnable and Instance-Robust Predictions for Online Matching, Flows and Load Balancing

This paper proposes a new model for augmenting algorithms with useful predictions that go beyond worst-case bounds on the algorithm performance. By refining existing models, our model ensures predictions are formally learnable and instance robust. Learnability guarantees that predictions can be efficiently constructed from past data. Instance robustness formally ensures a prediction is robust to modest changes in the problem input. Further, the robustness model ensures two different predictions can be objectively compared, addressing a shortcoming in prior models. This paper establishes the existence of predictions which satisfy these properties. The paper considers online algorithms with predictions for a network flow allocation problem and the restricted assignment makespan minimization problem. For both problems, three key properties are established: existence of useful predictions that give near optimal solutions, robustness of these predictions to errors that smoothly degrade as the underlying problem instance changes, and we prove high quality predictions can be learned from a small sample of prior instances.