Titing Cui
From Stream to Pool: Dynamic Pricing Beyond i.i.d. Arrivals
Oct 30, 2023
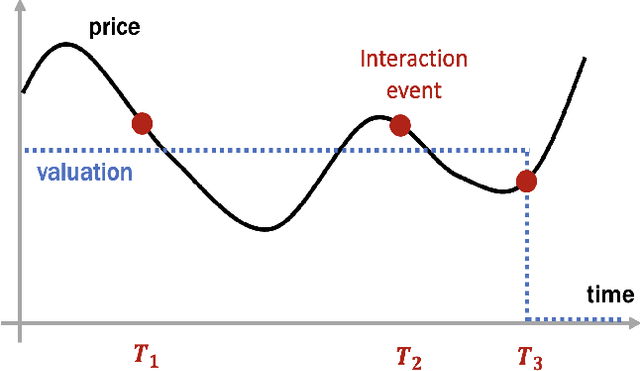
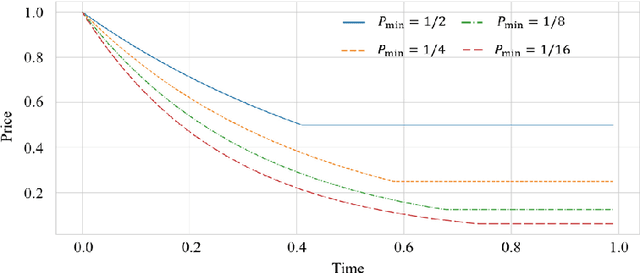
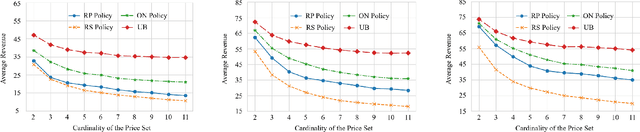
Abstract:The dynamic pricing problem has been extensively studied under the \textbf{stream} model: A stream of customers arrives sequentially, each with an independently and identically distributed valuation. However, this formulation is not entirely reflective of the real world. In many scenarios, high-valuation customers tend to make purchases earlier and leave the market, leading to a \emph{shift} in the valuation distribution. Thus motivated, we consider a model where a \textbf{pool} of $n$ non-strategic unit-demand customers interact repeatedly with the seller. Each customer monitors the price intermittently according to an independent Poisson process and makes a purchase if the observed price is lower than her \emph{private} valuation, whereupon she leaves the market permanently. We present a minimax \emph{optimal} algorithm that efficiently computes a non-adaptive policy which guarantees a $1/k$ fraction of the optimal revenue, given any set of $k$ prices. Moreover, we present an adaptive \emph{learn-then-earn} policy based on a novel \emph{debiasing} approach, and prove an $\tilde O(kn^{3/4})$ regret bound. We further improve the bound to $\tilde O(k^{3/4} n^{3/4})$ using martingale concentration inequalities.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge