Modern, Efficient, and Differentiable Transport Equation Models using JAX: Applications to Population Balance Equations

Population balance equation (PBE) models have potential to automate many engineering processes with far-reaching implications. In the pharmaceutical sector, crystallization model-based design can contribute to shortening excessive drug development timelines. Even so, two major barriers, typical of most transport equations, not just PBEs, have limited this potential. Notably, the time taken to compute a solution to these models with representative accuracy is frequently limiting. Likewise, the model construction process is often tedious and wastes valuable time, owing to the reliance on human expertise to guess constituent models from empirical data. Hybrid models promise to overcome both barriers through tight integration of neural networks with physical PBE models. Towards eliminating experimental guesswork, hybrid models facilitate determining physical relationships from data, also known as 'discovering physics'. Here, we aim to prepare for planned Scientific Machine Learning (SciML) integration through a contemporary implementation of an existing PBE algorithm, one with computational efficiency and differentiability at the forefront. To accomplish this, we utilized JAX, a cutting-edge library for accelerated computing. We showcase the speed benefits of this modern take on PBE modelling by benchmarking our solver to others we prepared using older, more widespread software. Primarily among these software tools is the ubiquitous NumPy, where we show JAX achieves up to 300x relative acceleration in PBE simulations. Our solver is also fully differentiable, which we demonstrate is the only feasible option for integrating learnable data-driven models at scale. We show that differentiability can be 40x faster for optimizing larger models than conventional approaches, which represents the key to neural network integration for physics discovery in later work.

Finite Basis Physics-Informed Neural Networks (FBPINNs): a scalable domain decomposition approach for solving differential equations

Recently, physics-informed neural networks (PINNs) have offered a powerful new paradigm for solving problems relating to differential equations. Compared to classical numerical methods PINNs have several advantages, for example their ability to provide mesh-free solutions of differential equations and their ability to carry out forward and inverse modelling within the same optimisation problem. Whilst promising, a key limitation to date is that PINNs have struggled to accurately and efficiently solve problems with large domains and/or multi-scale solutions, which is crucial for their real-world application. Multiple significant and related factors contribute to this issue, including the increasing complexity of the underlying PINN optimisation problem as the problem size grows and the spectral bias of neural networks. In this work we propose a new, scalable approach for solving large problems relating to differential equations called Finite Basis PINNs (FBPINNs). FBPINNs are inspired by classical finite element methods, where the solution of the differential equation is expressed as the sum of a finite set of basis functions with compact support. In FBPINNs neural networks are used to learn these basis functions, which are defined over small, overlapping subdomains. FBINNs are designed to address the spectral bias of neural networks by using separate input normalisation over each subdomain, and reduce the complexity of the underlying optimisation problem by using many smaller neural networks in a parallel divide-and-conquer approach. Our numerical experiments show that FBPINNs are effective in solving both small and larger, multi-scale problems, outperforming standard PINNs in both accuracy and computational resources required, potentially paving the way to the application of PINNs on large, real-world problems.

Rk-means: Fast Clustering for Relational Data

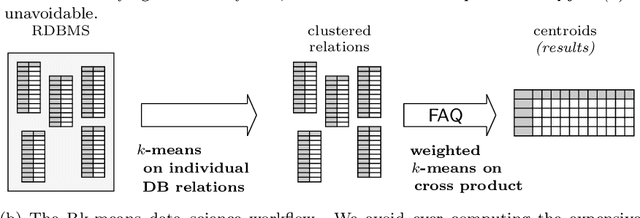
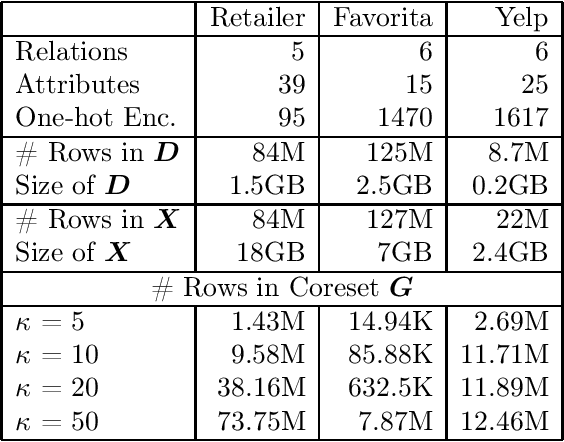
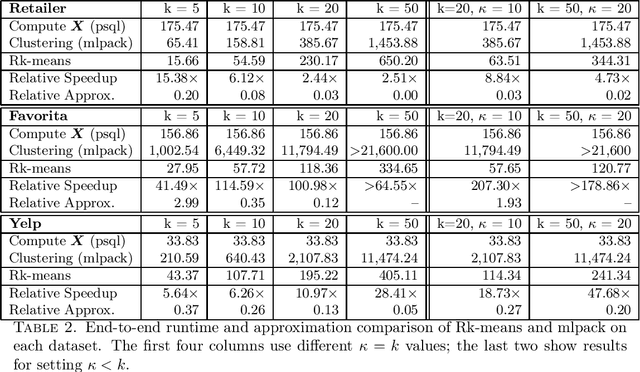
Conventional machine learning algorithms cannot be applied until a data matrix is available to process. When the data matrix needs to be obtained from a relational database via a feature extraction query, the computation cost can be prohibitive, as the data matrix may be (much) larger than the total input relation size. This paper introduces Rk-means, or relational k -means algorithm, for clustering relational data tuples without having to access the full data matrix. As such, we avoid having to run the expensive feature extraction query and storing its output. Our algorithm leverages the underlying structures in relational data. It involves construction of a small {\it grid coreset} of the data matrix for subsequent cluster construction. This gives a constant approximation for the k -means objective, while having asymptotic runtime improvements over standard approaches of first running the database query and then clustering. Empirical results show orders-of-magnitude speedup, and Rk-means can run faster on the database than even just computing the data matrix.

On Coresets for Regularized Loss Minimization

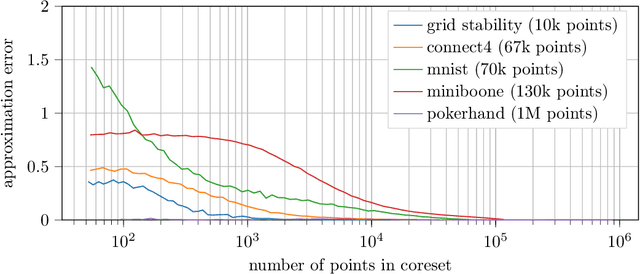
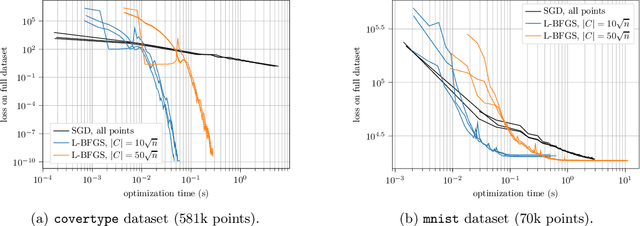
We design and mathematically analyze sampling-based algorithms for regularized loss minimization problems that are implementable in popular computational models for large data, in which the access to the data is restricted in some way. Our main result is that if the regularizer's effect does not become negligible as the norm of the hypothesis scales, and as the data scales, then a uniform sample of modest size is with high probability a coreset. In the case that the loss function is either logistic regression or soft-margin support vector machines, and the regularizer is one of the common recommended choices, this result implies that a uniform sample of size $O(d \sqrt{n})$ is with high probability a coreset of $n$ points in $\Re^d$. We contrast this upper bound with two lower bounds. The first lower bound shows that our analysis of uniform sampling is tight; that is, a smaller uniform sample will likely not be a core set. The second lower bound shows that in some sense uniform sampling is close to optimal, as significantly smaller core sets do not generally exist.