Maximilian Schleich
Computing Rule-Based Explanations by Leveraging Counterfactuals
Oct 31, 2022
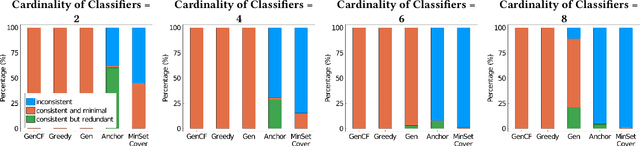
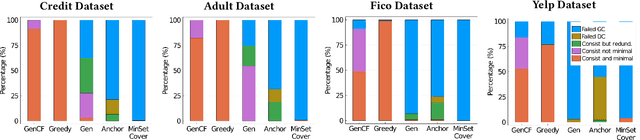

Abstract:Sophisticated machine models are increasingly used for high-stakes decisions in everyday life. There is an urgent need to develop effective explanation techniques for such automated decisions. Rule-Based Explanations have been proposed for high-stake decisions like loan applications, because they increase the users' trust in the decision. However, rule-based explanations are very inefficient to compute, and existing systems sacrifice their quality in order to achieve reasonable performance. We propose a novel approach to compute rule-based explanations, by using a different type of explanation, Counterfactual Explanations, for which several efficient systems have already been developed. We prove a Duality Theorem, showing that rule-based and counterfactual-based explanations are dual to each other, then use this observation to develop an efficient algorithm for computing rule-based explanations, which uses the counterfactual-based explanation as an oracle. We conduct extensive experiments showing that our system computes rule-based explanations of higher quality, and with the same or better performance, than two previous systems, MinSetCover and Anchor.
GeCo: Quality Counterfactual Explanations in Real Time
Jan 05, 2021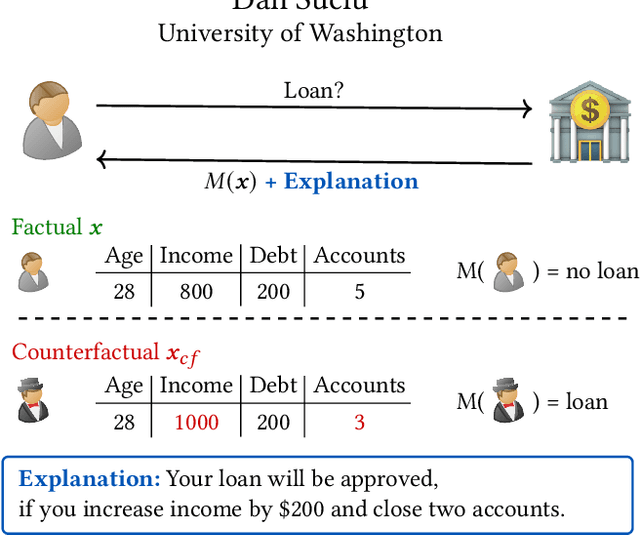
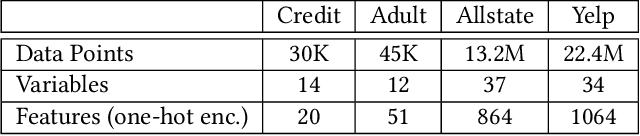

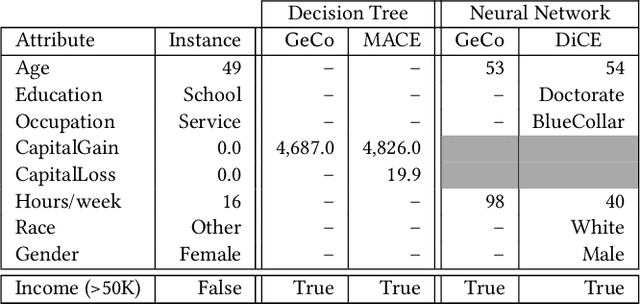
Abstract:Machine learning is increasingly applied in high-stakes decision making that directly affect people's lives, and this leads to an increased demand for systems to explain their decisions. Explanations often take the form of counterfactuals, which consists of conveying to the end user what she/he needs to change in order to improve the outcome. Computing counterfactual explanations is challenging, because of the inherent tension between a rich semantics of the domain, and the need for real time response. In this paper we present GeCo, the first system that can compute plausible and feasible counterfactual explanations in real time. At its core, GeCo relies on a genetic algorithm, which is customized to favor searching counterfactual explanations with the smallest number of changes. To achieve real-time performance, we introduce two novel optimizations: $\Delta$-representation of candidate counterfactuals, and partial evaluation of the classifier. We compare empirically GeCo against four other systems described in the literature, and show that it is the only system that can achieve both high quality explanations and real time answers.
On the Tractability of SHAP Explanations
Sep 18, 2020Abstract:SHAP explanations are a popular feature-attribution mechanism for explainable AI. They use game-theoretic notions to measure the influence of individual features on the prediction of a machine learning model. Despite a lot of recent interest from both academia and industry, it is not known whether SHAP explanations of common machine learning models can be computed efficiently. In this paper, we establish the complexity of computing the SHAP explanation in three important settings. First, we consider fully-factorized data distributions, and show that the complexity of computing the SHAP explanation is the same as the complexity of computing the expected value of the model. This fully-factorized setting is often used to simplify the SHAP computation, yet our results show that the computation can be intractable for commonly used models such as logistic regression. Going beyond fully-factorized distributions, we show that computing SHAP explanations is already intractable for a very simple setting: computing SHAP explanations of trivial classifiers over naive Bayes distributions. Finally, we show that even computing SHAP over the empirical distribution is #P-hard.
Causality-based Explanation of Classification Outcomes
Mar 15, 2020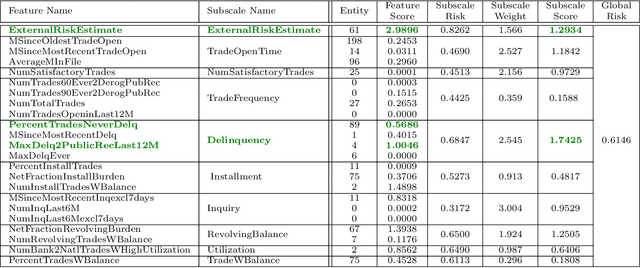

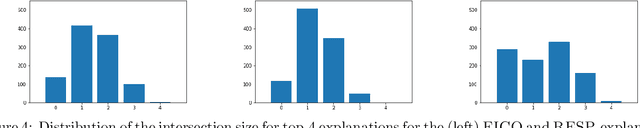
Abstract:We propose a simple definition of an explanation for the outcome of a classifier based on concepts from causality. We compare it with previously proposed notions of explanation, and study their complexity. We conduct an experimental evaluation with two real datasets from the financial domain.
Multi-layer Optimizations for End-to-End Data Analytics
Jan 10, 2020
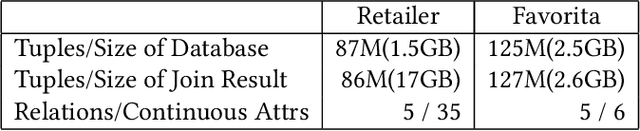
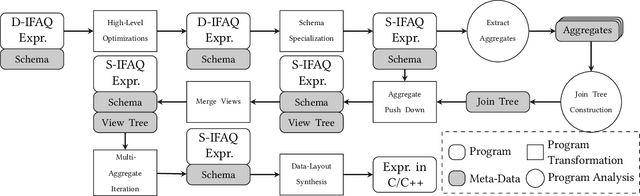

Abstract:We consider the problem of training machine learning models over multi-relational data. The mainstream approach is to first construct the training dataset using a feature extraction query over input database and then use a statistical software package of choice to train the model. In this paper we introduce Iterative Functional Aggregate Queries (IFAQ), a framework that realizes an alternative approach. IFAQ treats the feature extraction query and the learning task as one program given in the IFAQ's domain-specific language, which captures a subset of Python commonly used in Jupyter notebooks for rapid prototyping of machine learning applications. The program is subject to several layers of IFAQ optimizations, such as algebraic transformations, loop transformations, schema specialization, data layout optimizations, and finally compilation into efficient low-level C++ code specialized for the given workload and data. We show that a Scala implementation of IFAQ can outperform mlpack, Scikit, and TensorFlow by several orders of magnitude for linear regression and regression tree models over several relational datasets.
Rk-means: Fast Clustering for Relational Data
Oct 11, 2019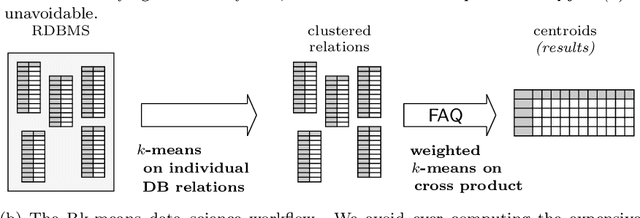
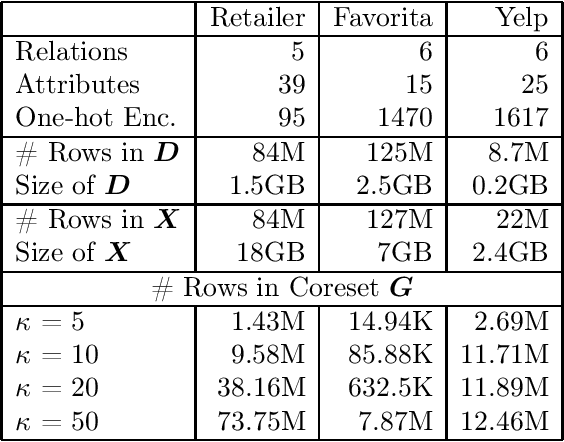
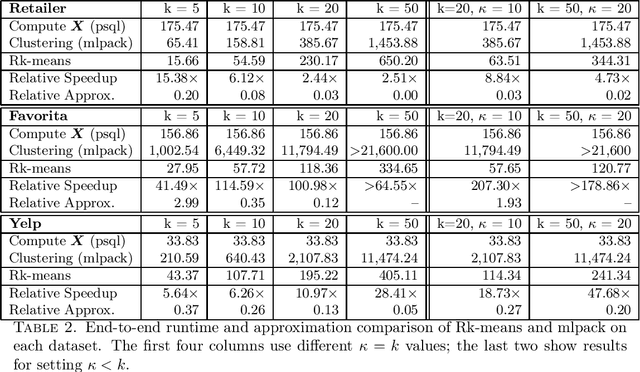
Abstract:Conventional machine learning algorithms cannot be applied until a data matrix is available to process. When the data matrix needs to be obtained from a relational database via a feature extraction query, the computation cost can be prohibitive, as the data matrix may be (much) larger than the total input relation size. This paper introduces Rk-means, or relational k -means algorithm, for clustering relational data tuples without having to access the full data matrix. As such, we avoid having to run the expensive feature extraction query and storing its output. Our algorithm leverages the underlying structures in relational data. It involves construction of a small {\it grid coreset} of the data matrix for subsequent cluster construction. This gives a constant approximation for the k -means objective, while having asymptotic runtime improvements over standard approaches of first running the database query and then clustering. Empirical results show orders-of-magnitude speedup, and Rk-means can run faster on the database than even just computing the data matrix.
On Functional Aggregate Queries with Additive Inequalities
Dec 22, 2018
Abstract:Motivated by fundamental applications in databases and relational machine learning, we formulate and study the problem of answering Functional Aggregate Queries (FAQ) in which some of the input factors are defined by a collection of Additive Inequalities between variables. We refer to these queries as FAQ-AI for short. To answer FAQ-AI in the Boolean semiring, we define "relaxed" tree decompositions and "relaxed" submodular and fractional hypertree width parameters. We show that an extension of the InsideOut algorithm using Chazelle's geometric data structure for solving the semigroup range search problem can answer Boolean FAQ-AI in time given by these new width parameters. This new algorithm achieves lower complexity than known solutions for FAQ-AI. It also recovers some known results in database query answering. Our second contribution is a relaxation of the set of polymatroids that gives rise to the counting version of the submodular width, denoted by "#subw". This new width is sandwiched between the submodular and the fractional hypertree widths. Any FAQ and FAQ-AI over one semiring can be answered in time proportional to #subw and respectively to the relaxed version of #subw. We present three applications of our FAQ-AI framework to relational machine learning: k-means clustering, training linear support vector machines, and training models using non-polynomial loss. These optimization problems can be solved over a database asymptotically faster than computing the join of the database relations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge