Compressing Structured Tensor Algebra

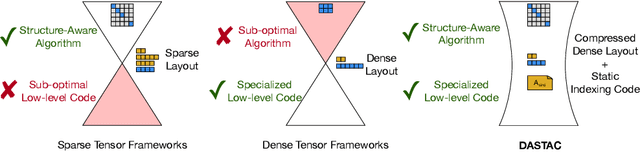
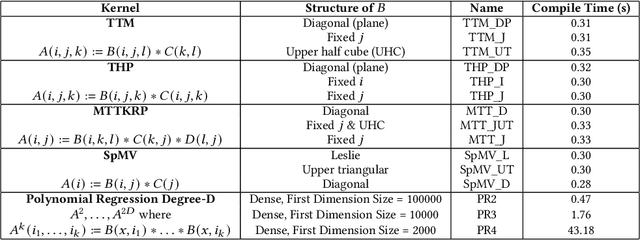
Tensor algebra is a crucial component for data-intensive workloads such as machine learning and scientific computing. As the complexity of data grows, scientists often encounter a dilemma between the highly specialized dense tensor algebra and efficient structure-aware algorithms provided by sparse tensor algebra. In this paper, we introduce DASTAC, a framework to propagate the tensors's captured high-level structure down to low-level code generation by incorporating techniques such as automatic data layout compression, polyhedral analysis, and affine code generation. Our methodology reduces memory footprint by automatically detecting the best data layout, heavily benefits from polyhedral optimizations, leverages further optimizations, and enables parallelization through MLIR. Through extensive experimentation, we show that DASTAC achieves 1 to 2 orders of magnitude speedup over TACO, a state-of-the-art sparse tensor compiler, and StructTensor, a state-of-the-art structured tensor algebra compiler, with a significantly lower memory footprint.

$ abla$SD: Differentiable Programming for Sparse Tensors

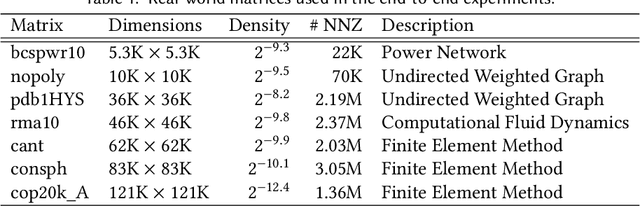
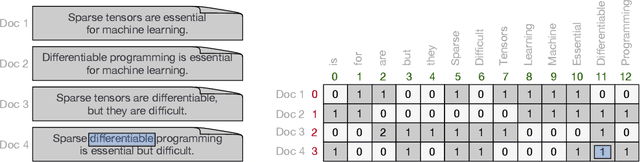
Sparse tensors are prevalent in many data-intensive applications, yet existing differentiable programming frameworks are tailored towards dense tensors. This presents a significant challenge for efficiently computing gradients through sparse tensor operations, as their irregular sparsity patterns can result in substantial memory and computational overheads. In this work, we introduce a novel framework that enables the efficient and automatic differentiation of sparse tensors, addressing this fundamental issue. Our experiments demonstrate the effectiveness of the proposed framework in terms of performance and scalability, outperforming state-of-the-art frameworks across a range of synthetic and real-world datasets. Our approach offers a promising direction for enabling efficient and scalable differentiable programming with sparse tensors, which has significant implications for numerous applications in machine learning, natural language processing, and scientific computing.

Efficient and Sound Differentiable Programming in a Functional Array-Processing Language

Automatic differentiation (AD) is a technique for computing the derivative of a function represented by a program. This technique is considered as the de-facto standard for computing the differentiation in many machine learning and optimisation software tools. Despite the practicality of this technique, the performance of the differentiated programs, especially for functional languages and in the presence of vectors, is suboptimal. We present an AD system for a higher-order functional array-processing language. The core functional language underlying this system simultaneously supports both source-to-source forward-mode AD and global optimisations such as loop transformations. In combination, gradient computation with forward-mode AD can be as efficient as reverse mode, and the Jacobian matrices required for numerical algorithms such as Gauss-Newton and Levenberg-Marquardt can be efficiently computed.

Fine-Tuning Data Structures for Analytical Query Processing

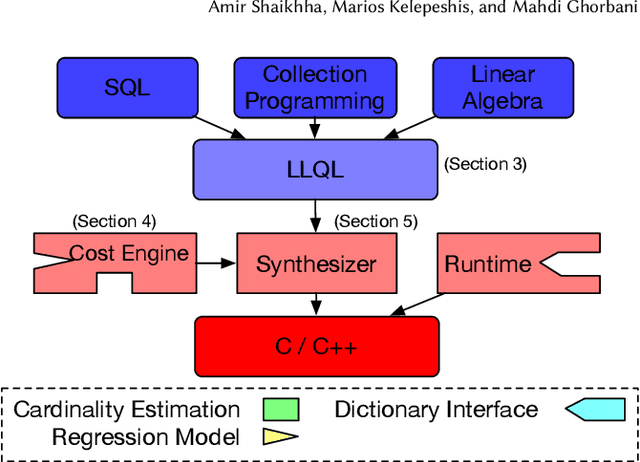
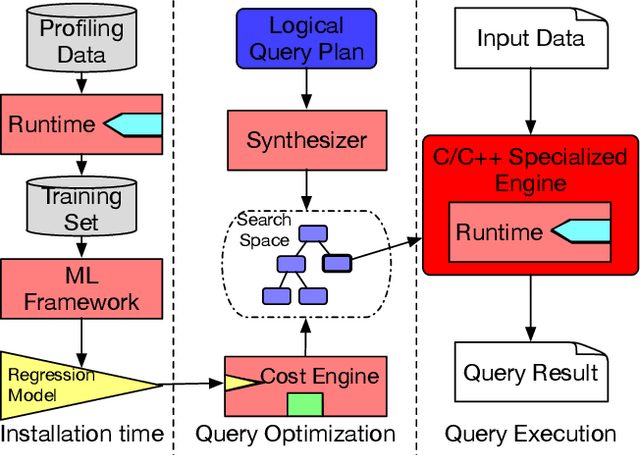
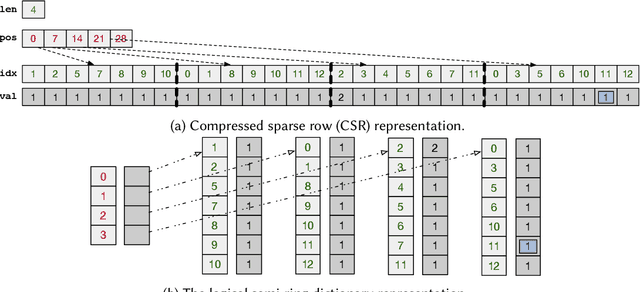
We introduce a framework for automatically choosing data structures to support efficient computation of analytical workloads. Our contributions are twofold. First, we introduce a novel low-level intermediate language that can express the algorithms behind various query processing paradigms such as classical joins, groupjoin, and in-database machine learning engines. This language is designed around the notion of dictionaries, and allows for a more fine-grained choice of its low-level implementation. Second, the cost model for alternative implementations is automatically inferred by combining machine learning and program reasoning. The dictionary cost model is learned using a regression model trained over the profiling dataset of dictionary operations on a given hardware architecture. The program cost model is inferred using static program analysis. Our experimental results show the effectiveness of the trained cost model on micro benchmarks. Furthermore, we show that the performance of the code generated by our framework either outperforms or is on par with the state-of-the-art analytical query engines and a recent in-database machine learning framework.

Functional Collection Programming with Semi-Ring Dictionaries

This paper introduces semi-ring dictionaries, a powerful class of compositional and purely functional collections that subsume other collection types such as sets, multisets, arrays, vectors, and matrices. We develop SDQL, a statically typed language centered around semi-ring dictionaries, that can encode expressions in relational algebra with aggregations, functional collections, and linear algebra. Furthermore, thanks to the semi-ring algebraic structures behind these dictionaries, SDQL unifies a wide range of optimizations commonly used in databases and linear algebra. As a result, SDQL enables efficient processing of hybrid database and linear algebra workloads, by putting together optimizations that are otherwise confined to either database systems or linear algebra frameworks. Through experimental results, we show that a handful of relational and linear algebra workloads can take advantage of the SDQL language and optimizations. Overall, we observe that SDQL achieves competitive performance to Typer and Tectorwise, which are state-of-the-art in-memory systems for (flat, not nested) relational data, and achieves an average 2x speedup over SciPy for linear algebra workloads. Finally, for hybrid workloads involving linear algebra processing over nested biomedical data, SDQL can give up to one order of magnitude speedup over Trance, a state-of-the-art nested relational engine.

BayesCard: Revitilizing Bayesian Frameworks for Cardinality Estimation

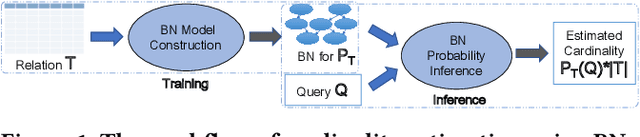
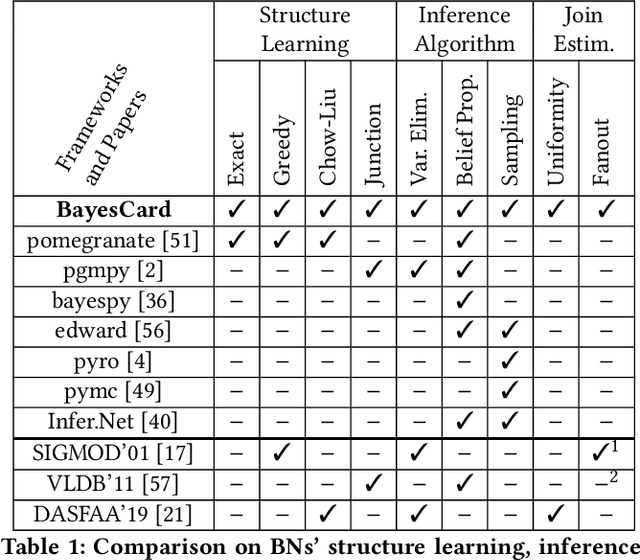
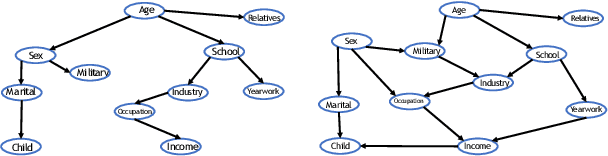
Cardinality estimation (CardEst) is an essential component in query optimizers and a fundamental problem in DBMS. A desired CardEst method should attain good algorithm performance, be stable to varied data settings, and be friendly to system deployment. However, no existing CardEst method can fulfill the three criteria at the same time. Traditional methods often have significant algorithm drawbacks such as large estimation errors. Recently proposed deep learning based methods largely improve the estimation accuracy but their performance can be greatly affected by data and often difficult for system deployment. In this paper, we revitalize the Bayesian networks (BN) for CardEst by incorporating the techniques of probabilistic programming languages. We present BayesCard, the first framework that inherits the advantages of BNs, i.e., high estimation accuracy and interpretability, while overcomes their drawbacks, i.e. low structure learning and inference efficiency. This makes BayesCard a perfect candidate for commercial DBMS deployment. Our experimental results on several single-table and multi-table benchmarks indicate BayesCard's superiority over existing state-of-the-art CardEst methods: BayesCard achieves comparable or better accuracy, 1-2 orders of magnitude faster inference time, 1-3 orders faster training time, 1-3 orders smaller model size, and 1-2 orders faster updates. Meanwhile, BayesCard keeps stable performance when varying data with different settings. We also deploy BayesCard into PostgreSQL. On the IMDB benchmark workload, it improves the end-to-end query time by 13.3%, which is very close to the optimal result of 14.2% using an oracle of true cardinality.

Multi-layer Optimizations for End-to-End Data Analytics

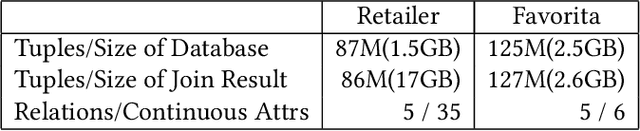
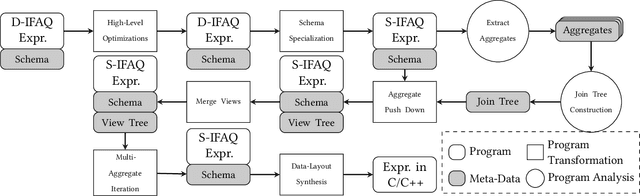
We consider the problem of training machine learning models over multi-relational data. The mainstream approach is to first construct the training dataset using a feature extraction query over input database and then use a statistical software package of choice to train the model. In this paper we introduce Iterative Functional Aggregate Queries (IFAQ), a framework that realizes an alternative approach. IFAQ treats the feature extraction query and the learning task as one program given in the IFAQ's domain-specific language, which captures a subset of Python commonly used in Jupyter notebooks for rapid prototyping of machine learning applications. The program is subject to several layers of IFAQ optimizations, such as algebraic transformations, loop transformations, schema specialization, data layout optimizations, and finally compilation into efficient low-level C++ code specialized for the given workload and data. We show that a Scala implementation of IFAQ can outperform mlpack, Scikit, and TensorFlow by several orders of magnitude for linear regression and regression tree models over several relational datasets.

Efficient Differentiable Programming in a Functional Array-Processing Language

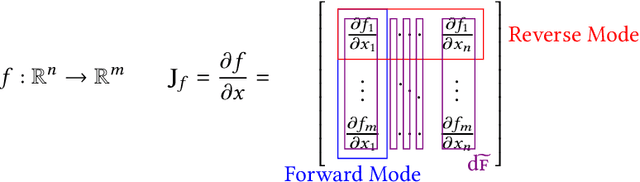
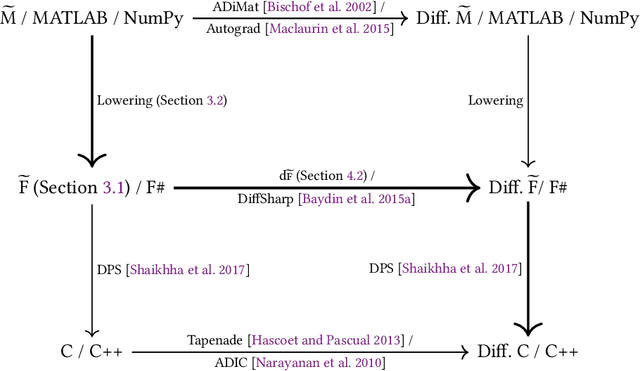
We present a system for the automatic differentiation of a higher-order functional array-processing language. The core functional language underlying this system simultaneously supports both source-to-source automatic differentiation and global optimizations such as loop transformations. Thanks to this feature, we demonstrate how for some real-world machine learning and computer vision benchmarks, the system outperforms the state-of-the-art automatic differentiation tools.