A Relational Gradient Descent Algorithm For Support Vector Machine Training

We consider gradient descent like algorithms for Support Vector Machine (SVM) training when the data is in relational form. The gradient of the SVM objective can not be efficiently computed by known techniques as it suffers from the ``subtraction problem''. We first show that the subtraction problem can not be surmounted by showing that computing any constant approximation of the gradient of the SVM objective function is $\#P$-hard, even for acyclic joins. We, however, circumvent the subtraction problem by restricting our attention to stable instances, which intuitively are instances where a nearly optimal solution remains nearly optimal if the points are perturbed slightly. We give an efficient algorithm that computes a ``pseudo-gradient'' that guarantees convergence for stable instances at a rate comparable to that achieved by using the actual gradient. We believe that our results suggest that this sort of stability the analysis would likely yield useful insight in the context of designing algorithms on relational data for other learning problems in which the subtraction problem arises.

Approximate Aggregate Queries Under Additive Inequalities

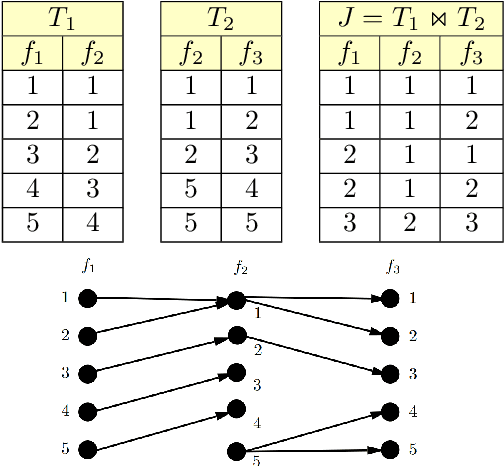
We consider the problem of evaluating certain types of functional aggregation queries on relational data subject to additive inequalities. Such aggregation queries, with a smallish number of additive inequalities, arise naturally/commonly in many applications, particularly in learning applications. We give a relatively complete categorization of the computational complexity of such problems. We first show that the problem is NP-hard, even in the case of one additive inequality. Thus we turn to approximating the query. Our main result is an efficient algorithm for approximating, with arbitrarily small relative error, many natural aggregation queries with one additive inequality. We give examples of natural queries that can be efficiently solved using this algorithm. In contrast, we show that the situation with two additive inequalities is quite different, by showing that it is NP-hard to evaluate simple aggregation queries, with two additive inequalities, with any bounded relative error.