Aditya Petety
Parsimonious Learning-Augmented Caching
Feb 09, 2022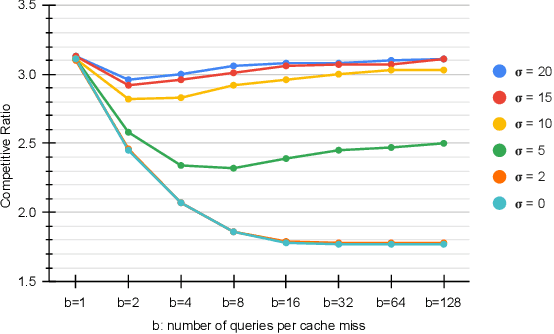
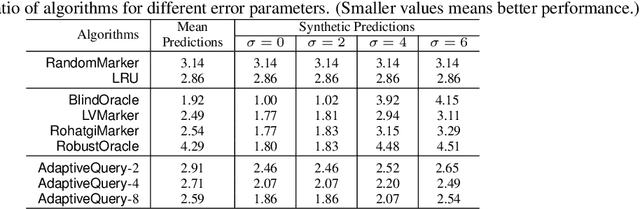
Abstract:Learning-augmented algorithms -- in which, traditional algorithms are augmented with machine-learned predictions -- have emerged as a framework to go beyond worst-case analysis. The overarching goal is to design algorithms that perform near-optimally when the predictions are accurate yet retain certain worst-case guarantees irrespective of the accuracy of the predictions. This framework has been successfully applied to online problems such as caching where the predictions can be used to alleviate uncertainties. In this paper we introduce and study the setting in which the learning-augmented algorithm can utilize the predictions parsimoniously. We consider the caching problem -- which has been extensively studied in the learning-augmented setting -- and show that one can achieve quantitatively similar results but only using a sublinear number of predictions.
Attribute noise robust binary classification
Nov 18, 2019



Abstract:We consider the problem of learning linear classifiers when both features and labels are binary. In addition, the features are noisy, i.e., they could be flipped with an unknown probability. In Sy-De attribute noise model, where all features could be noisy together with same probability, we show that $0$-$1$ loss ($l_{0-1}$) need not be robust but a popular surrogate, squared loss ($l_{sq}$) is. In Asy-In attribute noise model, we prove that $l_{0-1}$ is robust for any distribution over 2 dimensional feature space. However, due to computational intractability of $l_{0-1}$, we resort to $l_{sq}$ and observe that it need not be Asy-In noise robust. Our empirical results support Sy-De robustness of squared loss for low to moderate noise rates.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge