Multi-Leader Congestion Games with an Adversary

We study a multi-leader single-follower congestion game where multiple users (leaders) choose one resource out of a set of resources and, after observing the realized loads, an adversary (single-follower) attacks the resources with maximum loads, causing additional costs for the leaders. For the resulting strategic game among the leaders, we show that pure Nash equilibria may fail to exist and therefore, we consider approximate equilibria instead. As our first main result, we show that the existence of a $K$-approximate equilibrium can always be guaranteed, where $K \approx 1.1974$ is the unique solution of a cubic polynomial equation. To this end, we give a polynomial time combinatorial algorithm which computes a $K$-approximate equilibrium. The factor $K$ is tight, meaning that there is an instance that does not admit an $\alpha$-approximate equilibrium for any $\alpha<K$. Thus $\alpha=K$ is the smallest possible value of $\alpha$ such that the existence of an $\alpha$-approximate equilibrium can be guaranteed for any instance of the considered game. Secondly, we focus on approximate equilibria of a given fixed instance. We show how to compute efficiently a best approximate equilibrium, that is, with smallest possible $\alpha$ among all $\alpha$-approximate equilibria of the given instance.

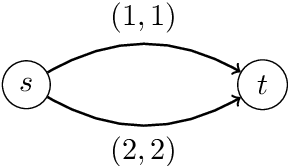
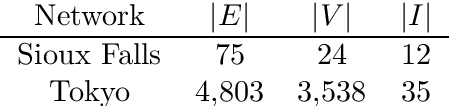
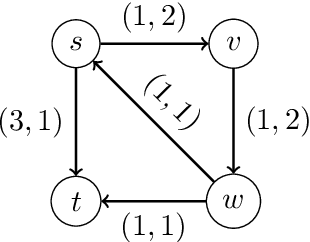
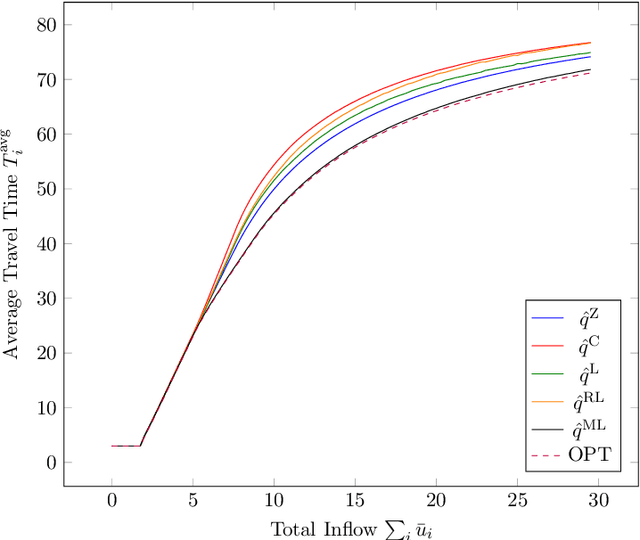
Machine-Learned Prediction Equilibrium for Dynamic Traffic Assignment

We study a dynamic traffic assignment model, where agents base their instantaneous routing decisions on real-time delay predictions. We formulate a mathematically concise model and derive properties of the predictors that ensure a dynamic prediction equilibrium exists. We demonstrate the versatility of our framework by showing that it subsumes the well-known full information and instantaneous information models, in addition to admitting further realistic predictors as special cases. We complement our theoretical analysis by an experimental study, in which we systematically compare the induced average travel times of different predictors, including a machine-learning model trained on data gained from previously computed equilibrium flows, both on a synthetic and a real road network.