Yuan Deng
TNT: Improving Chunkwise Training for Test-Time Memorization
Nov 10, 2025Abstract:Recurrent neural networks (RNNs) with deep test-time memorization modules, such as Titans and TTT, represent a promising, linearly-scaling paradigm distinct from Transformers. While these expressive models do not yet match the peak performance of state-of-the-art Transformers, their potential has been largely untapped due to prohibitively slow training and low hardware utilization. Existing parallelization methods force a fundamental conflict governed by the chunksize hyperparameter: large chunks boost speed but degrade performance, necessitating a fixed, suboptimal compromise. To solve this challenge, we introduce TNT, a novel training paradigm that decouples training efficiency from inference performance through a two-stage process. Stage one is an efficiency-focused pre-training phase utilizing a hierarchical memory. A global module processes large, hardware-friendly chunks for long-range context, while multiple parallel local modules handle fine-grained details. Crucially, by periodically resetting local memory states, we break sequential dependencies to enable massive context parallelization. Stage two is a brief fine-tuning phase where only the local memory modules are adapted to a smaller, high-resolution chunksize, maximizing accuracy with minimal overhead. Evaluated on Titans and TTT models, TNT achieves a substantial acceleration in training speed-up to 17 times faster than the most accurate baseline configuration - while simultaneously improving model accuracy. This improvement removes a critical scalability barrier, establishing a practical foundation for developing expressive RNNs and facilitating future work to close the performance gap with Transformers.
ATLAS: Learning to Optimally Memorize the Context at Test Time
May 29, 2025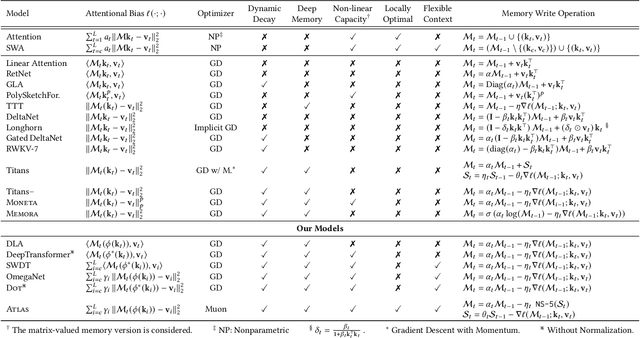
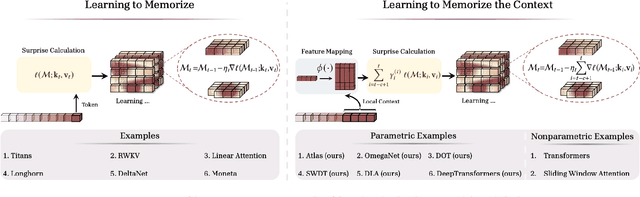
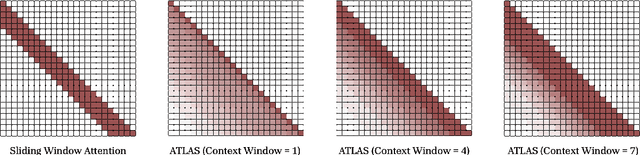
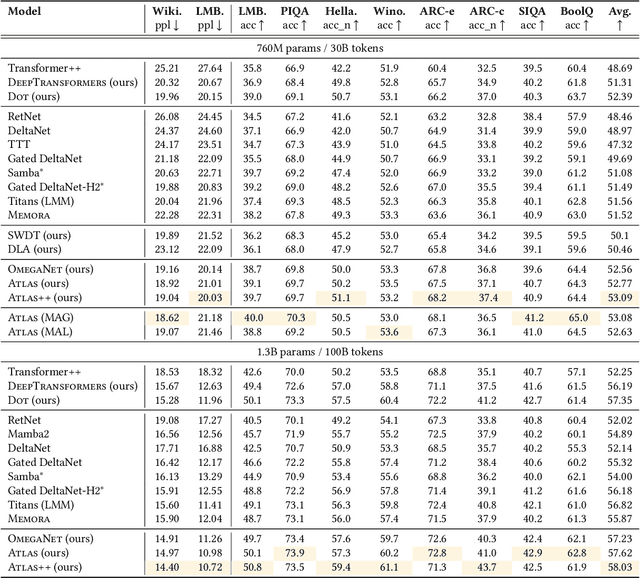
Abstract:Transformers have been established as the most popular backbones in sequence modeling, mainly due to their effectiveness in in-context retrieval tasks and the ability to learn at scale. Their quadratic memory and time complexity, however, bound their applicability in longer sequences and so has motivated researchers to explore effective alternative architectures such as modern recurrent neural networks (a.k.a long-term recurrent memory module). Despite their recent success in diverse downstream tasks, they struggle in tasks that requires long context understanding and extrapolation to longer sequences. We observe that these shortcomings come from three disjoint aspects in their design: (1) limited memory capacity that is bounded by the architecture of memory and feature mapping of the input; (2) online nature of update, i.e., optimizing the memory only with respect to the last input; and (3) less expressive management of their fixed-size memory. To enhance all these three aspects, we present ATLAS, a long-term memory module with high capacity that learns to memorize the context by optimizing the memory based on the current and past tokens, overcoming the online nature of long-term memory models. Building on this insight, we present a new family of Transformer-like architectures, called DeepTransformers, that are strict generalizations of the original Transformer architecture. Our experimental results on language modeling, common-sense reasoning, recall-intensive, and long-context understanding tasks show that ATLAS surpasses the performance of Transformers and recent linear recurrent models. ATLAS further improves the long context performance of Titans, achieving +80\% accuracy in 10M context length of BABILong benchmark.
PiKE: Adaptive Data Mixing for Multi-Task Learning Under Low Gradient Conflicts
Feb 10, 2025Abstract:Modern machine learning models are trained on diverse datasets and tasks to improve generalization. A key challenge in multitask learning is determining the optimal data mixing and sampling strategy across different data sources. Prior research in this multi-task learning setting has primarily focused on mitigating gradient conflicts between tasks. However, we observe that many real-world multitask learning scenarios-such as multilingual training and multi-domain learning in large foundation models-exhibit predominantly positive task interactions with minimal or no gradient conflict. Building on this insight, we introduce PiKE (Positive gradient interaction-based K-task weights Estimator), an adaptive data mixing algorithm that dynamically adjusts task contributions throughout training. PiKE optimizes task sampling to minimize overall loss, effectively leveraging positive gradient interactions with almost no additional computational overhead. We establish theoretical convergence guarantees for PiKE and demonstrate its superiority over static and non-adaptive mixing strategies. Additionally, we extend PiKE to promote fair learning across tasks, ensuring balanced progress and preventing task underrepresentation. Empirical evaluations on large-scale language model pretraining show that PiKE consistently outperforms existing heuristic and static mixing strategies, leading to faster convergence and improved downstream task performance.
Procurement Auctions via Approximately Optimal Submodular Optimization
Nov 20, 2024Abstract:We study procurement auctions, where an auctioneer seeks to acquire services from strategic sellers with private costs. The quality of services is measured by a submodular function known to the auctioneer. Our goal is to design computationally efficient procurement auctions that (approximately) maximize the difference between the quality of the acquired services and the total cost of the sellers, while ensuring incentive compatibility (IC), individual rationality (IR) for sellers, and non-negative surplus (NAS) for the auctioneer. Our contributions are twofold: (i) we provide an improved analysis of existing algorithms for non-positive submodular function maximization, and (ii) we design efficient frameworks that transform submodular optimization algorithms into mechanisms that are IC, IR, NAS, and approximation-preserving. These frameworks apply to both the offline setting, where all sellers' bids and services are available simultaneously, and the online setting, where sellers arrive in an adversarial order, requiring the auctioneer to make irrevocable decisions. We also explore whether state-of-the-art submodular optimization algorithms can be converted into descending auctions in adversarial settings, where the schedule of descending prices is determined by an adversary. We show that a submodular optimization algorithm satisfying bi-criteria $(1/2, 1)$-approximation in welfare can be effectively adapted to a descending auction. Additionally, we establish a connection between descending auctions and online submodular optimization. Finally, we demonstrate the practical applications of our frameworks by instantiating them with state-of-the-art submodular optimization algorithms and empirically comparing their welfare performance on publicly available datasets with thousands of sellers.
Addax: Utilizing Zeroth-Order Gradients to Improve Memory Efficiency and Performance of SGD for Fine-Tuning Language Models
Oct 09, 2024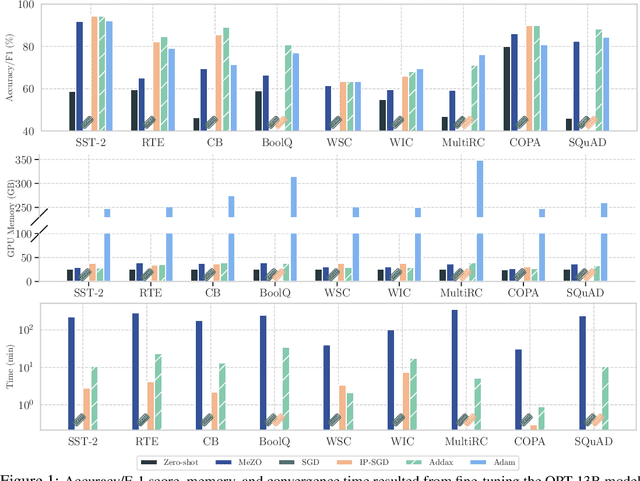

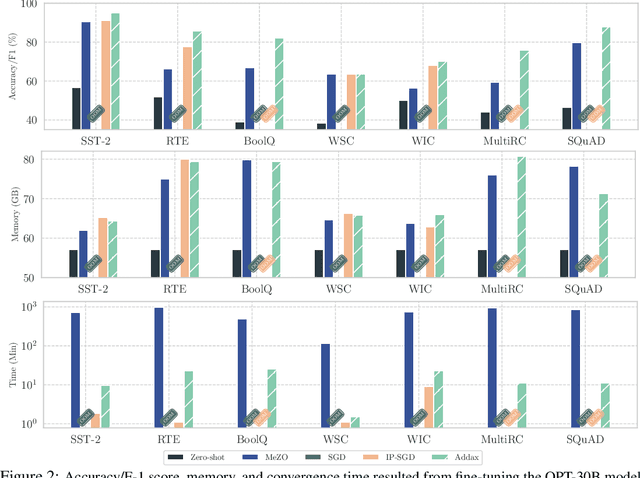

Abstract:Fine-tuning language models (LMs) with the Adam optimizer often demands excessive memory, limiting accessibility. The "in-place" version of Stochastic Gradient Descent (IP-SGD) and Memory-Efficient Zeroth-order Optimizer (MeZO) have been proposed to address this. However, IP-SGD still requires substantial memory, and MeZO suffers from slow convergence and degraded final performance due to its zeroth-order nature. This paper introduces Addax, a novel method that improves both memory efficiency and performance of IP-SGD by integrating it with MeZO. Specifically, Addax computes zeroth- or first-order gradients of data points in the minibatch based on their memory consumption, combining these gradient estimates to update directions. By computing zeroth-order gradients for data points that require more memory and first-order gradients for others, Addax overcomes the slow convergence of MeZO and the excessive memory requirement of IP-SGD. Additionally, the zeroth-order gradient acts as a regularizer for the first-order gradient, further enhancing the model's final performance. Theoretically, we establish the convergence of Addax under mild assumptions, demonstrating faster convergence and less restrictive hyper-parameter choices than MeZO. Our experiments with diverse LMs and tasks show that Addax consistently outperforms MeZO regarding accuracy and convergence speed while having a comparable memory footprint. When fine-tuning OPT-13B with one A100 GPU, on average, Addax outperforms MeZO in accuracy/F1 score by 14% and runs 15x faster while using memory similar to MeZO. In our experiments on the larger OPT-30B model, on average, Addax outperforms MeZO in terms of accuracy/F1 score by >16 and runs 30x faster on a single H100 GPU. Moreover, Addax surpasses the performance of standard fine-tuning approaches, such as IP-SGD and Adam, in most tasks with significantly less memory requirement.
Multi-channel Autobidding with Budget and ROI Constraints
Feb 13, 2023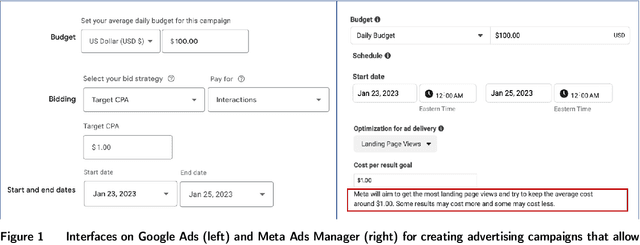
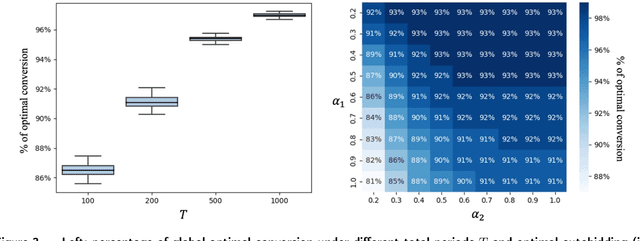
Abstract:In digital online advertising, advertisers procure ad impressions simultaneously on multiple platforms, or so-called channels, such as Google Ads, Meta Ads Manager, etc., each of which consists of numerous ad auctions. We study how an advertiser maximizes total conversion (e.g. ad clicks) while satisfying aggregate return-on-investment (ROI) and budget constraints across all channels. In practice, an advertiser does not have control over, and thus cannot globally optimize, which individual ad auctions she participates in for each channel, and instead authorizes a channel to procure impressions on her behalf: the advertiser can only utilize two levers on each channel, namely setting a per-channel budget and per-channel target ROI. In this work, we first analyze the effectiveness of each of these levers for solving the advertiser's global multi-channel problem. We show that when an advertiser only optimizes over per-channel ROIs, her total conversion can be arbitrarily worse than what she could have obtained in the global problem. Further, we show that the advertiser can achieve the global optimal conversion when she only optimizes over per-channel budgets. In light of this finding, under a bandit feedback setting that mimics real-world scenarios where advertisers have limited information on ad auctions in each channels and how channels procure ads, we present an efficient learning algorithm that produces per-channel budgets whose resulting conversion approximates that of the global optimal problem. Finally, we argue that all our results hold for both single-item and multi-item auctions from which channels procure impressions on advertisers' behalf.
Strategizing against No-regret Learners
Sep 30, 2019Abstract:How should a player who repeatedly plays a game against a no-regret learner strategize to maximize his utility? We study this question and show that under some mild assumptions, the player can always guarantee himself a utility of at least what he would get in a Stackelberg equilibrium of the game. When the no-regret learner has only two actions, we show that the player cannot get any higher utility than the Stackelberg equilibrium utility. But when the no-regret learner has more than two actions and plays a mean-based no-regret strategy, we show that the player can get strictly higher than the Stackelberg equilibrium utility. We provide a characterization of the optimal game-play for the player against a mean-based no-regret learner as a solution to a control problem. When the no-regret learner's strategy also guarantees him a no-swap regret, we show that the player cannot get anything higher than a Stackelberg equilibrium utility.
Homotopy Analysis for Tensor PCA
Jun 14, 2017



Abstract:Developing efficient and guaranteed nonconvex algorithms has been an important challenge in modern machine learning. Algorithms with good empirical performance such as stochastic gradient descent often lack theoretical guarantees. In this paper, we analyze the class of homotopy or continuation methods for global optimization of nonconvex functions. These methods start from an objective function that is efficient to optimize (e.g. convex), and progressively modify it to obtain the required objective, and the solutions are passed along the homotopy path. For the challenging problem of tensor PCA, we prove global convergence of the homotopy method in the "high noise" regime. The signal-to-noise requirement for our algorithm is tight in the sense that it matches the recovery guarantee for the best degree-4 sum-of-squares algorithm. In addition, we prove a phase transition along the homotopy path for tensor PCA. This allows to simplify the homotopy method to a local search algorithm, viz., tensor power iterations, with a specific initialization and a noise injection procedure, while retaining the theoretical guarantees.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge