Online Ad Procurement in Non-stationary Autobidding Worlds

Today's online advertisers procure digital ad impressions through interacting with autobidding platforms: advertisers convey high level procurement goals via setting levers such as budget, target return-on-investment, max cost per click, etc.. Then ads platforms subsequently procure impressions on advertisers' behalf, and report final procurement conversions (e.g. click) to advertisers. In practice, advertisers may receive minimal information on platforms' procurement details, and procurement outcomes are subject to non-stationary factors like seasonal patterns, occasional system corruptions, and market trends which make it difficult for advertisers to optimize lever decisions effectively. Motivated by this, we present an online learning framework that helps advertisers dynamically optimize ad platform lever decisions while subject to general long-term constraints in a realistic bandit feedback environment with non-stationary procurement outcomes. In particular, we introduce a primal-dual algorithm for online decision making with multi-dimension decision variables, bandit feedback and long-term uncertain constraints. We show that our algorithm achieves low regret in many worlds when procurement outcomes are generated through procedures that are stochastic, adversarial, adversarially corrupted, periodic, and ergodic, respectively, without having to know which procedure is the ground truth. Finally, we emphasize that our proposed algorithm and theoretical results extend beyond the applications of online advertising.

Interpolating Item and User Fairness in Recommendation Systems

Online platforms employ recommendation systems to enhance customer engagement and drive revenue. However, in a multi-sided platform where the platform interacts with diverse stakeholders such as sellers (items) and customers (users), each with their own desired outcomes, finding an appropriate middle ground becomes a complex operational challenge. In this work, we investigate the ``price of fairness'', which captures the platform's potential compromises when balancing the interests of different stakeholders. Motivated by this, we propose a fair recommendation framework where the platform maximizes its revenue while interpolating between item and user fairness constraints. We further examine the fair recommendation problem in a more realistic yet challenging online setting, where the platform lacks knowledge of user preferences and can only observe binary purchase decisions. To address this, we design a low-regret online optimization algorithm that preserves the platform's revenue while achieving fairness for both items and users. Finally, we demonstrate the effectiveness of our framework and proposed method via a case study on MovieLens data.

Multi-channel Autobidding with Budget and ROI Constraints

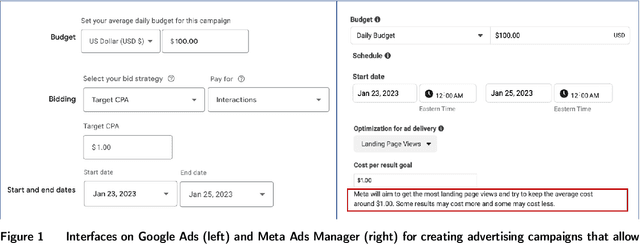
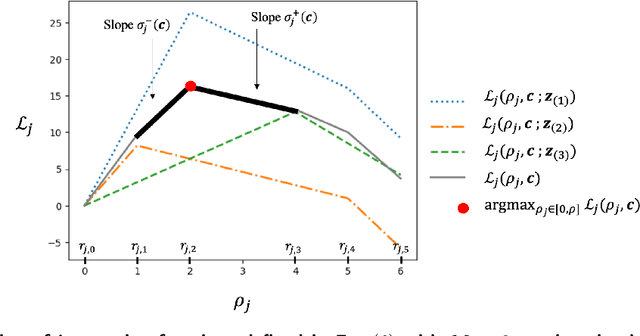
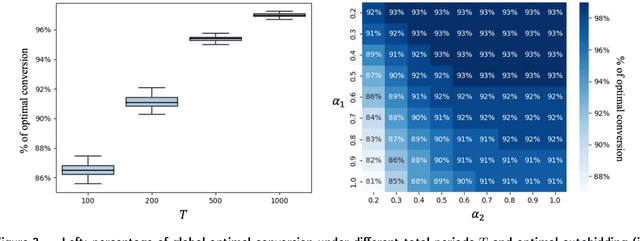
In digital online advertising, advertisers procure ad impressions simultaneously on multiple platforms, or so-called channels, such as Google Ads, Meta Ads Manager, etc., each of which consists of numerous ad auctions. We study how an advertiser maximizes total conversion (e.g. ad clicks) while satisfying aggregate return-on-investment (ROI) and budget constraints across all channels. In practice, an advertiser does not have control over, and thus cannot globally optimize, which individual ad auctions she participates in for each channel, and instead authorizes a channel to procure impressions on her behalf: the advertiser can only utilize two levers on each channel, namely setting a per-channel budget and per-channel target ROI. In this work, we first analyze the effectiveness of each of these levers for solving the advertiser's global multi-channel problem. We show that when an advertiser only optimizes over per-channel ROIs, her total conversion can be arbitrarily worse than what she could have obtained in the global problem. Further, we show that the advertiser can achieve the global optimal conversion when she only optimizes over per-channel budgets. In light of this finding, under a bandit feedback setting that mimics real-world scenarios where advertisers have limited information on ad auctions in each channels and how channels procure ads, we present an efficient learning algorithm that produces per-channel budgets whose resulting conversion approximates that of the global optimal problem. Finally, we argue that all our results hold for both single-item and multi-item auctions from which channels procure impressions on advertisers' behalf.

Decision Trees for Decision-Making under the Predict-then-Optimize Framework

We consider the use of decision trees for decision-making problems under the predict-then-optimize framework. That is, we would like to first use a decision tree to predict unknown input parameters of an optimization problem, and then make decisions by solving the optimization problem using the predicted parameters. A natural loss function in this framework is to measure the suboptimality of the decisions induced by the predicted input parameters, as opposed to measuring loss using input parameter prediction error. This natural loss function is known in the literature as the Smart Predict-then-Optimize (SPO) loss, and we propose a tractable methodology called SPO Trees (SPOTs) for training decision trees under this loss. SPOTs benefit from the interpretability of decision trees, providing an interpretable segmentation of contextual features into groups with distinct optimal solutions to the optimization problem of interest. We conduct several numerical experiments on synthetic and real data including the prediction of travel times for shortest path problems and predicting click probabilities for news article recommendation. We demonstrate on these datasets that SPOTs simultaneously provide higher quality decisions and significantly lower model complexity than other machine learning approaches (e.g., CART) trained to minimize prediction error.

Incentive-aware Contextual Pricing with Non-parametric Market Noise

We consider a dynamic pricing problem for repeated contextual second-price auctions with strategic buyers whose goals are to maximize their long-term time discounted utility. The seller has very limited information about buyers' overall demand curves, which depends on $d$-dimensional context vectors characterizing auctioned items, and a non-parametric market noise distribution that captures buyers' idiosyncratic tastes. The noise distribution and the relationship between the context vectors and buyers' demand curves are both unknown to the seller. We focus on designing the seller's learning policy to set contextual reserve prices where the seller's goal is to minimize his regret for revenue. We first propose a pricing policy when buyers are truthful and show that it achieves a $T$-period regret bound of $\tilde{\mathcal{O}}(\sqrt{dT})$ against a clairvoyant policy that has full information of the buyers' demand. Next, under the setting where buyers bid strategically to maximize their long-term discounted utility, we develop a variant of our first policy that is robust to strategic (corrupted) bids. This policy incorporates randomized "isolation" periods, during which a buyer is randomly chosen to solely participate in the auction. We show that this design allows the seller to control the number of periods in which buyers significantly corrupt their bids. Because of this nice property, our robust policy enjoys a $T$-period regret of $\tilde{\mathcal{O}}(\sqrt{dT})$, matching that under the truthful setting up to a constant factor that depends on the utility discount factor.