MPAX: Mathematical Programming in JAX

We introduce MPAX (Mathematical Programming in JAX), a versatile and efficient toolbox for integrating mathematical programming into machine learning workflows. MPAX implemented firstorder methods in JAX, providing native support for hardware accelerations along with features like batch solving, auto-differentiation, and device parallelism. Currently in beta version, MPAX supports linear programming and will be extended to solve more general mathematical programming problems and specialized modules for common machine learning tasks. The solver is available at https://github.com/MIT-Lu-Lab/MPAX.

Online Ad Procurement in Non-stationary Autobidding Worlds

Today's online advertisers procure digital ad impressions through interacting with autobidding platforms: advertisers convey high level procurement goals via setting levers such as budget, target return-on-investment, max cost per click, etc.. Then ads platforms subsequently procure impressions on advertisers' behalf, and report final procurement conversions (e.g. click) to advertisers. In practice, advertisers may receive minimal information on platforms' procurement details, and procurement outcomes are subject to non-stationary factors like seasonal patterns, occasional system corruptions, and market trends which make it difficult for advertisers to optimize lever decisions effectively. Motivated by this, we present an online learning framework that helps advertisers dynamically optimize ad platform lever decisions while subject to general long-term constraints in a realistic bandit feedback environment with non-stationary procurement outcomes. In particular, we introduce a primal-dual algorithm for online decision making with multi-dimension decision variables, bandit feedback and long-term uncertain constraints. We show that our algorithm achieves low regret in many worlds when procurement outcomes are generated through procedures that are stochastic, adversarial, adversarially corrupted, periodic, and ergodic, respectively, without having to know which procedure is the ground truth. Finally, we emphasize that our proposed algorithm and theoretical results extend beyond the applications of online advertising.

From Online Optimization to PID Controllers: Mirror Descent with Momentum

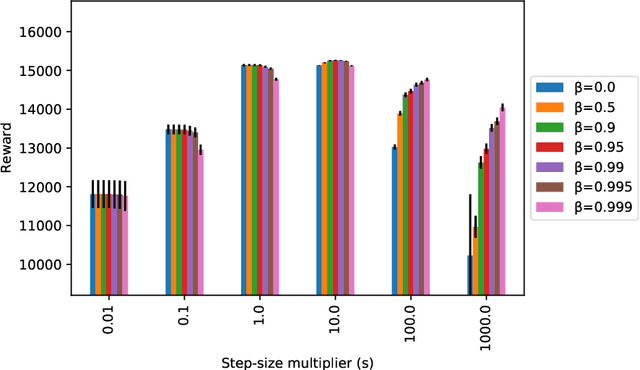
We study a family of first-order methods with momentum based on mirror descent for online convex optimization, which we dub online mirror descent with momentum (OMDM). Our algorithms include as special cases gradient descent and exponential weights update with momentum. We provide a new and simple analysis of momentum-based methods in a stochastic setting that yields a regret bound that decreases as momentum increases. This immediately establishes that momentum can help in the convergence of stochastic subgradient descent in convex nonsmooth optimization. We showcase the robustness of our algorithm by also providing an analysis in an adversarial setting that gives the first non-trivial regret bounds for OMDM. Our work aims to provide a better understanding of the benefits of momentum-based methods, which despite their recent empirical success, is incomplete. Finally, we discuss how OMDM can be applied to stochastic online allocation problems, which are central problems in computer science and operations research. In doing so, we establish an important connection between OMDM and popular approaches from optimal control such as PID controllers, thereby providing regret bounds on the performance of PID controllers. The improvements of momentum are most pronounced when the step-size is large, thereby indicating that momentum provides a robustness to misspecification of tuning parameters. We provide a numerical evaluation that verifies the robustness of our algorithms.

Linear Convergence of Stochastic Primal Dual Methods for Linear Programming Using Variance Reduction and Restarts

There is a recent interest on first-order methods for linear programming (LP). In this paper, we propose a stochastic algorithm using variance reduction and restarts for solving sharp primal-dual problems such as LP. We show that the proposed stochastic method exhibits a linear convergence rate for sharp instances with a high probability, which improves the complexity of the existing deterministic and stochastic algorithms. In addition, we propose an efficient coordinate-based stochastic oracle for unconstrained bilinear problems, which has $\mathcal O(1)$ per iteration cost and improves the total flop counts to reach a certain accuracy.

The Best of Many Worlds: Dual Mirror Descent for Online Allocation Problems

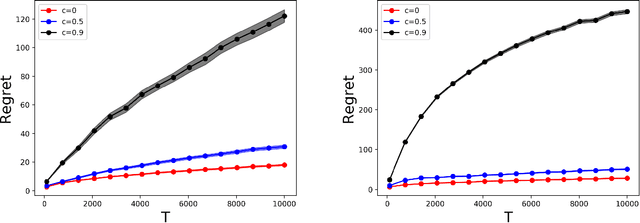
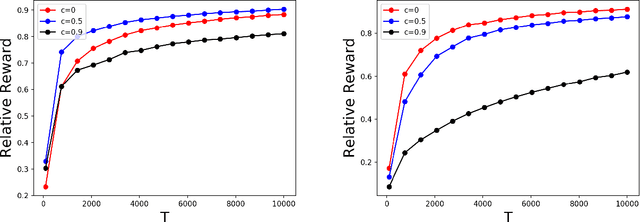
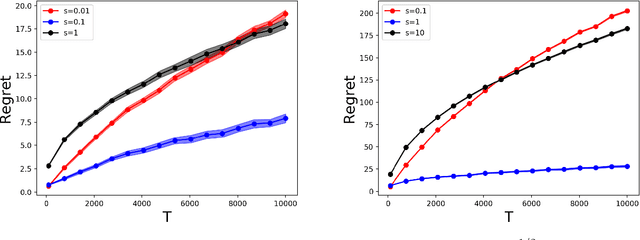
Online allocation problems with resource constraints are central problems in revenue management and online advertising. In these problems, requests arrive sequentially during a finite horizon and, for each request, a decision maker needs to choose an action that consumes a certain amount of resources and generates reward. The objective is to maximize cumulative rewards subject to a constraint on the total consumption of resources. In this paper, we consider a data-driven setting in which the reward and resource consumption of each request are generated using an input model that is unknown to the decision maker. We design a general class of algorithms that attain good performance in various inputs models without knowing which type of input they are facing. In particular, our algorithms are asymptotically optimal under stochastic i.i.d. input model as well as various non-stationary stochastic input models, and they attain an asymptotically optimal fixed competitive ratio when the input is adversarial. Our algorithms operate in the Lagrangian dual space: they maintain a dual multiplier for each resource that is updated using online mirror descent. By choosing the reference function accordingly, we recover dual sub-gradient descent and dual exponential weights algorithm. The resulting algorithms are simple, fast, and have minimal requirements on the reward functions, consumption functions and the action space, in contrast to existing methods for online allocation problems. We discuss applications to network revenue management, online bidding in repeated auctions with budget constraints, online proportional matching with high entropy, and personalized assortment optimization with limited inventories.

Limiting Behaviors of Nonconvex-Nonconcave Minimax Optimization via Continuous-Time Systems

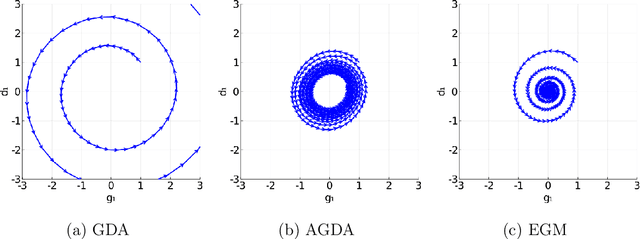
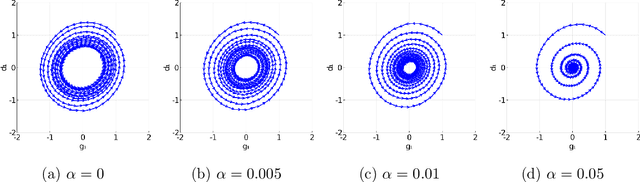
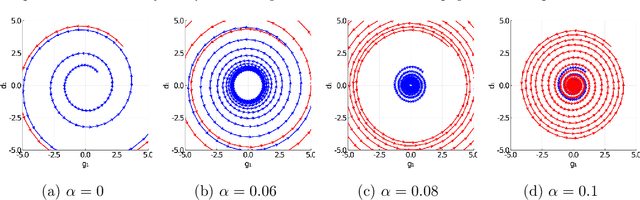
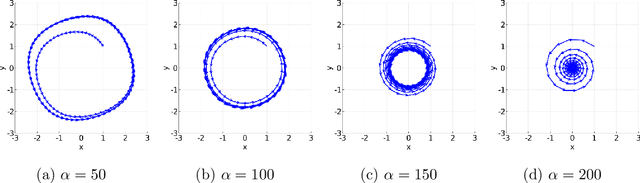
Unlike nonconvex optimization, where gradient descent is guaranteed to converge to a local optimizer, algorithms for nonconvex-nonconcave minimax optimization can have topologically different solution paths: sometimes converging to a solution, sometimes never converging and instead following a limit cycle, and sometimes diverging. In this paper, we study the limiting behaviors of three classic minimax algorithms: gradient decent ascent (GDA), alternating gradient decent ascent (AGDA), and the extragradient method (EGM). Numerically, we observe that all of these limiting behaviors can arise in Generative Adversarial Networks (GAN) training. To explain these different behaviors, we study the high-order resolution continuous-time dynamics that correspond to each algorithm, which results in the sufficient (and almost necessary) conditions for the local convergence by each method. Moreover, this ODE perspective allows us to characterize the phase transition between these different limiting behaviors caused by introducing regularization in the problem instance.

Regularized Online Allocation Problems: Fairness and Beyond

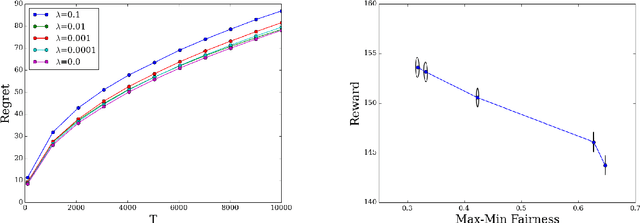
Online allocation problems with resource constraints have a rich history in computer science and operations research. In this paper, we introduce the \emph{regularized online allocation problem}, a variant that includes a non-linear regularizer acting on the total resource consumption. In this problem, requests repeatedly arrive over time and, for each request, a decision maker needs to take an action that generates a reward and consumes resources. The objective is to simultaneously maximize total rewards and the value of the regularizer subject to the resource constraints. Our primary motivation is the online allocation of internet advertisements wherein firms seek to maximize additive objectives such as the revenue or efficiency of the allocation. By introducing a regularizer, firms can account for the fairness of the allocation or, alternatively, punish under-delivery of advertisements---two common desiderata in internet advertising markets. We design an algorithm when arrivals are drawn independently from a distribution that is unknown to the decision maker. Our algorithm is simple, fast, and attains the optimal order of sub-linear regret compared to the optimal allocation with the benefit of hindsight. Numerical experiments confirm the effectiveness of the proposed algorithm and of the regularizers in an internet advertising application.

The Landscape of Nonconvex-Nonconcave Minimax Optimization

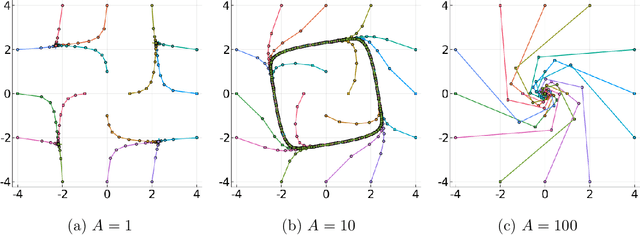
Minimax optimization has become a central tool for modern machine learning with applications in robust optimization, game theory and training GANs. These applications are often nonconvex-nonconcave, but the existing theory is unable to identify and deal with the fundamental difficulties posed by nonconvex-nonconcave structures. We break this historical barrier by identifying three regions of nonconvex-nonconcave bilinear minimax problems and characterizing their different solution paths. For problems where the interaction between the agents is sufficiently strong, we derive global linear convergence guarantees. Conversely when the interaction between the agents is fairly weak, we derive local linear convergence guarantees. Between these two settings, we show that limiting cycles may occur, preventing the convergence of the solution path.

Contextual Reserve Price Optimization in Auctions

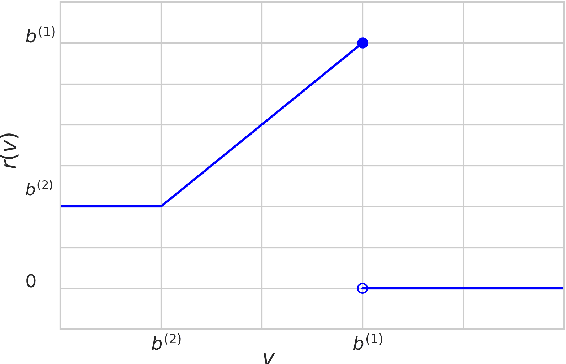
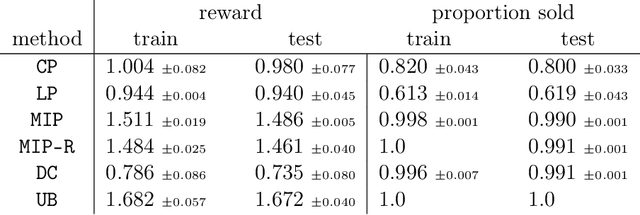
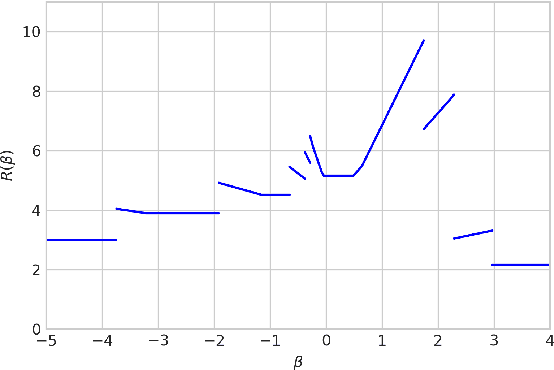
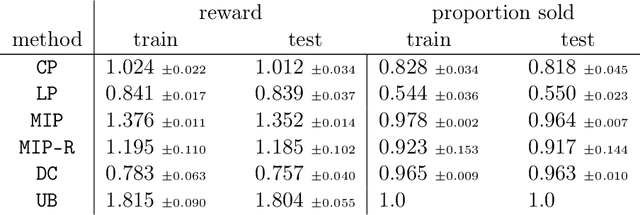
We study the problem of learning a linear model to set the reserve price in order to maximize expected revenue in an auction, given contextual information. First, we show that it is not possible to solve this problem in polynomial time unless the \emph{Exponential Time Hypothesis} fails. Second, we present a strong mixed-integer programming (MIP) formulation for this problem, which is capable of exactly modeling the nonconvex and discontinuous expected reward function. Moreover, we show that this MIP formulation is ideal (the strongest possible formulation) for the revenue function. Since it can be computationally expensive to exactly solve the MIP formulation, we also study the performance of its linear programming (LP) relaxation. We show that, unfortunately, in the worst case the objective gap of the linear programming relaxation can be $O(n)$ times larger than the optimal objective of the actual problem, where $n$ is the number of samples. Finally, we present computational results, showcasing that the mixed-integer programming formulation, along with its linear programming relaxation, are able to superior both the in-sample performance and the out-of-sample performance of the state-of-the-art algorithms on both real and synthetic datasets.

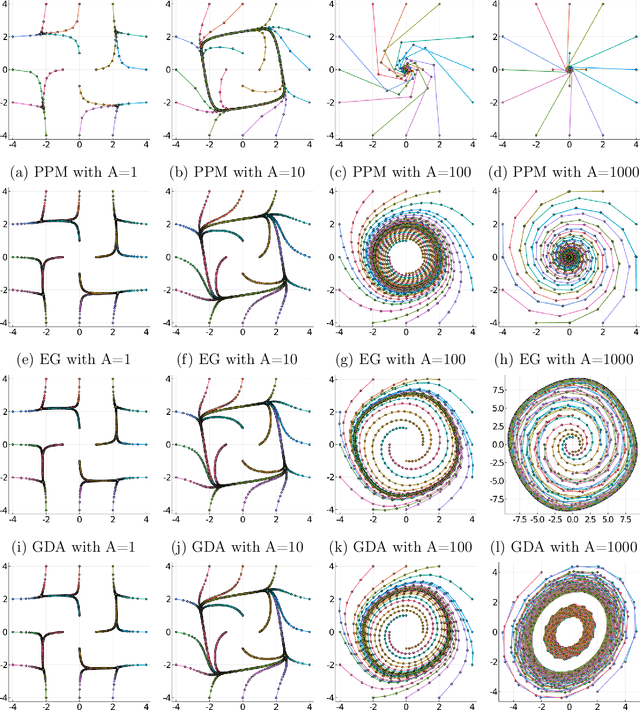
An $O$-Resolution ODE Framework for Discrete-Time Optimization Algorithms and Applications to Convex-Concave Saddle-Point Problems

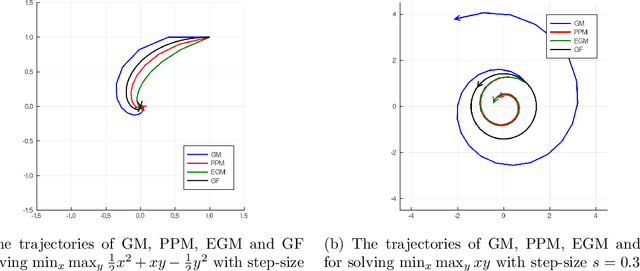
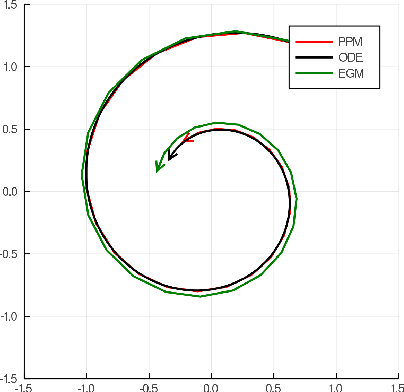
There has been a long history of using Ordinary Differential Equations (ODEs) to understand the dynamic of discrete-time optimization algorithms. However, one major difficulty of applying this approach is that there can be multiple ODEs that correspond to the same discrete-time algorithm, depending on how to take the continuous limit, which makes it unclear how to obtain the suitable ODE from a discrete-time optimization algorithm. Inspired by the recent paper \cite{shi2018understanding}, we propose the $r$-th degree ODE expansion of a discrete-time optimization algorithm, which provides a principal approach to construct the unique $O(s^r)$-resolution ODE systems for a given discrete-time algorithm, where $s$ is the step-size of the algorithm. We utilize this machinery to study three classic algorithms -- gradient method (GM), proximal point method (PPM) and extra-gradient method (EGM) -- for finding the solution to the unconstrained convex-concave saddle-point problem $\min_{x\in\RR^n} \max_{y\in \RR^m} L(x,y)$, which explains their puzzling convergent/divergent behaviors when $L(x,y)$ is a bilinear function. Moreover, their $O(s)$-resolution ODEs inspire us to define the $O(s)$-linear-convergence condition on $L(x,y)$, under which PPM and EGM exhabit linear convergence. This condition not only unifies the known linear convergence rate of PPM and EGM, but also showcases that these two algorithms exhibit linear convergence in broader contexts.