Limiting Behaviors of Nonconvex-Nonconcave Minimax Optimization via Continuous-Time Systems
Paper and Code
Oct 20, 2020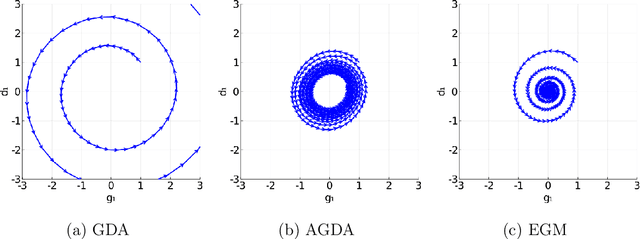
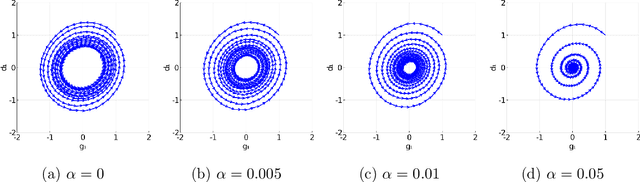
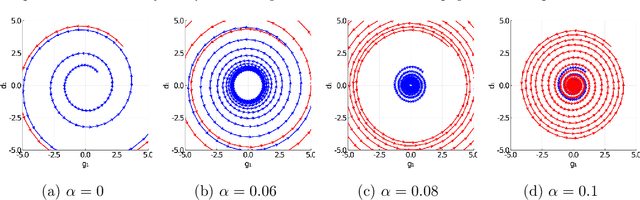
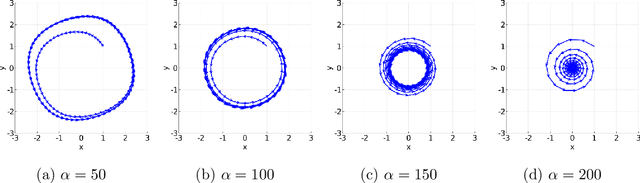
Unlike nonconvex optimization, where gradient descent is guaranteed to converge to a local optimizer, algorithms for nonconvex-nonconcave minimax optimization can have topologically different solution paths: sometimes converging to a solution, sometimes never converging and instead following a limit cycle, and sometimes diverging. In this paper, we study the limiting behaviors of three classic minimax algorithms: gradient decent ascent (GDA), alternating gradient decent ascent (AGDA), and the extragradient method (EGM). Numerically, we observe that all of these limiting behaviors can arise in Generative Adversarial Networks (GAN) training. To explain these different behaviors, we study the high-order resolution continuous-time dynamics that correspond to each algorithm, which results in the sufficient (and almost necessary) conditions for the local convergence by each method. Moreover, this ODE perspective allows us to characterize the phase transition between these different limiting behaviors caused by introducing regularization in the problem instance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge