Pratik Worah
Sampling and Loss Weights in Multi-Domain Training
Nov 10, 2025Abstract:In the training of large deep neural networks, there is a need for vast amounts of training data. To meet this need, data is collected from multiple domains, such as Wikipedia and GitHub. These domains are heterogeneous in both data quality and the diversity of information they provide. This raises the question of how much we should rely on each domain. Several methods have attempted to address this issue by assigning sampling weights to each data domain using heuristics or approximations. As a first step toward a deeper understanding of the role of data mixing, this work revisits the problem by studying two kinds of weights: sampling weights, which control how much each domain contributes in a batch, and loss weights, which scale the loss from each domain during training. Through a rigorous study of linear regression, we show that these two weights play complementary roles. First, they can reduce the variance of gradient estimates in iterative methods such as stochastic gradient descent (SGD). Second, they can improve generalization performance by reducing the generalization gap. We provide both theoretical and empirical support for these claims. We further study the joint dynamics of sampling weights and loss weights, examining how they can be combined to capture both contributions.
A Goemans-Williamson type algorithm for identifying subcohorts in clinical trials
Jun 12, 2025Abstract:We design an efficient algorithm that outputs a linear classifier for identifying homogeneous subsets (equivalently subcohorts) from large inhomogeneous datasets. Our theoretical contribution is a rounding technique, similar to that of Goemans and Williamson (1994), that approximates the optimal solution of the underlying optimization problem within a factor of $0.82$. As an application, we use our algorithm to design a simple test that can identify homogeneous subcohorts of patients, that are mainly comprised of metastatic cases, from the RNA microarray dataset for breast cancer by Curtis et al. (2012). Furthermore, we also use the test output by the algorithm to systematically identify subcohorts of patients in which statistically significant changes in methylation levels of tumor suppressor genes co-occur with statistically significant changes in nuclear receptor expression. Identifying such homogeneous subcohorts of patients can be useful for the discovery of disease pathways and therapeutics, specific to the subcohort.
Allocating Variance to Maximize Expectation
Feb 25, 2025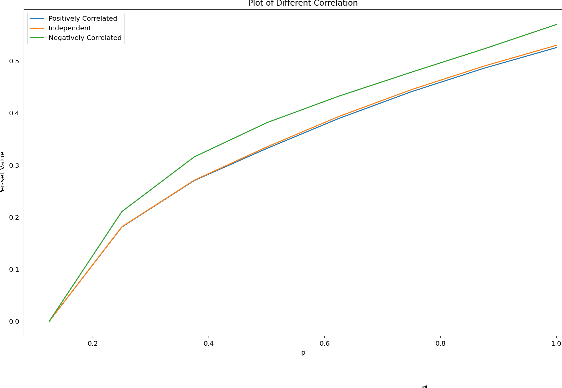
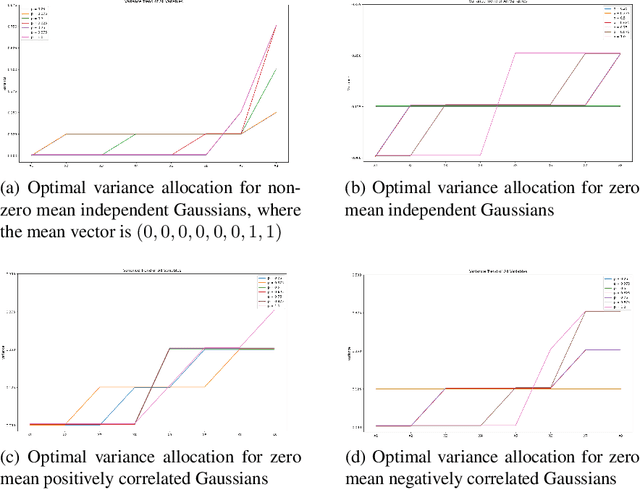
Abstract:We design efficient approximation algorithms for maximizing the expectation of the supremum of families of Gaussian random variables. In particular, let $\mathrm{OPT}:=\max_{\sigma_1,\cdots,\sigma_n}\mathbb{E}\left[\sum_{j=1}^{m}\max_{i\in S_j} X_i\right]$, where $X_i$ are Gaussian, $S_j\subset[n]$ and $\sum_i\sigma_i^2=1$, then our theoretical results include: - We characterize the optimal variance allocation -- it concentrates on a small subset of variables as $|S_j|$ increases, - A polynomial time approximation scheme (PTAS) for computing $\mathrm{OPT}$ when $m=1$, and - An $O(\log n)$ approximation algorithm for computing $\mathrm{OPT}$ for general $m>1$. Such expectation maximization problems occur in diverse applications, ranging from utility maximization in auctions markets to learning mixture models in quantitative genetics.
Enhancing selectivity using Wasserstein distance based reweighing
Jan 21, 2024Abstract:Given two labeled data-sets $\mathcal{S}$ and $\mathcal{T}$, we design a simple and efficient greedy algorithm to reweigh the loss function such that the limiting distribution of the neural network weights that result from training on $\mathcal{S}$ approaches the limiting distribution that would have resulted by training on $\mathcal{T}$. On the theoretical side, we prove that when the metric entropy of the input data-sets is bounded, our greedy algorithm outputs a close to optimal reweighing, i.e., the two invariant distributions of network weights will be provably close in total variation distance. Moreover, the algorithm is simple and scalable, and we prove bounds on the efficiency of the algorithm as well. Our algorithm can deliberately introduce distribution shift to perform (soft) multi-criteria optimization. As a motivating application, we train a neural net to recognize small molecule binders to MNK2 (a MAP Kinase, responsible for cell signaling) which are non-binders to MNK1 (a highly similar protein). We tune the algorithm's parameter so that overall change in holdout loss is negligible, but the selectivity, i.e., the fraction of top 100 MNK2 binders that are MNK1 non-binders, increases from 54\% to 95\%, as a result of our reweighing. Of the 43 distinct small molecules predicted to be most selective from the enamine catalog, 2 small molecules were experimentally verified to be selective, i.e., they reduced the enzyme activity of MNK2 below 50\% but not MNK1, at 10$\mu$M -- a 5\% success rate.
Learning Rate Schedules in the Presence of Distribution Shift
Mar 27, 2023Abstract:We design learning rate schedules that minimize regret for SGD-based online learning in the presence of a changing data distribution. We fully characterize the optimal learning rate schedule for online linear regression via a novel analysis with stochastic differential equations. For general convex loss functions, we propose new learning rate schedules that are robust to distribution shift, and we give upper and lower bounds for the regret that only differ by constants. For non-convex loss functions, we define a notion of regret based on the gradient norm of the estimated models and propose a learning schedule that minimizes an upper bound on the total expected regret. Intuitively, one expects changing loss landscapes to require more exploration, and we confirm that optimal learning rate schedules typically increase in the presence of distribution shift. Finally, we provide experiments for high-dimensional regression models and neural networks to illustrate these learning rate schedules and their cumulative regret.
Learning to Price Against a Moving Target
Jun 08, 2021Abstract:In the Learning to Price setting, a seller posts prices over time with the goal of maximizing revenue while learning the buyer's valuation. This problem is very well understood when values are stationary (fixed or iid). Here we study the problem where the buyer's value is a moving target, i.e., they change over time either by a stochastic process or adversarially with bounded variation. In either case, we provide matching upper and lower bounds on the optimal revenue loss. Since the target is moving, any information learned soon becomes out-dated, which forces the algorithms to keep switching between exploring and exploiting phases.
Limiting Behaviors of Nonconvex-Nonconcave Minimax Optimization via Continuous-Time Systems
Oct 20, 2020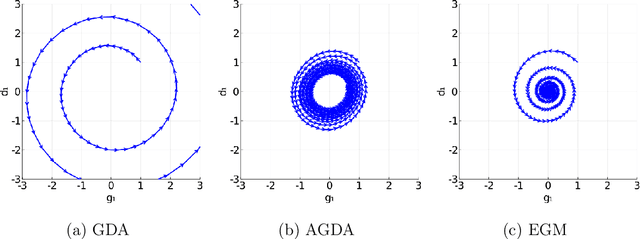
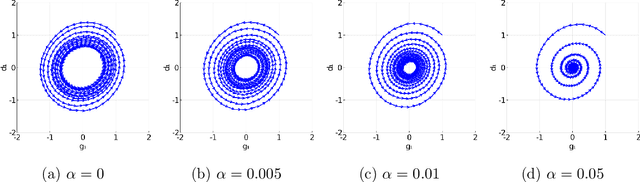
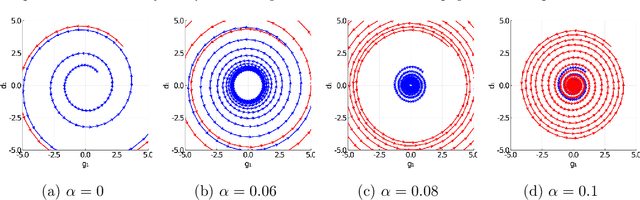
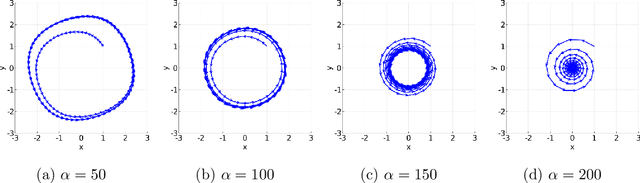
Abstract:Unlike nonconvex optimization, where gradient descent is guaranteed to converge to a local optimizer, algorithms for nonconvex-nonconcave minimax optimization can have topologically different solution paths: sometimes converging to a solution, sometimes never converging and instead following a limit cycle, and sometimes diverging. In this paper, we study the limiting behaviors of three classic minimax algorithms: gradient decent ascent (GDA), alternating gradient decent ascent (AGDA), and the extragradient method (EGM). Numerically, we observe that all of these limiting behaviors can arise in Generative Adversarial Networks (GAN) training. To explain these different behaviors, we study the high-order resolution continuous-time dynamics that correspond to each algorithm, which results in the sufficient (and almost necessary) conditions for the local convergence by each method. Moreover, this ODE perspective allows us to characterize the phase transition between these different limiting behaviors caused by introducing regularization in the problem instance.
The Landscape of Nonconvex-Nonconcave Minimax Optimization
Jun 15, 2020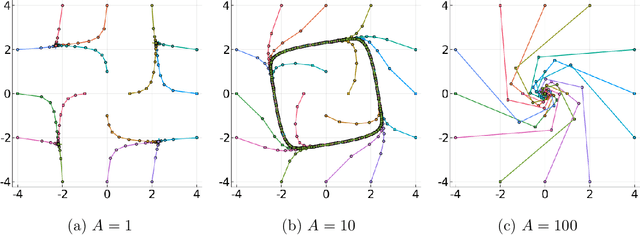
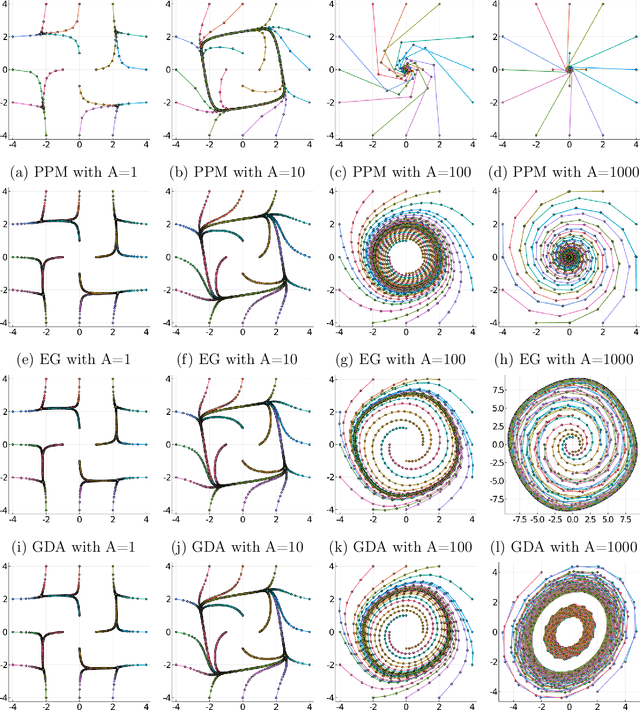
Abstract:Minimax optimization has become a central tool for modern machine learning with applications in robust optimization, game theory and training GANs. These applications are often nonconvex-nonconcave, but the existing theory is unable to identify and deal with the fundamental difficulties posed by nonconvex-nonconcave structures. We break this historical barrier by identifying three regions of nonconvex-nonconcave bilinear minimax problems and characterizing their different solution paths. For problems where the interaction between the agents is sufficiently strong, we derive global linear convergence guarantees. Conversely when the interaction between the agents is fairly weak, we derive local linear convergence guarantees. Between these two settings, we show that limiting cycles may occur, preventing the convergence of the solution path.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge