Provably Faster Gradient Descent via Long Steps

This work establishes provably faster convergence rates for gradient descent in smooth convex optimization via a computer-assisted analysis technique. Our theory allows nonconstant stepsize policies with frequent long steps potentially violating descent by analyzing the overall effect of many iterations at once rather than the typical one-iteration inductions used in most first-order method analyses. We show that long steps, which may increase the objective value in the short term, lead to provably faster convergence in the long term. A conjecture towards proving a faster $O(1/T\log T)$ rate for gradient descent is also motivated along with simple numerical validation.

Some Primal-Dual Theory for Subgradient Methods for Strongly Convex Optimization

We consider (stochastic) subgradient methods for strongly convex but potentially nonsmooth non-Lipschitz optimization. We provide new equivalent dual descriptions (in the style of dual averaging) for the classic subgradient method, the proximal subgradient method, and the switching subgradient method. These equivalences enable $O(1/T)$ convergence guarantees in terms of both their classic primal gap and a not previously analyzed dual gap for strongly convex optimization. Consequently, our theory provides these classic methods with simple, optimal stopping criteria and optimality certificates at no added computational cost. Our results apply under nearly any stepsize selection and for a range of non-Lipschitz ill-conditioned problems where the early iterations of the subgradient method may diverge exponentially quickly (a phenomenon which, to the best of our knowledge, no prior works address). Even in the presence of such undesirable behaviors, our theory still ensures and bounds eventual convergence.

Gauges and Accelerated Optimization over Smooth and/or Strongly Convex Sets

We consider feasibility and constrained optimization problems defined over smooth and/or strongly convex sets. These notions mirror their popular function counterparts but are much less explored in the first-order optimization literature. We propose new scalable, projection-free, accelerated first-order methods in these settings. Our methods avoid linear optimization or projection oracles, only using cheap one-dimensional linesearches and normal vector computations. Despite this, we derive optimal accelerated convergence guarantees of $O(1/T)$ for strongly convex problems, $O(1/T^2)$ for smooth problems, and accelerated linear convergence given both. Our algorithms and analysis are based on novel characterizations of the Minkowski gauge of smooth and/or strongly convex sets, which may be of independent interest: although the gauge is neither smooth nor strongly convex, we show the gauge squared inherits any structure present in the set.

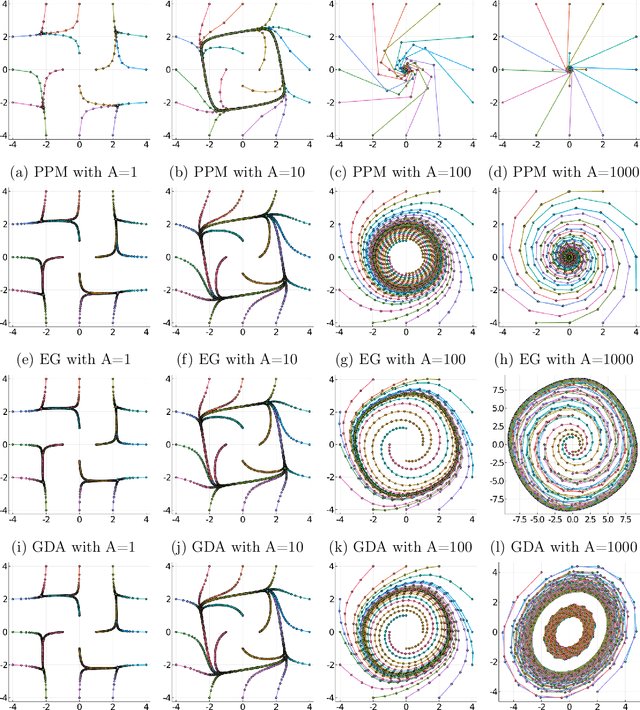
Limiting Behaviors of Nonconvex-Nonconcave Minimax Optimization via Continuous-Time Systems

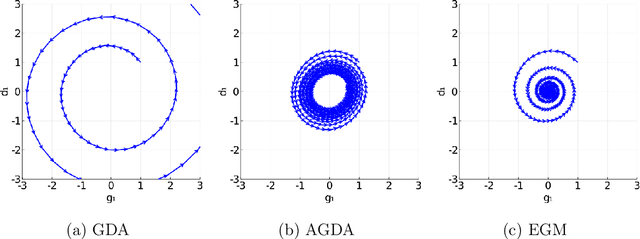
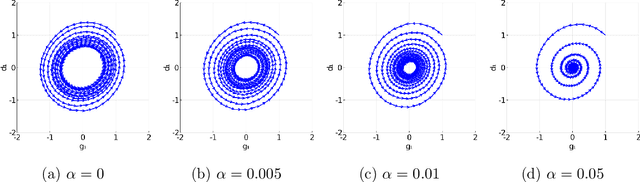
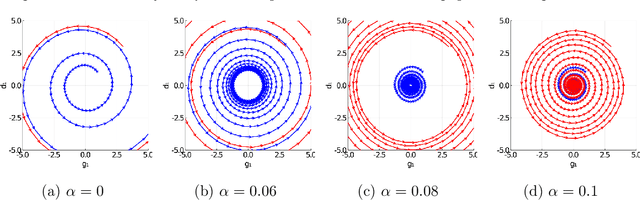
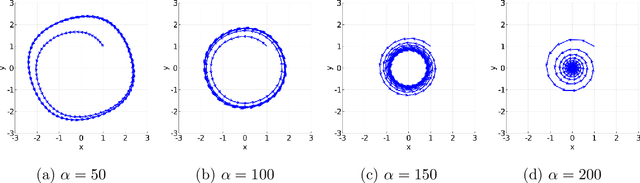
Unlike nonconvex optimization, where gradient descent is guaranteed to converge to a local optimizer, algorithms for nonconvex-nonconcave minimax optimization can have topologically different solution paths: sometimes converging to a solution, sometimes never converging and instead following a limit cycle, and sometimes diverging. In this paper, we study the limiting behaviors of three classic minimax algorithms: gradient decent ascent (GDA), alternating gradient decent ascent (AGDA), and the extragradient method (EGM). Numerically, we observe that all of these limiting behaviors can arise in Generative Adversarial Networks (GAN) training. To explain these different behaviors, we study the high-order resolution continuous-time dynamics that correspond to each algorithm, which results in the sufficient (and almost necessary) conditions for the local convergence by each method. Moreover, this ODE perspective allows us to characterize the phase transition between these different limiting behaviors caused by introducing regularization in the problem instance.

The Landscape of Nonconvex-Nonconcave Minimax Optimization

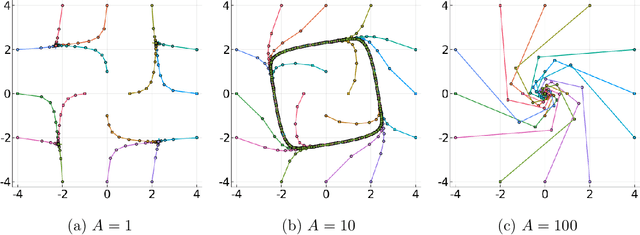
Minimax optimization has become a central tool for modern machine learning with applications in robust optimization, game theory and training GANs. These applications are often nonconvex-nonconcave, but the existing theory is unable to identify and deal with the fundamental difficulties posed by nonconvex-nonconcave structures. We break this historical barrier by identifying three regions of nonconvex-nonconcave bilinear minimax problems and characterizing their different solution paths. For problems where the interaction between the agents is sufficiently strong, we derive global linear convergence guarantees. Conversely when the interaction between the agents is fairly weak, we derive local linear convergence guarantees. Between these two settings, we show that limiting cycles may occur, preventing the convergence of the solution path.

Bundle Method Sketching for Low Rank Semidefinite Programming

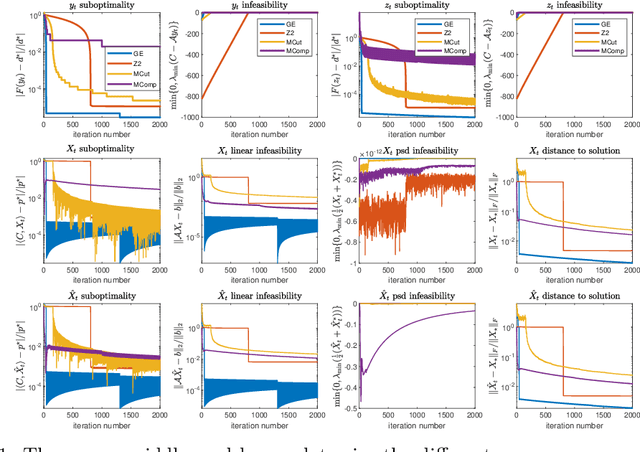
In this paper, we show that the bundle method can be applied to solve semidefinite programming problems with a low rank solution without ever constructing a full matrix. To accomplish this, we use recent results from randomly sketching matrix optimization problems and from the analysis of bundle methods. Under strong duality and strict complementarity of SDP, we achieve $\tilde{O}(\frac{1}{\epsilon})$ convergence rates for both the primal and the dual sequences, and the algorithm proposed outputs a $O(\sqrt{\epsilon})$ approximate solution $\hat{X}$ (measured by distances) with a low rank representation with at most $\tilde{O}(\frac{1}{\epsilon})$ many iterations.

Proximally Guided Stochastic Subgradient Method for Nonsmooth, Nonconvex Problems

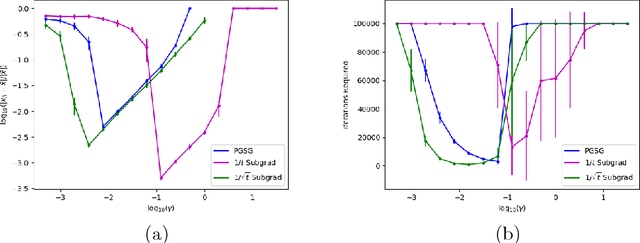
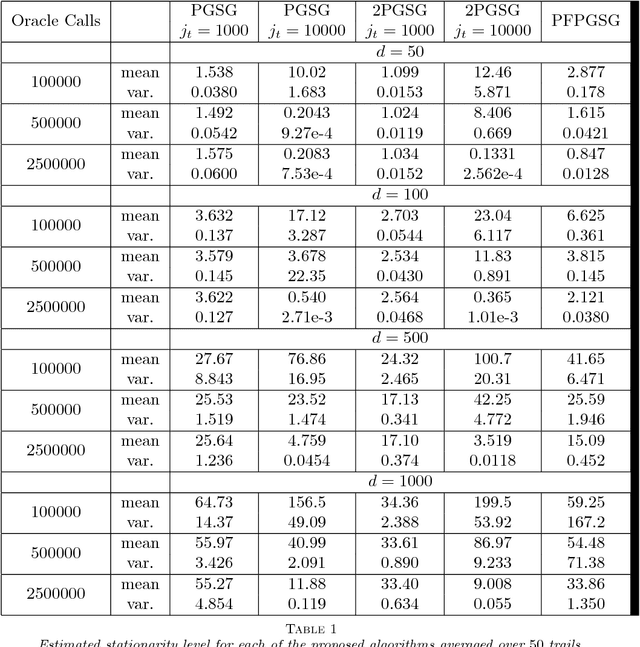
In this paper, we introduce a stochastic projected subgradient method for weakly convex (i.e., uniformly prox-regular) nonsmooth, nonconvex functions---a wide class of functions which includes the additive and convex composite classes. At a high-level, the method is an inexact proximal point iteration in which the strongly convex proximal subproblems are quickly solved with a specialized stochastic projected subgradient method. The primary contribution of this paper is a simple proof that the proposed algorithm converges at the same rate as the stochastic gradient method for smooth nonconvex problems. This result appears to be the first convergence rate analysis of a stochastic (or even deterministic) subgradient method for the class of weakly convex functions.

Convergence Rates for Deterministic and Stochastic Subgradient Methods Without Lipschitz Continuity

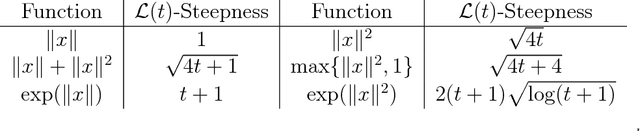
We extend the classic convergence rate theory for subgradient methods to apply to non-Lipschitz functions. For the deterministic projected subgradient method, we present a global $O(1/\sqrt{T})$ convergence rate for any convex function which is locally Lipschitz around its minimizers. This approach is based on Shor's classic subgradient analysis and implies generalizations of the standard convergence rates for gradient descent on functions with Lipschitz or H\"older continuous gradients. Further, we show a $O(1/\sqrt{T})$ convergence rate for the stochastic projected subgradient method on convex functions with at most quadratic growth, which improves to $O(1/T)$ under either strong convexity or a weaker quadratic lower bound condition.