Iteratively reweighted kernel machines efficiently learn sparse functions

The impressive practical performance of neural networks is often attributed to their ability to learn low-dimensional data representations and hierarchical structure directly from data. In this work, we argue that these two phenomena are not unique to neural networks, and can be elicited from classical kernel methods. Namely, we show that the derivative of the kernel predictor can detect the influential coordinates with low sample complexity. Moreover, by iteratively using the derivatives to reweight the data and retrain kernel machines, one is able to efficiently learn hierarchical polynomials with finite leap complexity. Numerical experiments illustrate the developed theory.

Online Covariance Estimation in Nonsmooth Stochastic Approximation

We consider applying stochastic approximation (SA) methods to solve nonsmooth variational inclusion problems. Existing studies have shown that the averaged iterates of SA methods exhibit asymptotic normality, with an optimal limiting covariance matrix in the local minimax sense of H\'ajek and Le Cam. However, no methods have been proposed to estimate this covariance matrix in a nonsmooth and potentially non-monotone (nonconvex) setting. In this paper, we study an online batch-means covariance matrix estimator introduced in Zhu et al.(2023). The estimator groups the SA iterates appropriately and computes the sample covariance among batches as an estimate of the limiting covariance. Its construction does not require prior knowledge of the total sample size, and updates can be performed recursively as new data arrives. We establish that, as long as the batch size sequence is properly specified (depending on the stepsize sequence), the estimator achieves a convergence rate of order $O(\sqrt{d}n^{-1/8+\varepsilon})$ for any $\varepsilon>0$, where $d$ and $n$ denote the problem dimensionality and the number of iterations (or samples) used. Although the problem is nonsmooth and potentially non-monotone (nonconvex), our convergence rate matches the best-known rate for covariance estimation methods using only first-order information in smooth and strongly-convex settings. The consistency of this covariance estimator enables asymptotically valid statistical inference, including constructing confidence intervals and performing hypothesis testing.

Gradient descent with adaptive stepsize converges (nearly) linearly under fourth-order growth

A prevalent belief among optimization specialists is that linear convergence of gradient descent is contingent on the function growing quadratically away from its minimizers. In this work, we argue that this belief is inaccurate. We show that gradient descent with an adaptive stepsize converges at a local (nearly) linear rate on any smooth function that merely exhibits fourth-order growth away from its minimizer. The adaptive stepsize we propose arises from an intriguing decomposition theorem: any such function admits a smooth manifold around the optimal solution -- which we call the ravine -- so that the function grows at least quadratically away from the ravine and has constant order growth along it. The ravine allows one to interlace many short gradient steps with a single long Polyak gradient step, which together ensure rapid convergence to the minimizer. We illustrate the theory and algorithm on the problems of matrix sensing and factorization and learning a single neuron in the overparameterized regime.

Aiming towards the minimizers: fast convergence of SGD for overparametrized problems

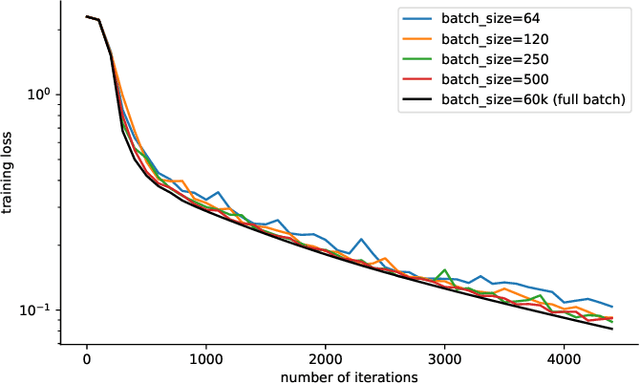
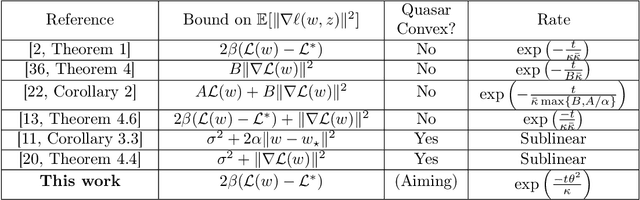
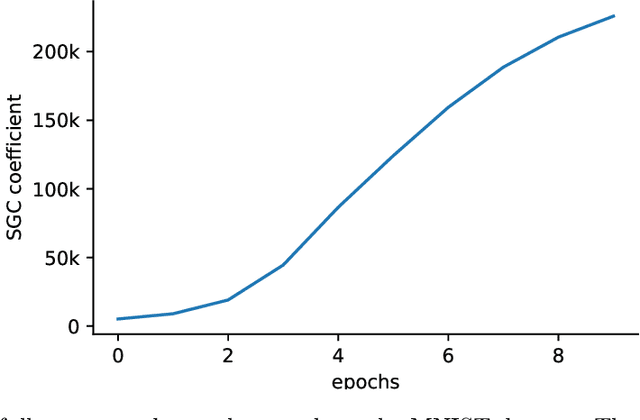
Modern machine learning paradigms, such as deep learning, occur in or close to the interpolation regime, wherein the number of model parameters is much larger than the number of data samples. In this work, we propose a regularity condition within the interpolation regime which endows the stochastic gradient method with the same worst-case iteration complexity as the deterministic gradient method, while using only a single sampled gradient (or a minibatch) in each iteration. In contrast, all existing guarantees require the stochastic gradient method to take small steps, thereby resulting in a much slower linear rate of convergence. Finally, we demonstrate that our condition holds when training sufficiently wide feedforward neural networks with a linear output layer.

Asymptotic normality and optimality in nonsmooth stochastic approximation

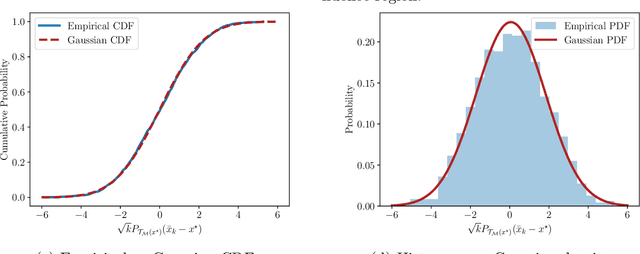
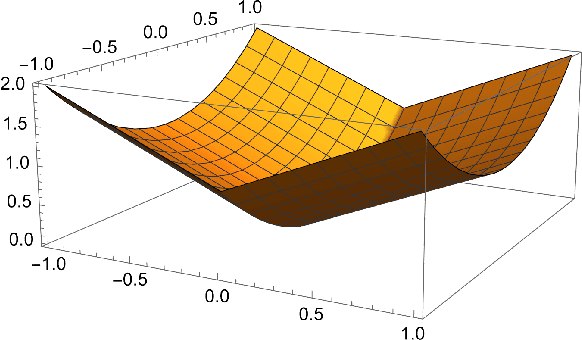
In their seminal work, Polyak and Juditsky showed that stochastic approximation algorithms for solving smooth equations enjoy a central limit theorem. Moreover, it has since been argued that the asymptotic covariance of the method is best possible among any estimation procedure in a local minimax sense of H\'{a}jek and Le Cam. A long-standing open question in this line of work is whether similar guarantees hold for important non-smooth problems, such as stochastic nonlinear programming or stochastic variational inequalities. In this work, we show that this is indeed the case.

Clustering a Mixture of Gaussians with Unknown Covariance

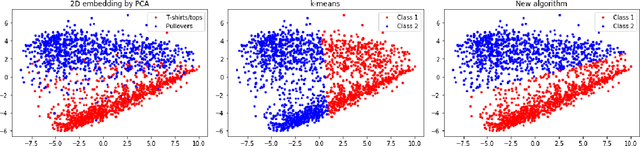
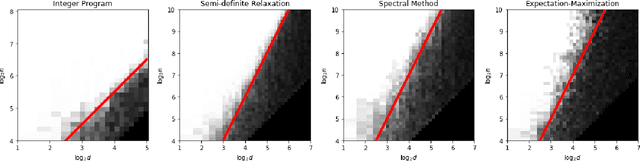
We investigate a clustering problem with data from a mixture of Gaussians that share a common but unknown, and potentially ill-conditioned, covariance matrix. We start by considering Gaussian mixtures with two equally-sized components and derive a Max-Cut integer program based on maximum likelihood estimation. We prove its solutions achieve the optimal misclassification rate when the number of samples grows linearly in the dimension, up to a logarithmic factor. However, solving the Max-cut problem appears to be computationally intractable. To overcome this, we develop an efficient spectral algorithm that attains the optimal rate but requires a quadratic sample size. Although this sample complexity is worse than that of the Max-cut problem, we conjecture that no polynomial-time method can perform better. Furthermore, we gather numerical and theoretical evidence that supports the existence of a statistical-computational gap. Finally, we generalize the Max-Cut program to a $k$-means program that handles multi-component mixtures with possibly unequal weights. It enjoys similar optimality guarantees for mixtures of distributions that satisfy a transportation-cost inequality, encompassing Gaussian and strongly log-concave distributions.

Subgradient methods near active manifolds: saddle point avoidance, local convergence, and asymptotic normality

Nonsmooth optimization problems arising in practice tend to exhibit beneficial smooth substructure: their domains stratify into "active manifolds" of smooth variation, which common proximal algorithms "identify" in finite time. Identification then entails a transition to smooth dynamics, and accommodates second-order acceleration techniques. While identification is clearly useful algorithmically, empirical evidence suggests that even those algorithms that do not identify the active manifold in finite time -- notably the subgradient method -- are nonetheless affected by it. This work seeks to explain this phenomenon, asking: how do active manifolds impact the subgradient method in nonsmooth optimization? In this work, we answer this question by introducing two algorithmically useful properties -- aiming and subgradient approximation -- that fully expose the smooth substructure of the problem. We show that these properties imply that the shadow of the (stochastic) subgradient method along the active manifold is precisely an inexact Riemannian gradient method with an implicit retraction. We prove that these properties hold for a wide class of problems, including cone reducible/decomposable functions and generic semialgebraic problems. Moreover, we develop a thorough calculus, proving such properties are preserved under smooth deformations and spectral lifts. This viewpoint then leads to several algorithmic consequences that parallel results in smooth optimization, despite the nonsmoothness of the problem: local rates of convergence, asymptotic normality, and saddle point avoidance. The asymptotic normality results appear to be new even in the most classical setting of stochastic nonlinear programming. The results culminate in the following observation: the perturbed subgradient method on generic, Clarke regular semialgebraic problems, converges only to local minimizers.

Escaping strict saddle points of the Moreau envelope in nonsmooth optimization

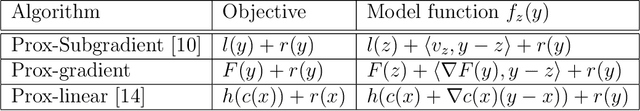
Recent work has shown that stochastically perturbed gradient methods can efficiently escape strict saddle points of smooth functions. We extend this body of work to nonsmooth optimization, by analyzing an inexact analogue of a stochastically perturbed gradient method applied to the Moreau envelope. The main conclusion is that a variety of algorithms for nonsmooth optimization can escape strict saddle points of the Moreau envelope at a controlled rate. The main technical insight is that typical algorithms applied to the proximal subproblem yield directions that approximate the gradient of the Moreau envelope in relative terms.

Active strict saddles in nonsmooth optimization

We introduce a geometrically transparent strict saddle property for nonsmooth functions. This property guarantees that simple proximal algorithms on weakly convex problems converge only to local minimizers, when randomly initialized. We argue that the strict saddle property may be a realistic assumption in applications, since it provably holds for generic semi-algebraic optimization problems.

Robust stochastic optimization with the proximal point method

Standard results in stochastic convex optimization bound the number of samples that an algorithm needs to generate a point with small function value in expectation. In this work, we show that a wide class of such algorithms on strongly convex problems can be augmented with high confidence bounds at an overhead cost that is only logarithmic in the confidence level and polylogarithmic in the condition number. We discuss consequences both for streaming and offline algorithms.