Chaoyue Liu
Hubs and Spokes Learning: Efficient and Scalable Collaborative Machine Learning
Apr 29, 2025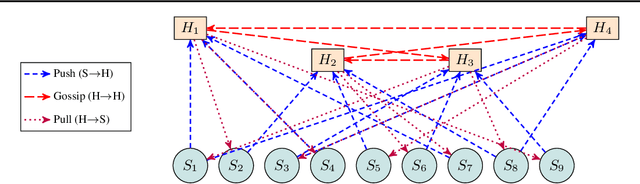
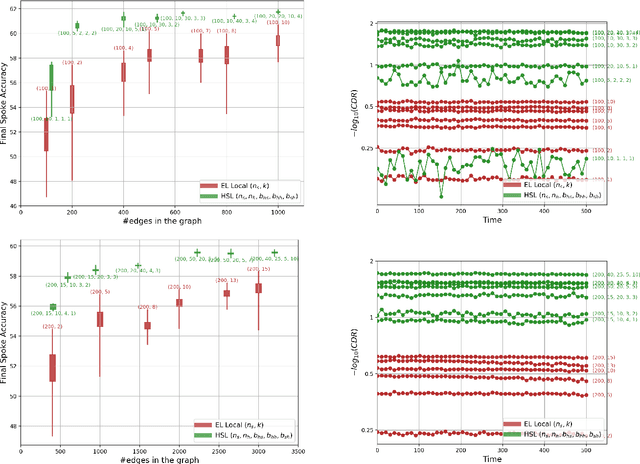
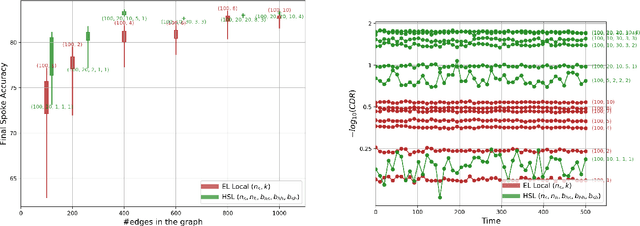
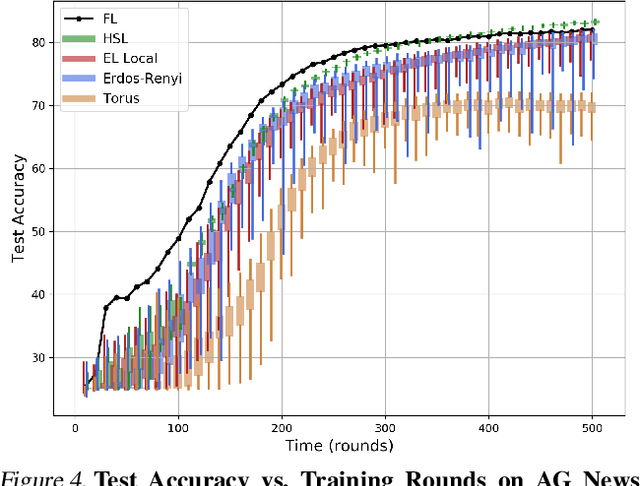
Abstract:We introduce the Hubs and Spokes Learning (HSL) framework, a novel paradigm for collaborative machine learning that combines the strengths of Federated Learning (FL) and Decentralized Learning (P2PL). HSL employs a two-tier communication structure that avoids the single point of failure inherent in FL and outperforms the state-of-the-art P2PL framework, Epidemic Learning Local (ELL). At equal communication budgets (total edges), HSL achieves higher performance than ELL, while at significantly lower communication budgets, it can match ELL's performance. For instance, with only 400 edges, HSL reaches the same test accuracy that ELL achieves with 1000 edges for 100 peers (spokes) on CIFAR-10, demonstrating its suitability for resource-constrained systems. HSL also achieves stronger consensus among nodes after mixing, resulting in improved performance with fewer training rounds. We substantiate these claims through rigorous theoretical analyses and extensive experimental results, showcasing HSL's practicality for large-scale collaborative learning.
DPZV: Resource Efficient ZO Optimization For Differentially Private VFL
Feb 27, 2025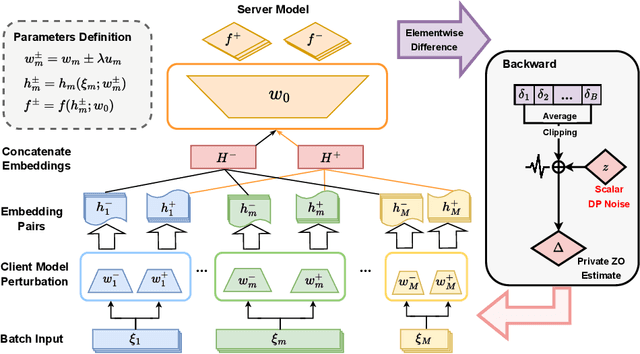

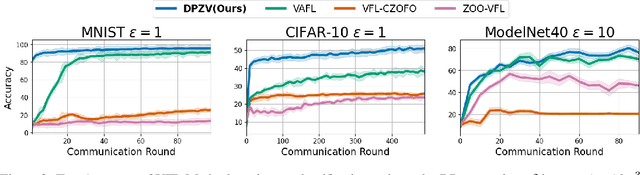
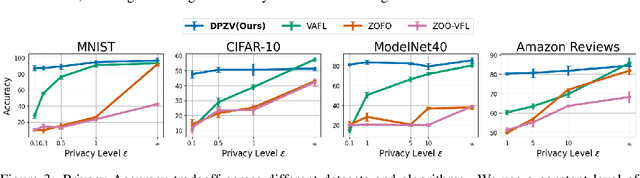
Abstract:Vertical Federated Learning (VFL) enables collaborative model training across feature-partitioned data, yet faces significant privacy risks and inefficiencies when scaling to large models. We propose DPZV, a memory-efficient Zeroth-Order(ZO) optimization framework that integrates differential privacy (DP) with vertical federated learning, addressing three critical challenges: (1) privacy vulnerabilities from gradient leakage, (2) high computation/communication costs of first-order methods, and (3) excessive memory footprint in conventional zeroth-order approaches. Our framework eliminates backpropagation through two-point gradient estimation, reducing client memory usage by 90\% compared to first-order counterparts while enabling asynchronous communication. By strategically injecting Gaussian noise on the server, DPZV achieves rigorous $(\epsilon, \delta)$-DP guarantees without third-party trust assumptions. Theoretical analysis establishes a convergence rate matching centralized case under non-convex objectives. Extensive experiments on image and NLP benchmarks demonstrate that DPZV outperforms all baselines in accuracy while providing strong privacy assurances ($\epsilon \leq 10$) and requiring far fewer computation resources, establishing new state-of-the-art privacy-utility tradeoffs for resource-constrained VFL deployments.
Parameter Tracking in Federated Learning with Adaptive Optimization
Feb 04, 2025



Abstract:In Federated Learning (FL), model training performance is strongly impacted by data heterogeneity across clients. Gradient Tracking (GT) has recently emerged as a solution which mitigates this issue by introducing correction terms to local model updates. To date, GT has only been considered under Stochastic Gradient Descent (SGD)-based model training, while modern FL frameworks increasingly employ adaptive optimizers for improved convergence. In this work, we generalize the GT framework to a more flexible Parameter Tracking (PT) paradigm and propose two novel adaptive optimization algorithms, {\tt FAdamET} and {\tt FAdamGT}, that integrate PT into Adam-based FL. We provide a rigorous convergence analysis of these algorithms under non-convex settings. Our experimental results demonstrate that both proposed algorithms consistently outperform existing methods when evaluating total communication cost and total computation cost across varying levels of data heterogeneity, showing the effectiveness of correcting first-order information in federated adaptive optimization.
Toward High-Performance Energy and Power Battery Cells with Machine Learning-based Optimization of Electrode Manufacturing
Jul 07, 2023Abstract:The optimization of the electrode manufacturing process is important for upscaling the application of Lithium Ion Batteries (LIBs) to cater for growing energy demand. In particular, LIB manufacturing is very important to be optimized because it determines the practical performance of the cells when the latter are being used in applications such as electric vehicles. In this study, we tackled the issue of high-performance electrodes for desired battery application conditions by proposing a powerful data-driven approach supported by a deterministic machine learning (ML)-assisted pipeline for bi-objective optimization of the electrochemical performance. This ML pipeline allows the inverse design of the process parameters to adopt in order to manufacture electrodes for energy or power applications. The latter work is an analogy to our previous work that supported the optimization of the electrode microstructures for kinetic, ionic, and electronic transport properties improvement. An electrochemical pseudo-two-dimensional model is fed with the electrode properties characterizing the electrode microstructures generated by manufacturing simulations and used to simulate the electrochemical performances. Secondly, the resulting dataset was used to train a deterministic ML model to implement fast bi-objective optimizations to identify optimal electrodes. Our results suggested a high amount of active material, combined with intermediate values of solid content in the slurry and calendering degree, to achieve the optimal electrodes.
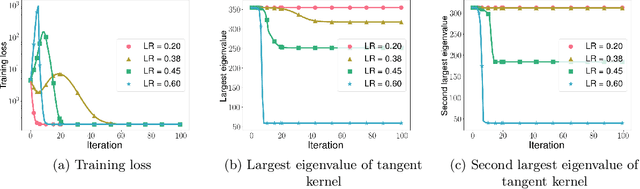
Catapults in SGD: spikes in the training loss and their impact on generalization through feature learning
Jun 07, 2023Abstract:In this paper, we first present an explanation regarding the common occurrence of spikes in the training loss when neural networks are trained with stochastic gradient descent (SGD). We provide evidence that the spikes in the training loss of SGD are "catapults", an optimization phenomenon originally observed in GD with large learning rates in [Lewkowycz et al. 2020]. We empirically show that these catapults occur in a low-dimensional subspace spanned by the top eigenvectors of the tangent kernel, for both GD and SGD. Second, we posit an explanation for how catapults lead to better generalization by demonstrating that catapults promote feature learning by increasing alignment with the Average Gradient Outer Product (AGOP) of the true predictor. Furthermore, we demonstrate that a smaller batch size in SGD induces a larger number of catapults, thereby improving AGOP alignment and test performance.
Aiming towards the minimizers: fast convergence of SGD for overparametrized problems
Jun 05, 2023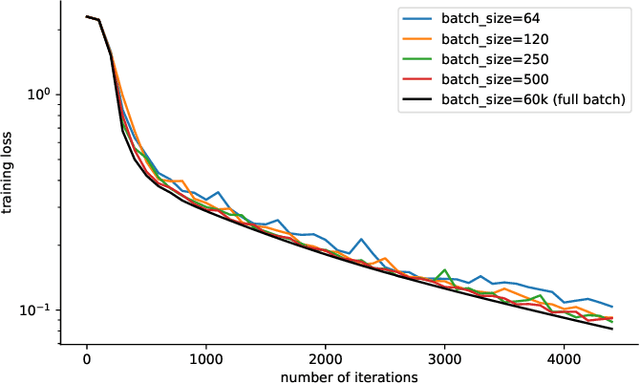
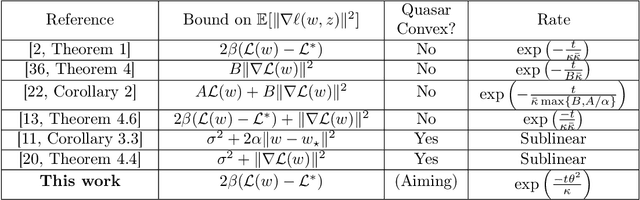
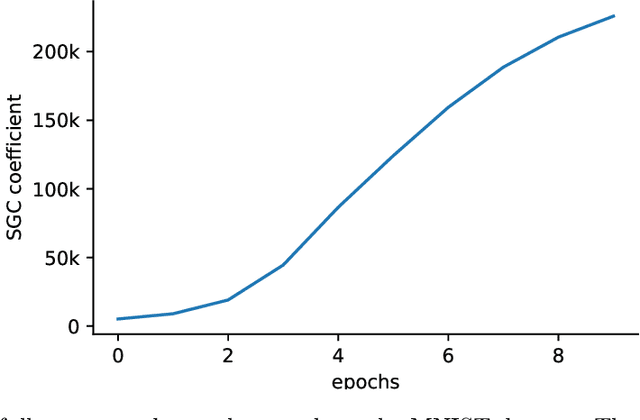
Abstract:Modern machine learning paradigms, such as deep learning, occur in or close to the interpolation regime, wherein the number of model parameters is much larger than the number of data samples. In this work, we propose a regularity condition within the interpolation regime which endows the stochastic gradient method with the same worst-case iteration complexity as the deterministic gradient method, while using only a single sampled gradient (or a minibatch) in each iteration. In contrast, all existing guarantees require the stochastic gradient method to take small steps, thereby resulting in a much slower linear rate of convergence. Finally, we demonstrate that our condition holds when training sufficiently wide feedforward neural networks with a linear output layer.
On Emergence of Clean-Priority Learning in Early Stopped Neural Networks
Jun 05, 2023



Abstract:When random label noise is added to a training dataset, the prediction error of a neural network on a label-noise-free test dataset initially improves during early training but eventually deteriorates, following a U-shaped dependence on training time. This behaviour is believed to be a result of neural networks learning the pattern of clean data first and fitting the noise later in the training, a phenomenon that we refer to as clean-priority learning. In this study, we aim to explore the learning dynamics underlying this phenomenon. We theoretically demonstrate that, in the early stage of training, the update direction of gradient descent is determined by the clean subset of training data, leaving the noisy subset has minimal to no impact, resulting in a prioritization of clean learning. Moreover, we show both theoretically and experimentally, as the clean-priority learning goes on, the dominance of the gradients of clean samples over those of noisy samples diminishes, and finally results in a termination of the clean-priority learning and fitting of the noisy samples.
ReLU soothes the NTK condition number and accelerates optimization for wide neural networks
May 15, 2023Abstract:Rectified linear unit (ReLU), as a non-linear activation function, is well known to improve the expressivity of neural networks such that any continuous function can be approximated to arbitrary precision by a sufficiently wide neural network. In this work, we present another interesting and important feature of ReLU activation function. We show that ReLU leads to: {\it better separation} for similar data, and {\it better conditioning} of neural tangent kernel (NTK), which are closely related. Comparing with linear neural networks, we show that a ReLU activated wide neural network at random initialization has a larger angle separation for similar data in the feature space of model gradient, and has a smaller condition number for NTK. Note that, for a linear neural network, the data separation and NTK condition number always remain the same as in the case of a linear model. Furthermore, we show that a deeper ReLU network (i.e., with more ReLU activation operations), has a smaller NTK condition number than a shallower one. Our results imply that ReLU activation, as well as the depth of ReLU network, helps improve the gradient descent convergence rate, which is closely related to the NTK condition number.
Quadratic models for understanding neural network dynamics
May 24, 2022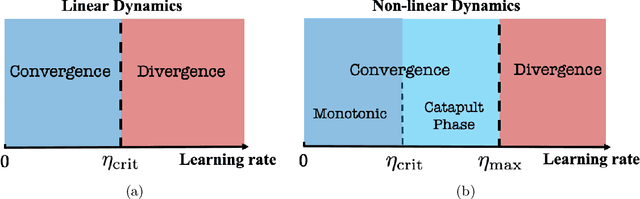
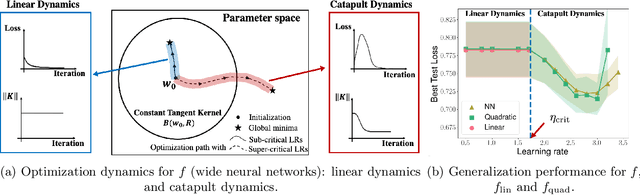
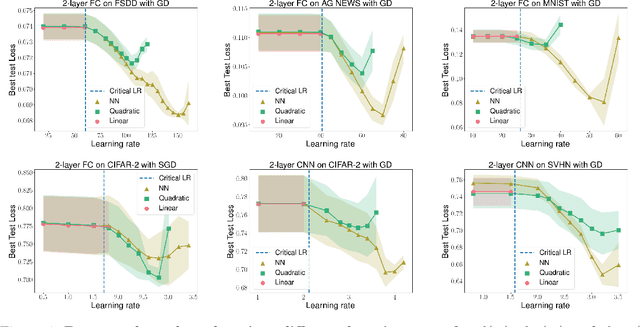
Abstract:In this work, we propose using a quadratic model as a tool for understanding properties of wide neural networks in both optimization and generalization. We show analytically that certain deep learning phenomena such as the "catapult phase" from [Lewkowycz et al. 2020], which cannot be captured by linear models, are manifested in the quadratic model for shallow ReLU networks. Furthermore, our empirical results indicate that the behaviour of quadratic models parallels that of neural networks in generalization, especially in the large learning rate regime. We expect that quadratic models will serve as a useful tool for analysis of neural networks.
Transition to Linearity of General Neural Networks with Directed Acyclic Graph Architecture
May 24, 2022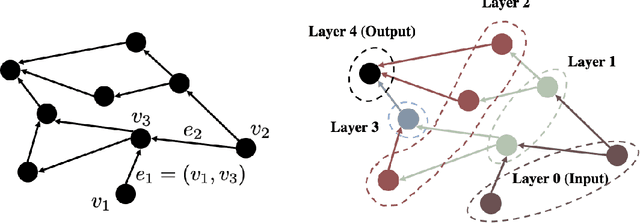
Abstract:In this paper we show that feedforward neural networks corresponding to arbitrary directed acyclic graphs undergo transition to linearity as their "width" approaches infinity. The width of these general networks is characterized by the minimum in-degree of their neurons, except for the input and first layers. Our results identify the mathematical structure underlying transition to linearity and generalize a number of recent works aimed at characterizing transition to linearity or constancy of the Neural Tangent Kernel for standard architectures.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge