Quadratic models for understanding neural network dynamics

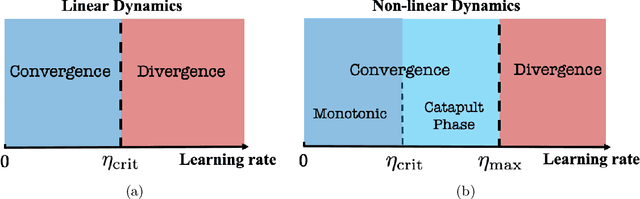
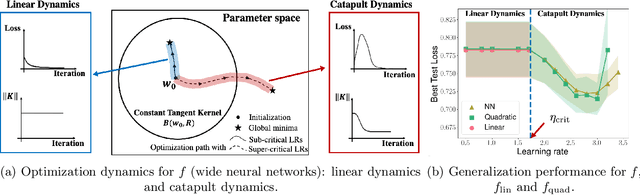
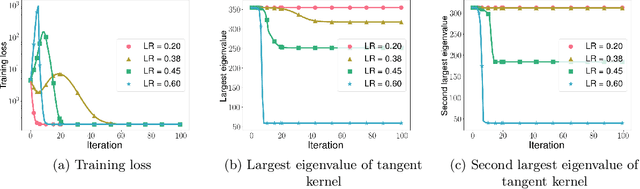
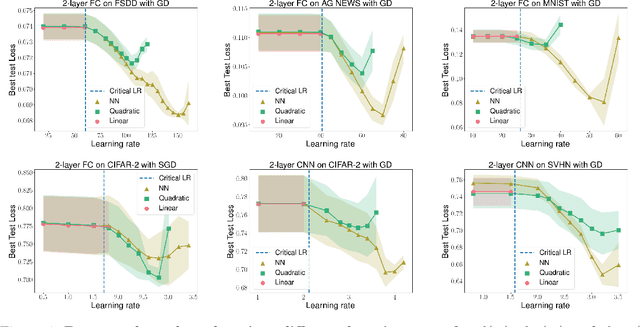
In this work, we propose using a quadratic model as a tool for understanding properties of wide neural networks in both optimization and generalization. We show analytically that certain deep learning phenomena such as the "catapult phase" from [Lewkowycz et al. 2020], which cannot be captured by linear models, are manifested in the quadratic model for shallow ReLU networks. Furthermore, our empirical results indicate that the behaviour of quadratic models parallels that of neural networks in generalization, especially in the large learning rate regime. We expect that quadratic models will serve as a useful tool for analysis of neural networks.