Aggregate and conquer: detecting and steering LLM concepts by combining nonlinear predictors over multiple layers

A trained Large Language Model (LLM) contains much of human knowledge. Yet, it is difficult to gauge the extent or accuracy of that knowledge, as LLMs do not always ``know what they know'' and may even be actively misleading. In this work, we give a general method for detecting semantic concepts in the internal activations of LLMs. Furthermore, we show that our methodology can be easily adapted to steer LLMs toward desirable outputs. Our innovations are the following: (1) we use a nonlinear feature learning method to identify important linear directions for predicting concepts from each layer; (2) we aggregate features across layers to build powerful concept detectors and steering mechanisms. We showcase the power of our approach by attaining state-of-the-art results for detecting hallucinations, harmfulness, toxicity, and untruthful content on seven benchmarks. We highlight the generality of our approach by steering LLMs towards new concepts that, to the best of our knowledge, have not been previously considered in the literature, including: semantic disambiguation, human languages, programming languages, hallucinated responses, science subjects, poetic/Shakespearean English, and even multiple concepts simultaneously. Moreover, our method can steer concepts with numerical attributes such as product reviews. We provide our code (including a simple API for our methods) at https://github.com/dmbeaglehole/neural_controllers .

Context-Scaling versus Task-Scaling in In-Context Learning

Transformers exhibit In-Context Learning (ICL), where these models solve new tasks by using examples in the prompt without additional training. In our work, we identify and analyze two key components of ICL: (1) context-scaling, where model performance improves as the number of in-context examples increases and (2) task-scaling, where model performance improves as the number of pre-training tasks increases. While transformers are capable of both context-scaling and task-scaling, we empirically show that standard Multi-Layer Perceptrons (MLPs) with vectorized input are only capable of task-scaling. To understand how transformers are capable of context-scaling, we first propose a significantly simplified transformer architecture without key, query, value weights. We show that it performs ICL comparably to the original GPT-2 model in various statistical learning tasks including linear regression, teacher-student settings. Furthermore, a single block of our simplified transformer can be viewed as data dependent feature map followed by an MLP. This feature map on its own is a powerful predictor that is capable of context-scaling but is not capable of task-scaling. We show empirically that concatenating the output of this feature map with vectorized data as an input to MLPs enables both context-scaling and task-scaling. This finding provides a simple setting to study context and task-scaling for ICL.

Emergence in non-neural models: grokking modular arithmetic via average gradient outer product

Neural networks trained to solve modular arithmetic tasks exhibit grokking, a phenomenon where the test accuracy starts improving long after the model achieves 100% training accuracy in the training process. It is often taken as an example of "emergence", where model ability manifests sharply through a phase transition. In this work, we show that the phenomenon of grokking is not specific to neural networks nor to gradient descent-based optimization. Specifically, we show that this phenomenon occurs when learning modular arithmetic with Recursive Feature Machines (RFM), an iterative algorithm that uses the Average Gradient Outer Product (AGOP) to enable task-specific feature learning with general machine learning models. When used in conjunction with kernel machines, iterating RFM results in a fast transition from random, near zero, test accuracy to perfect test accuracy. This transition cannot be predicted from the training loss, which is identically zero, nor from the test loss, which remains constant in initial iterations. Instead, as we show, the transition is completely determined by feature learning: RFM gradually learns block-circulant features to solve modular arithmetic. Paralleling the results for RFM, we show that neural networks that solve modular arithmetic also learn block-circulant features. Furthermore, we present theoretical evidence that RFM uses such block-circulant features to implement the Fourier Multiplication Algorithm, which prior work posited as the generalizing solution neural networks learn on these tasks. Our results demonstrate that emergence can result purely from learning task-relevant features and is not specific to neural architectures nor gradient descent-based optimization methods. Furthermore, our work provides more evidence for AGOP as a key mechanism for feature learning in neural networks.

Linear Recursive Feature Machines provably recover low-rank matrices

A fundamental problem in machine learning is to understand how neural networks make accurate predictions, while seemingly bypassing the curse of dimensionality. A possible explanation is that common training algorithms for neural networks implicitly perform dimensionality reduction - a process called feature learning. Recent work posited that the effects of feature learning can be elicited from a classical statistical estimator called the average gradient outer product (AGOP). The authors proposed Recursive Feature Machines (RFMs) as an algorithm that explicitly performs feature learning by alternating between (1) reweighting the feature vectors by the AGOP and (2) learning the prediction function in the transformed space. In this work, we develop the first theoretical guarantees for how RFM performs dimensionality reduction by focusing on the class of overparametrized problems arising in sparse linear regression and low-rank matrix recovery. Specifically, we show that RFM restricted to linear models (lin-RFM) generalizes the well-studied Iteratively Reweighted Least Squares (IRLS) algorithm. Our results shed light on the connection between feature learning in neural networks and classical sparse recovery algorithms. In addition, we provide an implementation of lin-RFM that scales to matrices with millions of missing entries. Our implementation is faster than the standard IRLS algorithm as it is SVD-free. It also outperforms deep linear networks for sparse linear regression and low-rank matrix completion.

Mechanism of feature learning in convolutional neural networks

Understanding the mechanism of how convolutional neural networks learn features from image data is a fundamental problem in machine learning and computer vision. In this work, we identify such a mechanism. We posit the Convolutional Neural Feature Ansatz, which states that covariances of filters in any convolutional layer are proportional to the average gradient outer product (AGOP) taken with respect to patches of the input to that layer. We present extensive empirical evidence for our ansatz, including identifying high correlation between covariances of filters and patch-based AGOPs for convolutional layers in standard neural architectures, such as AlexNet, VGG, and ResNets pre-trained on ImageNet. We also provide supporting theoretical evidence. We then demonstrate the generality of our result by using the patch-based AGOP to enable deep feature learning in convolutional kernel machines. We refer to the resulting algorithm as (Deep) ConvRFM and show that our algorithm recovers similar features to deep convolutional networks including the notable emergence of edge detectors. Moreover, we find that Deep ConvRFM overcomes previously identified limitations of convolutional kernels, such as their inability to adapt to local signals in images and, as a result, leads to sizable performance improvement over fixed convolutional kernels.

Catapults in SGD: spikes in the training loss and their impact on generalization through feature learning

In this paper, we first present an explanation regarding the common occurrence of spikes in the training loss when neural networks are trained with stochastic gradient descent (SGD). We provide evidence that the spikes in the training loss of SGD are "catapults", an optimization phenomenon originally observed in GD with large learning rates in [Lewkowycz et al. 2020]. We empirically show that these catapults occur in a low-dimensional subspace spanned by the top eigenvectors of the tangent kernel, for both GD and SGD. Second, we posit an explanation for how catapults lead to better generalization by demonstrating that catapults promote feature learning by increasing alignment with the Average Gradient Outer Product (AGOP) of the true predictor. Furthermore, we demonstrate that a smaller batch size in SGD induces a larger number of catapults, thereby improving AGOP alignment and test performance.

Feature learning in neural networks and kernel machines that recursively learn features

Neural networks have achieved impressive results on many technological and scientific tasks. Yet, their empirical successes have outpaced our fundamental understanding of their structure and function. By identifying mechanisms driving the successes of neural networks, we can provide principled approaches for improving neural network performance and develop simple and effective alternatives. In this work, we isolate the key mechanism driving feature learning in fully connected neural networks by connecting neural feature learning to the average gradient outer product. We subsequently leverage this mechanism to design \textit{Recursive Feature Machines} (RFMs), which are kernel machines that learn features. We show that RFMs (1) accurately capture features learned by deep fully connected neural networks, (2) close the gap between kernel machines and fully connected networks, and (3) surpass a broad spectrum of models including neural networks on tabular data. Furthermore, we demonstrate that RFMs shed light on recently observed deep learning phenomena such as grokking, lottery tickets, simplicity biases, and spurious features. We provide a Python implementation to make our method broadly accessible [\href{https://github.com/aradha/recursive_feature_machines}{GitHub}].

Transfer Learning with Kernel Methods

Transfer learning refers to the process of adapting a model trained on a source task to a target task. While kernel methods are conceptually and computationally simple machine learning models that are competitive on a variety of tasks, it has been unclear how to perform transfer learning for kernel methods. In this work, we propose a transfer learning framework for kernel methods by projecting and translating the source model to the target task. We demonstrate the effectiveness of our framework in applications to image classification and virtual drug screening. In particular, we show that transferring modern kernels trained on large-scale image datasets can result in substantial performance increase as compared to using the same kernel trained directly on the target task. In addition, we show that transfer-learned kernels allow a more accurate prediction of the effect of drugs on cancer cell lines. For both applications, we identify simple scaling laws that characterize the performance of transfer-learned kernels as a function of the number of target examples. We explain this phenomenon in a simplified linear setting, where we are able to derive the exact scaling laws. By providing a simple and effective transfer learning framework for kernel methods, our work enables kernel methods trained on large datasets to be easily adapted to a variety of downstream target tasks.

Quadratic models for understanding neural network dynamics

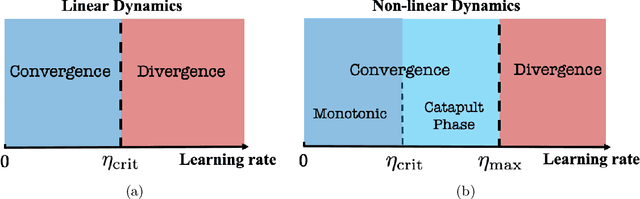
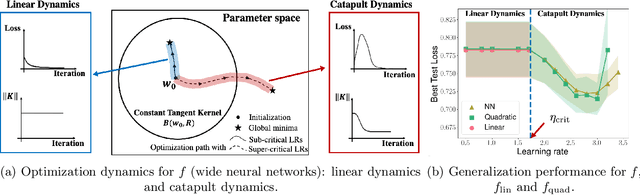
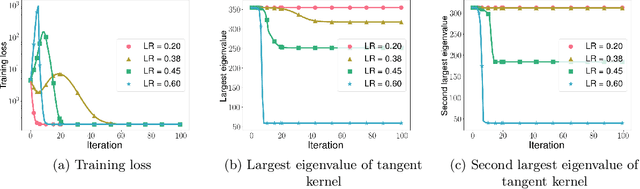
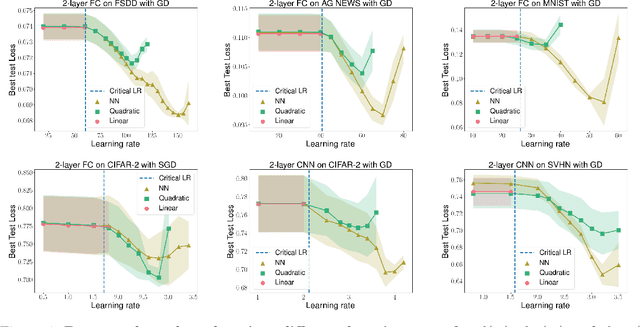
In this work, we propose using a quadratic model as a tool for understanding properties of wide neural networks in both optimization and generalization. We show analytically that certain deep learning phenomena such as the "catapult phase" from [Lewkowycz et al. 2020], which cannot be captured by linear models, are manifested in the quadratic model for shallow ReLU networks. Furthermore, our empirical results indicate that the behaviour of quadratic models parallels that of neural networks in generalization, especially in the large learning rate regime. We expect that quadratic models will serve as a useful tool for analysis of neural networks.

Wide and Deep Neural Networks Achieve Optimality for Classification

While neural networks are used for classification tasks across domains, a long-standing open problem in machine learning is determining whether neural networks trained using standard procedures are optimal for classification, i.e., whether such models minimize the probability of misclassification for arbitrary data distributions. In this work, we identify and construct an explicit set of neural network classifiers that achieve optimality. Since effective neural networks in practice are typically both wide and deep, we analyze infinitely wide networks that are also infinitely deep. In particular, using the recent connection between infinitely wide neural networks and Neural Tangent Kernels, we provide explicit activation functions that can be used to construct networks that achieve optimality. Interestingly, these activation functions are simple and easy to implement, yet differ from commonly used activations such as ReLU or sigmoid. More generally, we create a taxonomy of infinitely wide and deep networks and show that these models implement one of three well-known classifiers depending on the activation function used: (1) 1-nearest neighbor (model predictions are given by the label of the nearest training example); (2) majority vote (model predictions are given by the label of the class with greatest representation in the training set); or (3) singular kernel classifiers (a set of classifiers containing those that achieve optimality). Our results highlight the benefit of using deep networks for classification tasks, in contrast to regression tasks, where excessive depth is harmful.