Iteratively reweighted kernel machines efficiently learn sparse functions

The impressive practical performance of neural networks is often attributed to their ability to learn low-dimensional data representations and hierarchical structure directly from data. In this work, we argue that these two phenomena are not unique to neural networks, and can be elicited from classical kernel methods. Namely, we show that the derivative of the kernel predictor can detect the influential coordinates with low sample complexity. Moreover, by iteratively using the derivatives to reweight the data and retrain kernel machines, one is able to efficiently learn hierarchical polynomials with finite leap complexity. Numerical experiments illustrate the developed theory.

Online Covariance Estimation in Nonsmooth Stochastic Approximation

We consider applying stochastic approximation (SA) methods to solve nonsmooth variational inclusion problems. Existing studies have shown that the averaged iterates of SA methods exhibit asymptotic normality, with an optimal limiting covariance matrix in the local minimax sense of H\'ajek and Le Cam. However, no methods have been proposed to estimate this covariance matrix in a nonsmooth and potentially non-monotone (nonconvex) setting. In this paper, we study an online batch-means covariance matrix estimator introduced in Zhu et al.(2023). The estimator groups the SA iterates appropriately and computes the sample covariance among batches as an estimate of the limiting covariance. Its construction does not require prior knowledge of the total sample size, and updates can be performed recursively as new data arrives. We establish that, as long as the batch size sequence is properly specified (depending on the stepsize sequence), the estimator achieves a convergence rate of order $O(\sqrt{d}n^{-1/8+\varepsilon})$ for any $\varepsilon>0$, where $d$ and $n$ denote the problem dimensionality and the number of iterations (or samples) used. Although the problem is nonsmooth and potentially non-monotone (nonconvex), our convergence rate matches the best-known rate for covariance estimation methods using only first-order information in smooth and strongly-convex settings. The consistency of this covariance estimator enables asymptotically valid statistical inference, including constructing confidence intervals and performing hypothesis testing.

Invariant Kernels: Rank Stabilization and Generalization Across Dimensions

Symmetry arises often when learning from high dimensional data. For example, data sets consisting of point clouds, graphs, and unordered sets appear routinely in contemporary applications, and exhibit rich underlying symmetries. Understanding the benefits of symmetry on the statistical and numerical efficiency of learning algorithms is an active area of research. In this work, we show that symmetry has a pronounced impact on the rank of kernel matrices. Specifically, we compute the rank of a polynomial kernel of fixed degree that is invariant under various groups acting independently on its two arguments. In concrete circumstances, including the three aforementioned examples, symmetry dramatically decreases the rank making it independent of the data dimension. In such settings, we show that a simple regression procedure is minimax optimal for estimating an invariant polynomial from finitely many samples drawn across different dimensions. We complete the paper with numerical experiments that illustrate our findings.

Gradient descent with adaptive stepsize converges (nearly) linearly under fourth-order growth

A prevalent belief among optimization specialists is that linear convergence of gradient descent is contingent on the function growing quadratically away from its minimizers. In this work, we argue that this belief is inaccurate. We show that gradient descent with an adaptive stepsize converges at a local (nearly) linear rate on any smooth function that merely exhibits fourth-order growth away from its minimizer. The adaptive stepsize we propose arises from an intriguing decomposition theorem: any such function admits a smooth manifold around the optimal solution -- which we call the ravine -- so that the function grows at least quadratically away from the ravine and has constant order growth along it. The ravine allows one to interlace many short gradient steps with a single long Polyak gradient step, which together ensure rapid convergence to the minimizer. We illustrate the theory and algorithm on the problems of matrix sensing and factorization and learning a single neuron in the overparameterized regime.

The radius of statistical efficiency

Classical results in asymptotic statistics show that the Fisher information matrix controls the difficulty of estimating a statistical model from observed data. In this work, we introduce a companion measure of robustness of an estimation problem: the radius of statistical efficiency (RSE) is the size of the smallest perturbation to the problem data that renders the Fisher information matrix singular. We compute RSE up to numerical constants for a variety of test bed problems, including principal component analysis, generalized linear models, phase retrieval, bilinear sensing, and matrix completion. In all cases, the RSE quantifies the compatibility between the covariance of the population data and the latent model parameter. Interestingly, we observe a precise reciprocal relationship between RSE and the intrinsic complexity/sensitivity of the problem instance, paralleling the classical Eckart-Young theorem in numerical analysis.

Linear Recursive Feature Machines provably recover low-rank matrices

A fundamental problem in machine learning is to understand how neural networks make accurate predictions, while seemingly bypassing the curse of dimensionality. A possible explanation is that common training algorithms for neural networks implicitly perform dimensionality reduction - a process called feature learning. Recent work posited that the effects of feature learning can be elicited from a classical statistical estimator called the average gradient outer product (AGOP). The authors proposed Recursive Feature Machines (RFMs) as an algorithm that explicitly performs feature learning by alternating between (1) reweighting the feature vectors by the AGOP and (2) learning the prediction function in the transformed space. In this work, we develop the first theoretical guarantees for how RFM performs dimensionality reduction by focusing on the class of overparametrized problems arising in sparse linear regression and low-rank matrix recovery. Specifically, we show that RFM restricted to linear models (lin-RFM) generalizes the well-studied Iteratively Reweighted Least Squares (IRLS) algorithm. Our results shed light on the connection between feature learning in neural networks and classical sparse recovery algorithms. In addition, we provide an implementation of lin-RFM that scales to matrices with millions of missing entries. Our implementation is faster than the standard IRLS algorithm as it is SVD-free. It also outperforms deep linear networks for sparse linear regression and low-rank matrix completion.

Aiming towards the minimizers: fast convergence of SGD for overparametrized problems

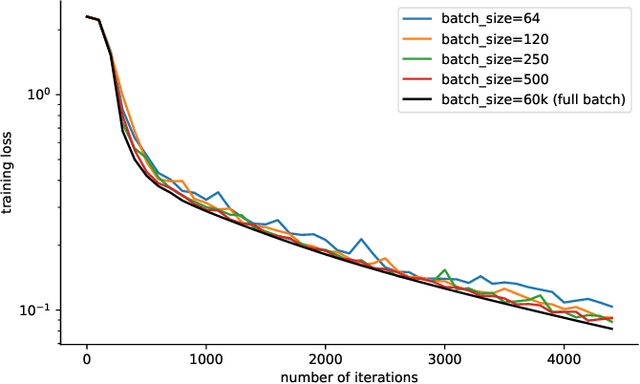
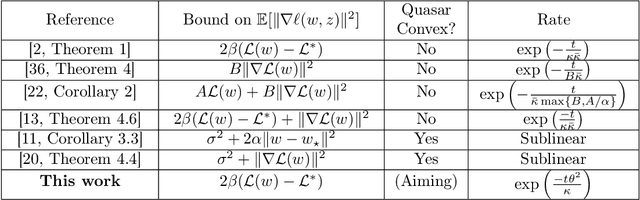
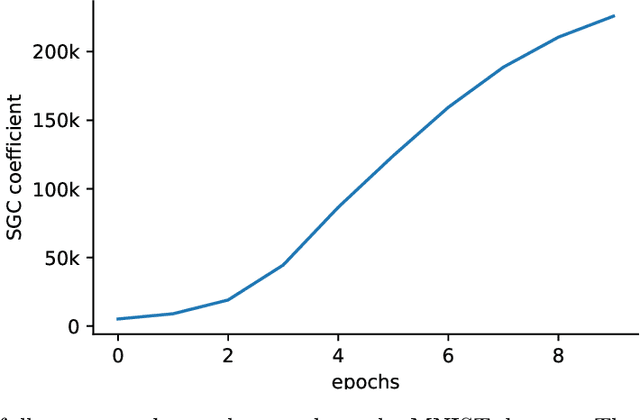
Modern machine learning paradigms, such as deep learning, occur in or close to the interpolation regime, wherein the number of model parameters is much larger than the number of data samples. In this work, we propose a regularity condition within the interpolation regime which endows the stochastic gradient method with the same worst-case iteration complexity as the deterministic gradient method, while using only a single sampled gradient (or a minibatch) in each iteration. In contrast, all existing guarantees require the stochastic gradient method to take small steps, thereby resulting in a much slower linear rate of convergence. Finally, we demonstrate that our condition holds when training sufficiently wide feedforward neural networks with a linear output layer.

Asymptotic normality and optimality in nonsmooth stochastic approximation

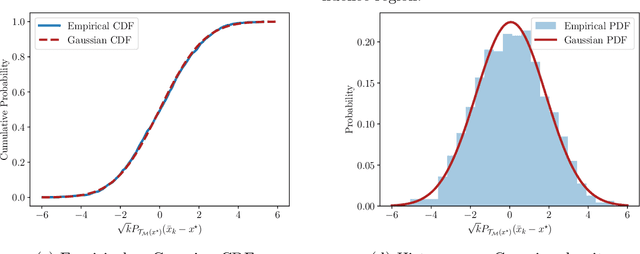
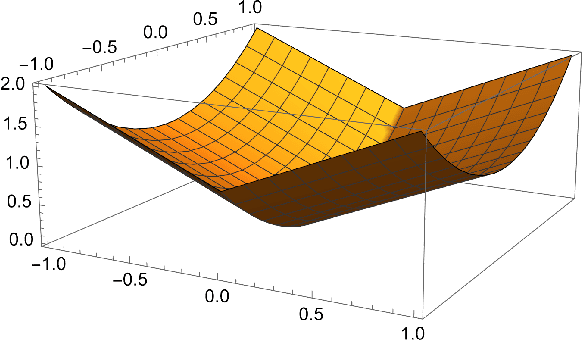
In their seminal work, Polyak and Juditsky showed that stochastic approximation algorithms for solving smooth equations enjoy a central limit theorem. Moreover, it has since been argued that the asymptotic covariance of the method is best possible among any estimation procedure in a local minimax sense of H\'{a}jek and Le Cam. A long-standing open question in this line of work is whether similar guarantees hold for important non-smooth problems, such as stochastic nonlinear programming or stochastic variational inequalities. In this work, we show that this is indeed the case.

Stochastic approximation with decision-dependent distributions: asymptotic normality and optimality

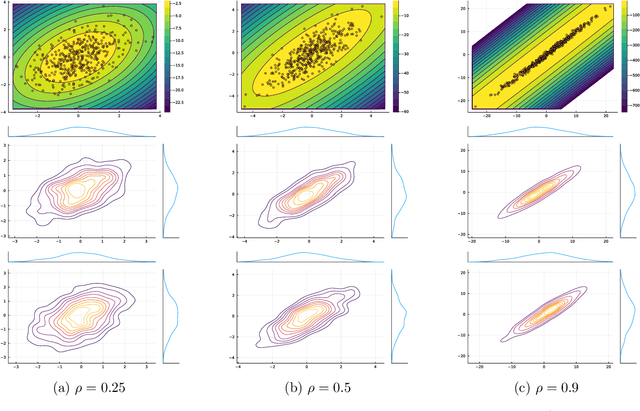
We analyze a stochastic approximation algorithm for decision-dependent problems, wherein the data distribution used by the algorithm evolves along the iterate sequence. The primary examples of such problems appear in performative prediction and its multiplayer extensions. We show that under mild assumptions, the deviation between the average iterate of the algorithm and the solution is asymptotically normal, with a covariance that nicely decouples the effects of the gradient noise and the distributional shift. Moreover, building on the work of H\'ajek and Le Cam, we show that the asymptotic performance of the algorithm is locally minimax optimal.

Decision-Dependent Risk Minimization in Geometrically Decaying Dynamic Environments

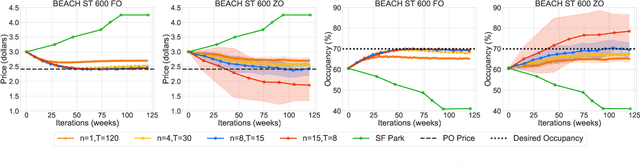
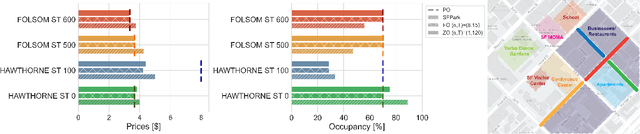
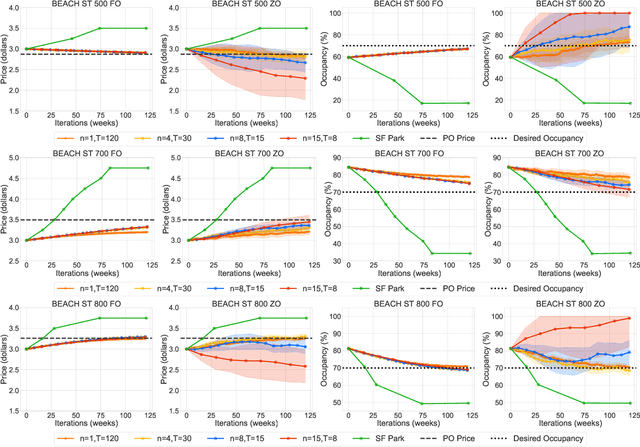
This paper studies the problem of expected loss minimization given a data distribution that is dependent on the decision-maker's action and evolves dynamically in time according to a geometric decay process. Novel algorithms for both the information setting in which the decision-maker has a first order gradient oracle and the setting in which they have simply a loss function oracle are introduced. The algorithms operate on the same underlying principle: the decision-maker repeatedly deploys a fixed decision over the length of an epoch, thereby allowing the dynamically changing environment to sufficiently mix before updating the decision. The iteration complexity in each of the settings is shown to match existing rates for first and zero order stochastic gradient methods up to logarithmic factors. The algorithms are evaluated on a "semi-synthetic" example using real world data from the SFpark dynamic pricing pilot study; it is shown that the announced prices result in an improvement for the institution's objective (target occupancy), while achieving an overall reduction in parking rates.