Decision-Dependent Risk Minimization in Geometrically Decaying Dynamic Environments

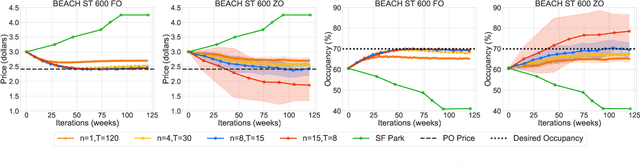
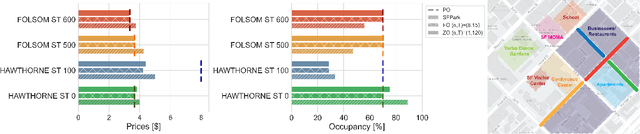
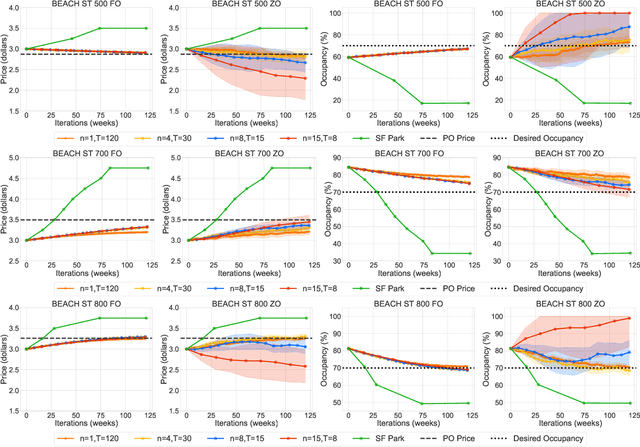
This paper studies the problem of expected loss minimization given a data distribution that is dependent on the decision-maker's action and evolves dynamically in time according to a geometric decay process. Novel algorithms for both the information setting in which the decision-maker has a first order gradient oracle and the setting in which they have simply a loss function oracle are introduced. The algorithms operate on the same underlying principle: the decision-maker repeatedly deploys a fixed decision over the length of an epoch, thereby allowing the dynamically changing environment to sufficiently mix before updating the decision. The iteration complexity in each of the settings is shown to match existing rates for first and zero order stochastic gradient methods up to logarithmic factors. The algorithms are evaluated on a "semi-synthetic" example using real world data from the SFpark dynamic pricing pilot study; it is shown that the announced prices result in an improvement for the institution's objective (target occupancy), while achieving an overall reduction in parking rates.

Function Design for Improved Competitive Ratio in Online Resource Allocation with Procurement Costs

We study the problem of online resource allocation, where multiple customers arrive sequentially and the seller must irrevocably allocate resources to each incoming customer while also facing a procurement cost for the total allocation. Assuming resource procurement follows an a priori known marginally increasing cost function, the objective is to maximize the reward obtained from fulfilling the customers' requests sans the cumulative procurement cost. We analyze the competitive ratio of a primal-dual algorithm in this setting, and develop an optimization framework for synthesizing a surrogate function for the procurement cost function to be used by the algorithm, in order to improve the competitive ratio of the primal-dual algorithm. Our first design method focuses on polynomial procurement cost functions and uses the optimal surrogate function to provide a more refined bound than the state of the art. Our second design method uses quasiconvex optimization to find optimal design parameters for a general class of procurement cost functions. Numerical examples are used to illustrate the design techniques. We conclude by extending the analysis to devise a posted pricing mechanism in which the algorithm does not require the customers' preferences to be revealed.

Best of many worlds: Robust model selection for online supervised learning

We introduce algorithms for online, full-information prediction that are competitive with contextual tree experts of unknown complexity, in both probabilistic and adversarial settings. We show that by incorporating a probabilistic framework of structural risk minimization into existing adaptive algorithms, we can robustly learn not only the presence of stochastic structure when it exists (leading to constant as opposed to $\mathcal{O}(\sqrt{T})$ regret), but also the correct model order. We thus obtain regret bounds that are competitive with the regret of an optimal algorithm that possesses strong side information about both the complexity of the optimal contextual tree expert and whether the process generating the data is stochastic or adversarial. These are the first constructive guarantees on simultaneous adaptivity to the model and the presence of stochasticity.