Learning to Incentivize in Repeated Principal-Agent Problems with Adversarial Agent Arrivals

We initiate the study of a repeated principal-agent problem over a finite horizon $T$, where a principal sequentially interacts with $K\geq 2$ types of agents arriving in an adversarial order. At each round, the principal strategically chooses one of the $N$ arms to incentivize for an arriving agent of unknown type. The agent then chooses an arm based on its own utility and the provided incentive, and the principal receives a corresponding reward. The objective is to minimize regret against the best incentive in hindsight. Without prior knowledge of agent behavior, we show that the problem becomes intractable, leading to linear regret. We analyze two key settings where sublinear regret is achievable. In the first setting, the principal knows the arm each agent type would select greedily for any given incentive. Under this setting, we propose an algorithm that achieves a regret bound of $O(\min\{\sqrt{KT\log N},K\sqrt{T}\})$ and provide a matching lower bound up to a $\log K$ factor. In the second setting, an agent's response varies smoothly with the incentive and is governed by a Lipschitz constant $L\geq 1$. Under this setting, we show that there is an algorithm with a regret bound of $\tilde{O}((LN)^{1/3}T^{2/3})$ and establish a matching lower bound up to logarithmic factors. Finally, we extend our algorithmic results for both settings by allowing the principal to incentivize multiple arms simultaneously in each round.

Improved Regret and Contextual Linear Extension for Pandora's Box and Prophet Inequality

We study the Pandora's Box problem in an online learning setting with semi-bandit feedback. In each round, the learner sequentially pays to open up to $n$ boxes with unknown reward distributions, observes rewards upon opening, and decides when to stop. The utility of the learner is the maximum observed reward minus the cumulative cost of opened boxes, and the goal is to minimize regret defined as the gap between the cumulative expected utility and that of the optimal policy. We propose a new algorithm that achieves $\widetilde{O}(\sqrt{nT})$ regret after $T$ rounds, which improves the $\widetilde{O}(n\sqrt{T})$ bound of Agarwal et al. [2024] and matches the known lower bound up to logarithmic factors. To better capture real-life applications, we then extend our results to a natural but challenging contextual linear setting, where each box's expected reward is linear in some known but time-varying $d$-dimensional context and the noise distribution is fixed over time. We design an algorithm that learns both the linear function and the noise distributions, achieving $\widetilde{O}(nd\sqrt{T})$ regret. Finally, we show that our techniques also apply to the online Prophet Inequality problem, where the learner must decide immediately whether or not to accept a revealed reward. In both non-contextual and contextual settings, our approach achieves similar improvements and regret bounds.

Efficient Near-Optimal Algorithm for Online Shortest Paths in Directed Acyclic Graphs with Bandit Feedback Against Adaptive Adversaries

In this paper, we study the online shortest path problem in directed acyclic graphs (DAGs) under bandit feedback against an adaptive adversary. Given a DAG $G = (V, E)$ with a source node $v_{\mathsf{s}}$ and a sink node $v_{\mathsf{t}}$, let $X \subseteq \{0,1\}^{|E|}$ denote the set of all paths from $v_{\mathsf{s}}$ to $v_{\mathsf{t}}$. At each round $t$, we select a path $\mathbf{x}_t \in X$ and receive bandit feedback on our loss $\langle \mathbf{x}_t, \mathbf{y}_t \rangle \in [-1,1]$, where $\mathbf{y}_t$ is an adversarially chosen loss vector. Our goal is to minimize regret with respect to the best path in hindsight over $T$ rounds. We propose the first computationally efficient algorithm to achieve a near-minimax optimal regret bound of $\tilde O(\sqrt{|E|T\log |X|})$ with high probability against any adaptive adversary, where $\tilde O(\cdot)$ hides logarithmic factors in the number of edges $|E|$. Our algorithm leverages a novel loss estimator and a centroid-based decomposition in a nontrivial manner to attain this regret bound. As an application, we show that our algorithm for DAGs provides state-of-the-art efficient algorithms for $m$-sets, extensive-form games, the Colonel Blotto game, shortest walks in directed graphs, hypercubes, and multi-task multi-armed bandits, achieving improved high-probability regret guarantees in all these settings.

S4S: Solving for a Diffusion Model Solver

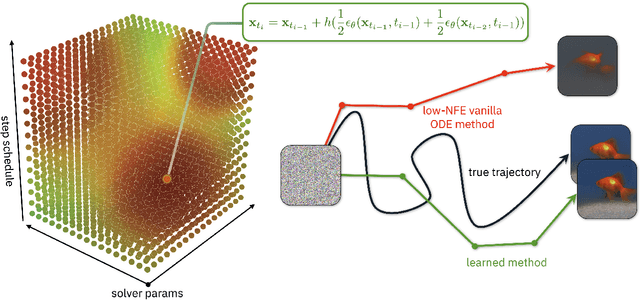
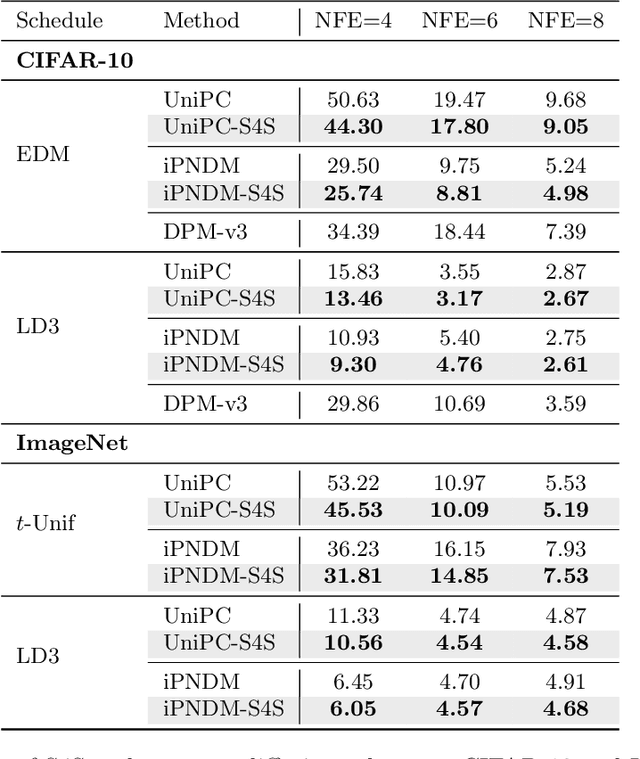
Diffusion models (DMs) create samples from a data distribution by starting from random noise and iteratively solving a reverse-time ordinary differential equation (ODE). Because each step in the iterative solution requires an expensive neural function evaluation (NFE), there has been significant interest in approximately solving these diffusion ODEs with only a few NFEs without modifying the underlying model. However, in the few NFE regime, we observe that tracking the true ODE evolution is fundamentally impossible using traditional ODE solvers. In this work, we propose a new method that learns a good solver for the DM, which we call Solving for the Solver (S4S). S4S directly optimizes a solver to obtain good generation quality by learning to match the output of a strong teacher solver. We evaluate S4S on six different pre-trained DMs, including pixel-space and latent-space DMs for both conditional and unconditional sampling. In all settings, S4S uniformly improves the sample quality relative to traditional ODE solvers. Moreover, our method is lightweight, data-free, and can be plugged in black-box on top of any discretization schedule or architecture to improve performance. Building on top of this, we also propose S4S-Alt, which optimizes both the solver and the discretization schedule. By exploiting the full design space of DM solvers, with 5 NFEs, we achieve an FID of 3.73 on CIFAR10 and 13.26 on MS-COCO, representing a $1.5\times$ improvement over previous training-free ODE methods.

A Learning Algorithm That Attains the Human Optimum in a Repeated Human-Machine Interaction Game

When humans interact with learning-based control systems, a common goal is to minimize a cost function known only to the human. For instance, an exoskeleton may adapt its assistance in an effort to minimize the human's metabolic cost-of-transport. Conventional approaches to synthesizing the learning algorithm solve an inverse problem to infer the human's cost. However, these problems can be ill-posed, hard to solve, or sensitive to problem data. Here we show a game-theoretic learning algorithm that works solely by observing human actions to find the cost minimum, avoiding the need to solve an inverse problem. We evaluate the performance of our algorithm in an extensive set of human subjects experiments, demonstrating consistent convergence to the minimum of a prescribed human cost function in scalar and multidimensional instantiations of the game. We conclude by outlining future directions for theoretical and empirical extensions of our results.

Principal-Agent Bandit Games with Self-Interested and Exploratory Learning Agents

We study the repeated principal-agent bandit game, where the principal indirectly interacts with the unknown environment by proposing incentives for the agent to play arms. Most existing work assumes the agent has full knowledge of the reward means and always behaves greedily, but in many online marketplaces, the agent needs to learn the unknown environment and sometimes explore. Motivated by such settings, we model a self-interested learning agent with exploration behaviors who iteratively updates reward estimates and either selects an arm that maximizes the estimated reward plus incentive or explores arbitrarily with a certain probability. As a warm-up, we first consider a self-interested learning agent without exploration. We propose algorithms for both i.i.d. and linear reward settings with bandit feedback in a finite horizon $T$, achieving regret bounds of $\widetilde{O}(\sqrt{T})$ and $\widetilde{O}( T^{2/3} )$, respectively. Specifically, these algorithms are established upon a novel elimination framework coupled with newly-developed search algorithms which accommodate the uncertainty arising from the learning behavior of the agent. We then extend the framework to handle the exploratory learning agent and develop an algorithm to achieve a $\widetilde{O}(T^{2/3})$ regret bound in i.i.d. reward setup by enhancing the robustness of our elimination framework to the potential agent exploration. Finally, when reducing our agent behaviors to the one studied in (Dogan et al., 2023a), we propose an algorithm based on our robust framework, which achieves a $\widetilde{O}(\sqrt{T})$ regret bound, significantly improving upon their $\widetilde{O}(T^{11/12})$ bound.

Effect of Adaptation Rate and Cost Display in a Human-AI Interaction Game

As interactions between humans and AI become more prevalent, it is critical to have better predictors of human behavior in these interactions. We investigated how changes in the AI's adaptive algorithm impact behavior predictions in two-player continuous games. In our experiments, the AI adapted its actions using a gradient descent algorithm under different adaptation rates while human participants were provided cost feedback. The cost feedback was provided by one of two types of visual displays: (a) cost at the current joint action vector, or (b) cost in a local neighborhood of the current joint action vector. Our results demonstrate that AI adaptation rate can significantly affect human behavior, having the ability to shift the outcome between two game theoretic equilibrium. We observed that slow adaptation rates shift the outcome towards the Nash equilibrium, while fast rates shift the outcome towards the human-led Stackelberg equilibrium. The addition of localized cost information had the effect of shifting outcomes towards Nash, compared to the outcomes from cost information at only the current joint action vector. Future work will investigate other effects that influence the convergence of gradient descent games.

Initializing Services in Interactive ML Systems for Diverse Users

This paper studies ML systems that interactively learn from users across multiple subpopulations with heterogeneous data distributions. The primary objective is to provide specialized services for different user groups while also predicting user preferences. Once the users select a service based on how well the service anticipated their preference, the services subsequently adapt and refine themselves based on the user data they accumulate, resulting in an iterative, alternating minimization process between users and services (learning dynamics). Employing such tailored approaches has two main challenges: (i) Unknown user preferences: Typically, data on user preferences are unavailable without interaction, and uniform data collection across a large and diverse user base can be prohibitively expensive. (ii) Suboptimal Local Solutions: The total loss (sum of loss functions across all users and all services) landscape is not convex even if the individual losses on a single service are convex, making it likely for the learning dynamics to get stuck in local minima. The final outcome of the aforementioned learning dynamics is thus strongly influenced by the initial set of services offered to users, and is not guaranteed to be close to the globally optimal outcome. In this work, we propose a randomized algorithm to adaptively select very few users to collect preference data from, while simultaneously initializing a set of services. We prove that under mild assumptions on the loss functions, the expected total loss achieved by the algorithm right after initialization is within a factor of the globally optimal total loss with complete user preference data, and this factor scales only logarithmically in the number of services. Our theory is complemented by experiments on real as well as semi-synthetic datasets.

Near-Optimal Pure Exploration in Matrix Games: A Generalization of Stochastic Bandits & Dueling Bandits

We study the sample complexity of identifying the pure strategy Nash equilibrium (PSNE) in a two-player zero-sum matrix game with noise. Formally, we are given a stochastic model where any learner can sample an entry $(i,j)$ of the input matrix $A\in[-1,1]^{n\times m}$ and observe $A_{i,j}+\eta$ where $\eta$ is a zero-mean 1-sub-Gaussian noise. The aim of the learner is to identify the PSNE of $A$, whenever it exists, with high probability while taking as few samples as possible. Zhou et al. (2017) presents an instance-dependent sample complexity lower bound that depends only on the entries in the row and column in which the PSNE lies. We design a near-optimal algorithm whose sample complexity matches the lower bound, up to log factors. The problem of identifying the PSNE also generalizes the problem of pure exploration in stochastic multi-armed bandits and dueling bandits, and our result matches the optimal bounds, up to log factors, in both the settings.

Logarithmic Regret for Matrix Games against an Adversary with Noisy Bandit Feedback

This paper considers a variant of zero-sum matrix games where at each timestep the row player chooses row $i$, the column player chooses column $j$, and the row player receives a noisy reward with mean $A_{i,j}$. The objective of the row player is to accumulate as much reward as possible, even against an adversarial column player. If the row player uses the EXP3 strategy, an algorithm known for obtaining $\sqrt{T}$ regret against an arbitrary sequence of rewards, it is immediate that the row player also achieves $\sqrt{T}$ regret relative to the Nash equilibrium in this game setting. However, partly motivated by the fact that the EXP3 strategy is myopic to the structure of the game, O'Donoghue et al. (2021) proposed a UCB-style algorithm that leverages the game structure and demonstrated that this algorithm greatly outperforms EXP3 empirically. While they showed that this UCB-style algorithm achieved $\sqrt{T}$ regret, in this paper we ask if there exists an algorithm that provably achieves $\text{polylog}(T)$ regret against any adversary, analogous to results from stochastic bandits. We propose a novel algorithm that answers this question in the affirmative for the simple $2 \times 2$ setting, providing the first instance-dependent guarantees for games in the regret setting. Our algorithm overcomes two major hurdles: 1) obtaining logarithmic regret even though the Nash equilibrium is estimable only at a $1/\sqrt{T}$ rate, and 2) designing row-player strategies that guarantee that either the adversary provides information about the Nash equilibrium, or the row player incurs negative regret. Moreover, in the full information case we address the general $n \times m$ case where the first hurdle is still relevant. Finally, we show that EXP3 and the UCB-based algorithm necessarily cannot perform better than $\sqrt{T}$.