Near-Optimal Pure Exploration in Matrix Games: A Generalization of Stochastic Bandits & Dueling Bandits

We study the sample complexity of identifying the pure strategy Nash equilibrium (PSNE) in a two-player zero-sum matrix game with noise. Formally, we are given a stochastic model where any learner can sample an entry $(i,j)$ of the input matrix $A\in[-1,1]^{n\times m}$ and observe $A_{i,j}+\eta$ where $\eta$ is a zero-mean 1-sub-Gaussian noise. The aim of the learner is to identify the PSNE of $A$, whenever it exists, with high probability while taking as few samples as possible. Zhou et al. (2017) presents an instance-dependent sample complexity lower bound that depends only on the entries in the row and column in which the PSNE lies. We design a near-optimal algorithm whose sample complexity matches the lower bound, up to log factors. The problem of identifying the PSNE also generalizes the problem of pure exploration in stochastic multi-armed bandits and dueling bandits, and our result matches the optimal bounds, up to log factors, in both the settings.

Learning Linear Dynamical Systems with Semi-Parametric Least Squares

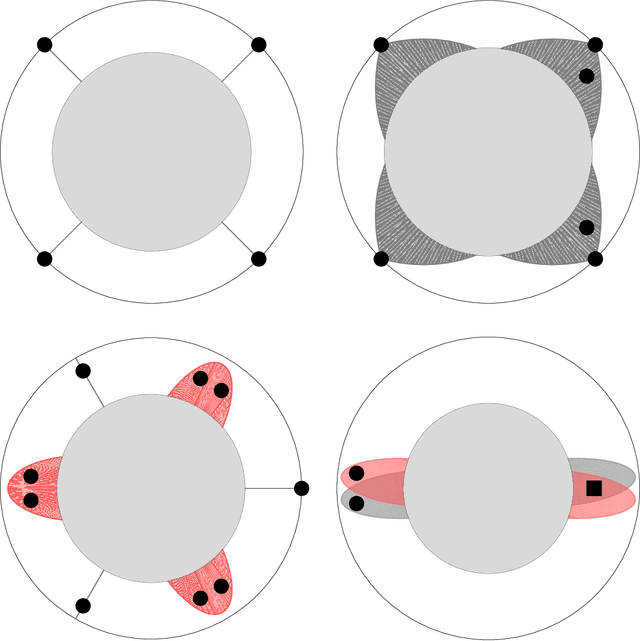
We analyze a simple prefiltered variation of the least squares estimator for the problem of estimation with biased, semi-parametric noise, an error model studied more broadly in causal statistics and active learning. We prove an oracle inequality which demonstrates that this procedure provably mitigates the variance introduced by long-term dependencies. We then demonstrate that prefiltered least squares yields, to our knowledge, the first algorithm that provably estimates the parameters of partially-observed linear systems that attains rates which do not not incur a worst-case dependence on the rate at which these dependencies decay. The algorithm is provably consistent even for systems which satisfy the weaker marginal stability condition obeyed by many classical models based on Newtonian mechanics. In this context, our semi-parametric framework yields guarantees for both stochastic and worst-case noise.

Minimax Lower Bounds for $\mathcal{H}_\infty$-Norm Estimation

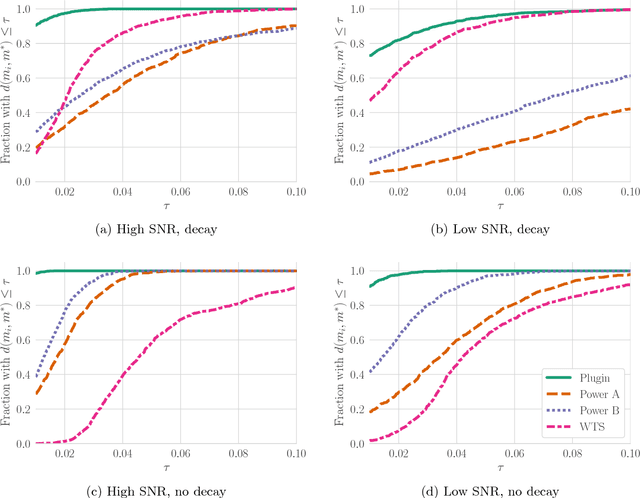
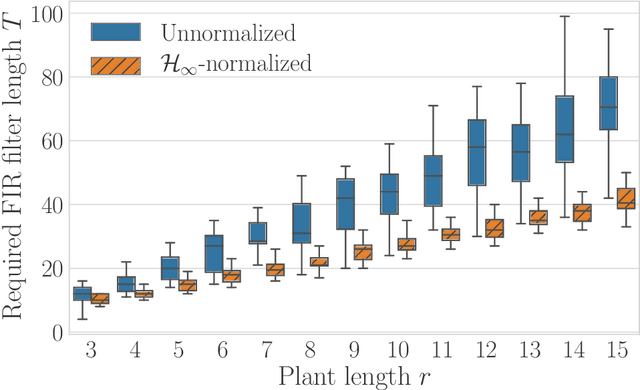
The problem of estimating the $\mathcal{H}_\infty$-norm of an LTI system from noisy input/output measurements has attracted recent attention as an alternative to parameter identification for bounding unmodeled dynamics in robust control. In this paper, we study lower bounds for $\mathcal{H}_\infty$-norm estimation under a query model where at each iteration the algorithm chooses a bounded input signal and receives the response of the chosen signal corrupted by white noise. We prove that when the underlying system is an FIR filter, $\mathcal{H}_\infty$-norm estimation is no more efficient than model identification for passive sampling. For active sampling, we show that norm estimation is at most a factor of $\log{r}$ more sample efficient than model identification, where $r$ is the length of the filter. We complement our theoretical results with experiments which demonstrate that a simple non-adaptive estimator of the norm is competitive with state-of-the-art adaptive norm estimation algorithms.

Finite-Data Performance Guarantees for the Output-Feedback Control of an Unknown System

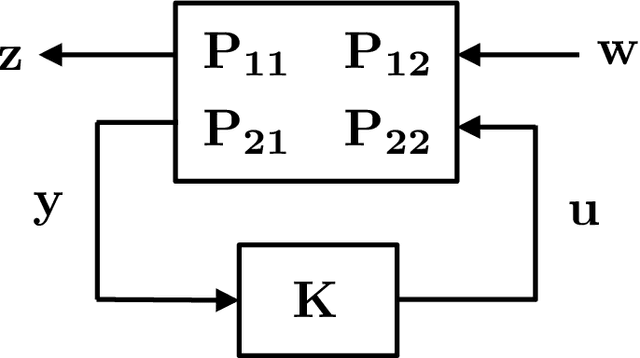
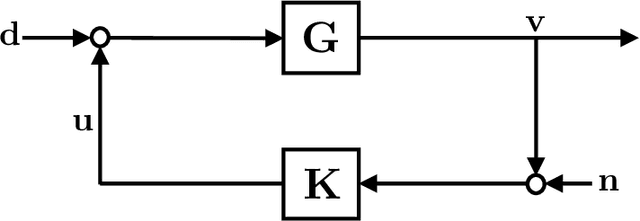
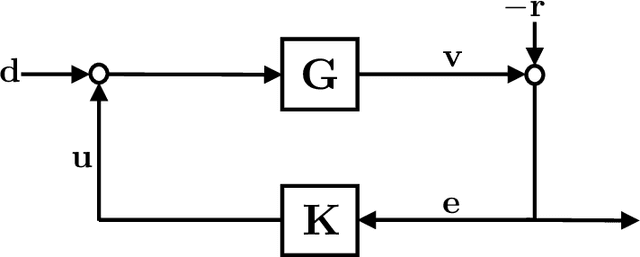
As the systems we control become more complex, first-principle modeling becomes either impossible or intractable, motivating the use of machine learning techniques for the control of systems with continuous action spaces. As impressive as the empirical success of these methods have been, strong theoretical guarantees of performance, safety, or robustness are few and far between. This paper takes a step towards such providing such guarantees by establishing finite-data performance guarantees for the robust output-feedback control of an unknown FIR SISO system. In particular, we introduce the "Coarse-ID control" pipeline, which is composed of a system identification step followed by a robust controller synthesis procedure, and analyze its end-to-end performance, providing quantitative bounds on the performance degradation suffered due to model uncertainty as a function of the number of experiments run to identify the system. We conclude with numerical examples demonstrating the effectiveness of our method.

Non-Asymptotic Analysis of Robust Control from Coarse-Grained Identification

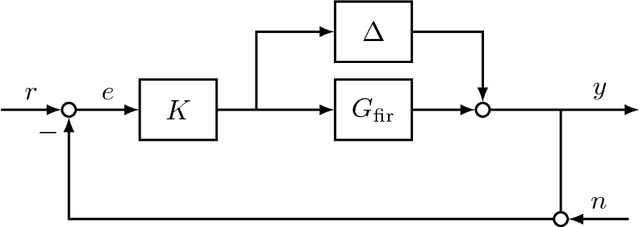
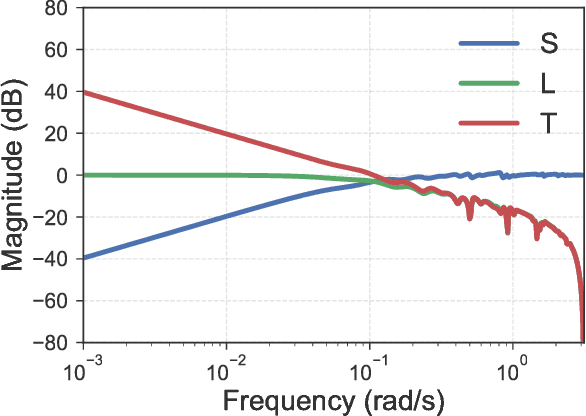
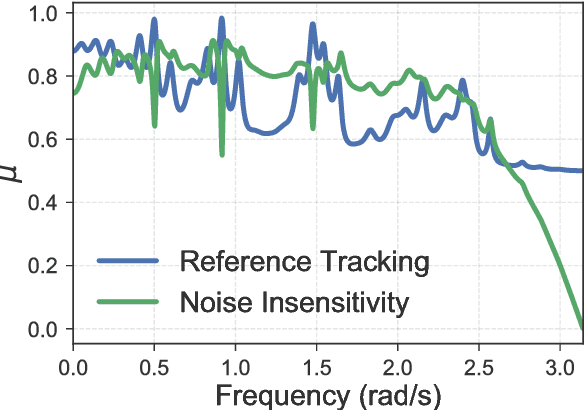
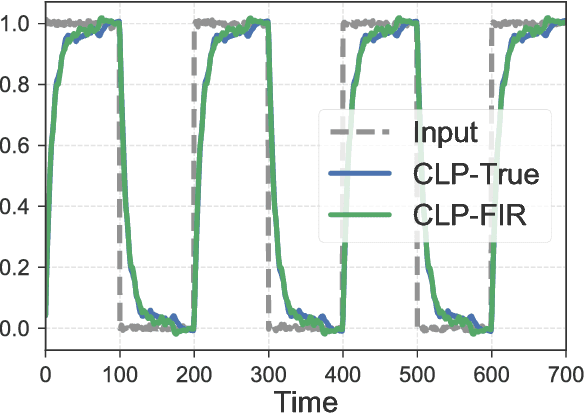
This work explores the trade-off between the number of samples required to accurately build models of dynamical systems and the degradation of performance in various control objectives due to a coarse approximation. In particular, we show that simple models can be easily fit from input/output data and are sufficient for achieving various control objectives. We derive bounds on the number of noisy input/output samples from a stable linear time-invariant system that are sufficient to guarantee that the corresponding finite impulse response approximation is close to the true system in the $\mathcal{H}_\infty$-norm. We demonstrate that these demands are lower than those derived in prior art which aimed to accurately identify dynamical models. We also explore how different physical input constraints, such as power constraints, affect the sample complexity. Finally, we show how our analysis fits within the established framework of robust control, by demonstrating how a controller designed for an approximate system provably meets performance objectives on the true system.