Minimax Lower Bounds for $\mathcal{H}_\infty$-Norm Estimation
Paper and Code
Sep 28, 2018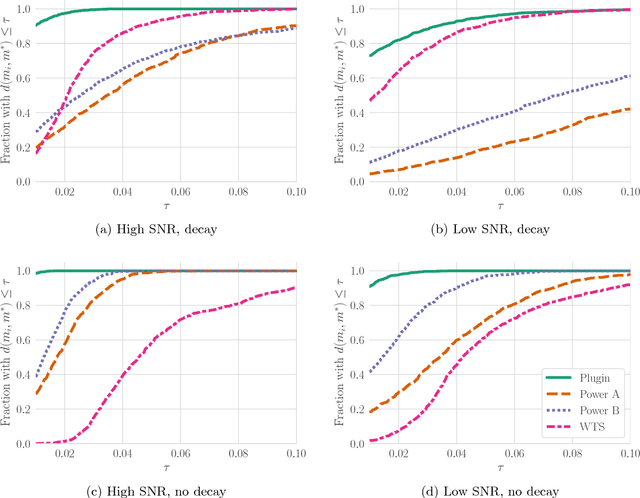
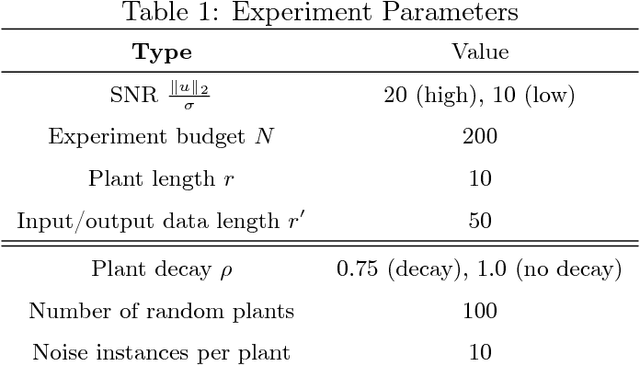
The problem of estimating the $\mathcal{H}_\infty$-norm of an LTI system from noisy input/output measurements has attracted recent attention as an alternative to parameter identification for bounding unmodeled dynamics in robust control. In this paper, we study lower bounds for $\mathcal{H}_\infty$-norm estimation under a query model where at each iteration the algorithm chooses a bounded input signal and receives the response of the chosen signal corrupted by white noise. We prove that when the underlying system is an FIR filter, $\mathcal{H}_\infty$-norm estimation is no more efficient than model identification for passive sampling. For active sampling, we show that norm estimation is at most a factor of $\log{r}$ more sample efficient than model identification, where $r$ is the length of the filter. We complement our theoretical results with experiments which demonstrate that a simple non-adaptive estimator of the norm is competitive with state-of-the-art adaptive norm estimation algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge