Non-Asymptotic Analysis of Robust Control from Coarse-Grained Identification
Paper and Code
Nov 30, 2017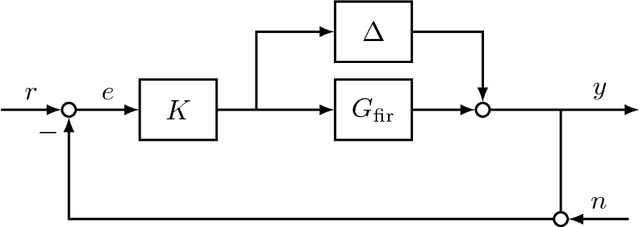
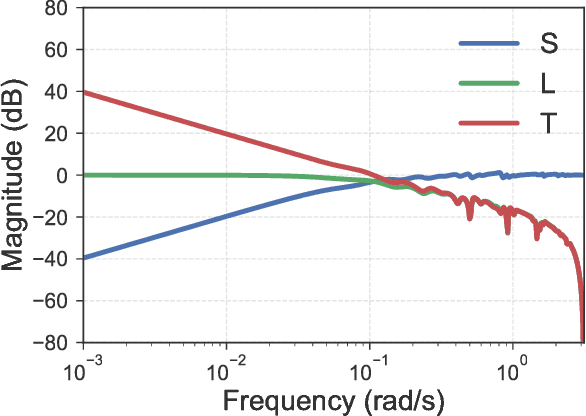
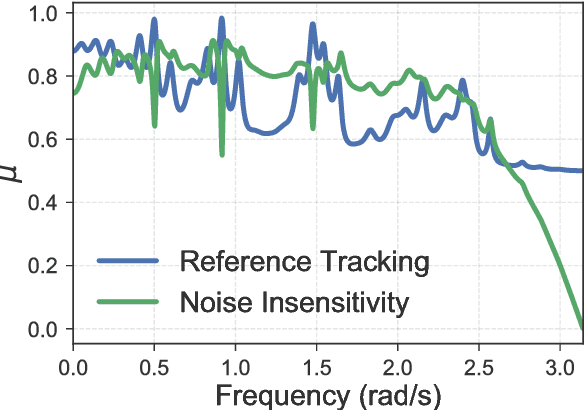
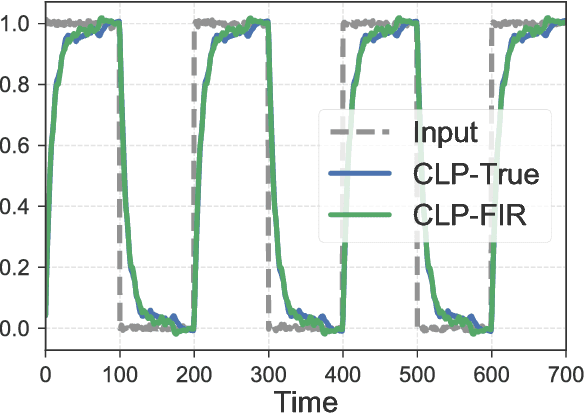
This work explores the trade-off between the number of samples required to accurately build models of dynamical systems and the degradation of performance in various control objectives due to a coarse approximation. In particular, we show that simple models can be easily fit from input/output data and are sufficient for achieving various control objectives. We derive bounds on the number of noisy input/output samples from a stable linear time-invariant system that are sufficient to guarantee that the corresponding finite impulse response approximation is close to the true system in the $\mathcal{H}_\infty$-norm. We demonstrate that these demands are lower than those derived in prior art which aimed to accurately identify dynamical models. We also explore how different physical input constraints, such as power constraints, affect the sample complexity. Finally, we show how our analysis fits within the established framework of robust control, by demonstrating how a controller designed for an approximate system provably meets performance objectives on the true system.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge