Empowering Reliable Visual-Centric Instruction Following in MLLMs

Evaluating the instruction-following (IF) capabilities of Multimodal Large Language Models (MLLMs) is essential for rigorously assessing how faithfully model outputs adhere to user-specified intentions. Nevertheless, existing benchmarks for evaluating MLLMs' instruction-following capability primarily focus on verbal instructions in the textual modality. These limitations hinder a thorough analysis of instruction-following capabilities, as they overlook the implicit constraints embedded in the semantically rich visual modality. To address this gap, we introduce VC-IFEval, a new benchmark accompanied by a systematically constructed dataset that evaluates MLLMs' instruction-following ability under multimodal settings. Our benchmark systematically incorporates vision-dependent constraints into instruction design, enabling a more rigorous and fine-grained assessment of how well MLLMs align their outputs with both visual input and textual instructions. Furthermore, by fine-tuning MLLMs on our dataset, we achieve substantial gains in visual instruction-following accuracy and adherence. Through extensive evaluation across representative MLLMs, we provide new insights into the strengths and limitations of current models.

A Semantically Enhanced Generative Foundation Model Improves Pathological Image Synthesis

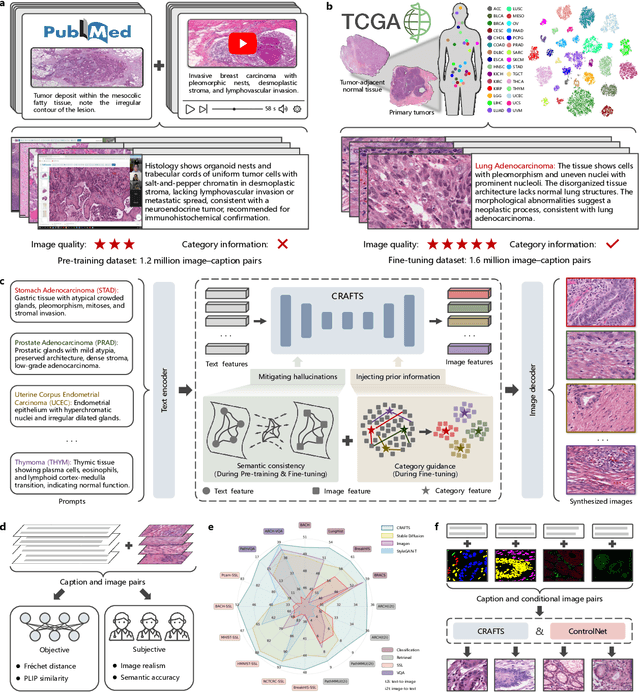
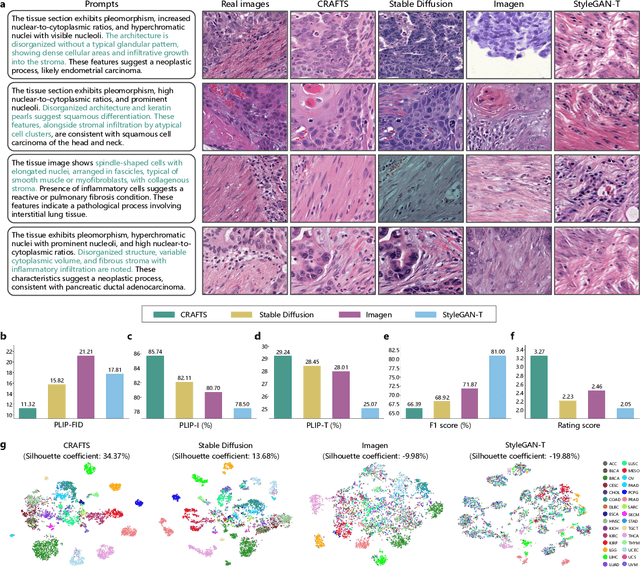
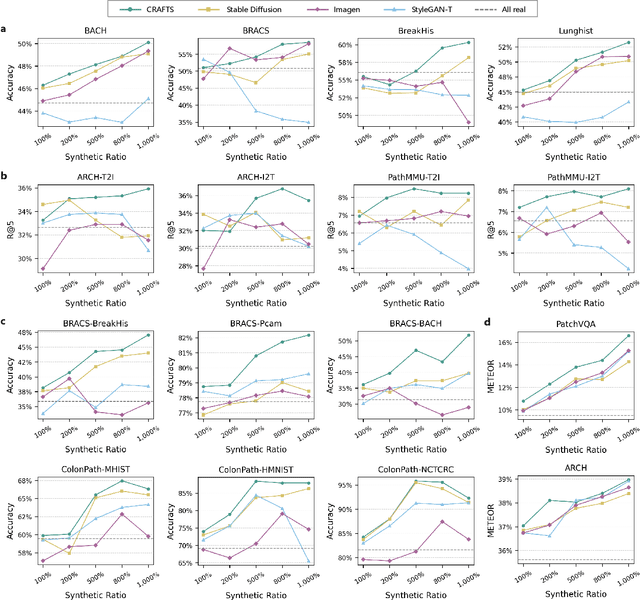
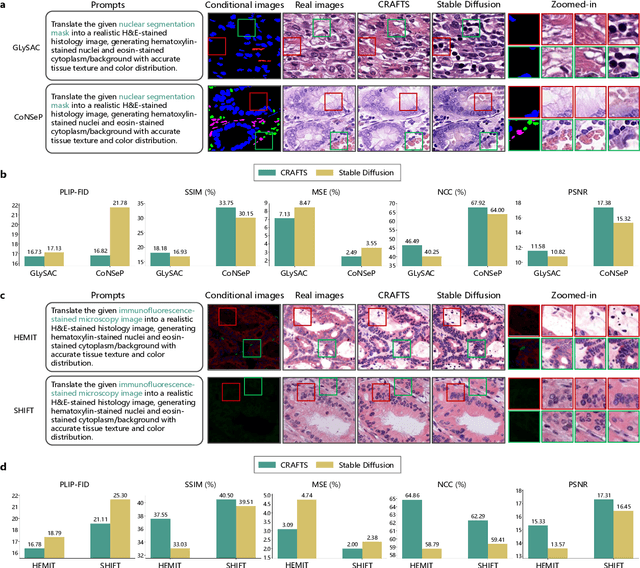
The development of clinical-grade artificial intelligence in pathology is limited by the scarcity of diverse, high-quality annotated datasets. Generative models offer a potential solution but suffer from semantic instability and morphological hallucinations that compromise diagnostic reliability. To address this challenge, we introduce a Correlation-Regulated Alignment Framework for Tissue Synthesis (CRAFTS), the first generative foundation model for pathology-specific text-to-image synthesis. By leveraging a dual-stage training strategy on approximately 2.8 million image-caption pairs, CRAFTS incorporates a novel alignment mechanism that suppresses semantic drift to ensure biological accuracy. This model generates diverse pathological images spanning 30 cancer types, with quality rigorously validated by objective metrics and pathologist evaluations. Furthermore, CRAFTS-augmented datasets enhance the performance across various clinical tasks, including classification, cross-modal retrieval, self-supervised learning, and visual question answering. In addition, coupling CRAFTS with ControlNet enables precise control over tissue architecture from inputs such as nuclear segmentation masks and fluorescence images. By overcoming the critical barriers of data scarcity and privacy concerns, CRAFTS provides a limitless source of diverse, annotated histology data, effectively unlocking the creation of robust diagnostic tools for rare and complex cancer phenotypes.

Scaling Environments for LLM Agents in the Era of Learning from Interaction: A Survey

LLM-based agents can autonomously accomplish complex tasks across various domains. However, to further cultivate capabilities such as adaptive behavior and long-term decision-making, training on static datasets built from human-level knowledge is insufficient. These datasets are costly to construct and lack both dynamism and realism. A growing consensus is that agents should instead interact directly with environments and learn from experience through reinforcement learning. We formalize this iterative process as the Generation-Execution-Feedback (GEF) loop, where environments generate tasks to challenge agents, return observations in response to agents' actions during task execution, and provide evaluative feedback on rollouts for subsequent learning. Under this paradigm, environments function as indispensable producers of experiential data, highlighting the need to scale them toward greater complexity, realism, and interactivity. In this survey, we systematically review representative methods for environment scaling from a pioneering environment-centric perspective and organize them along the stages of the GEF loop, namely task generation, task execution, and feedback. We further analyze benchmarks, implementation strategies, and applications, consolidating fragmented advances and outlining future research directions for agent intelligence.

Diversity-Enhanced Reasoning for Subjective Questions

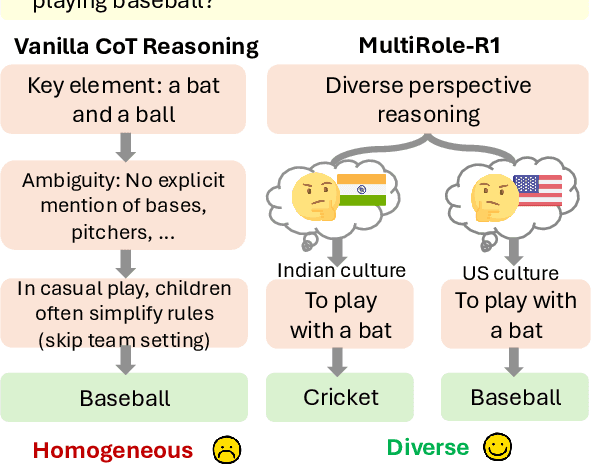
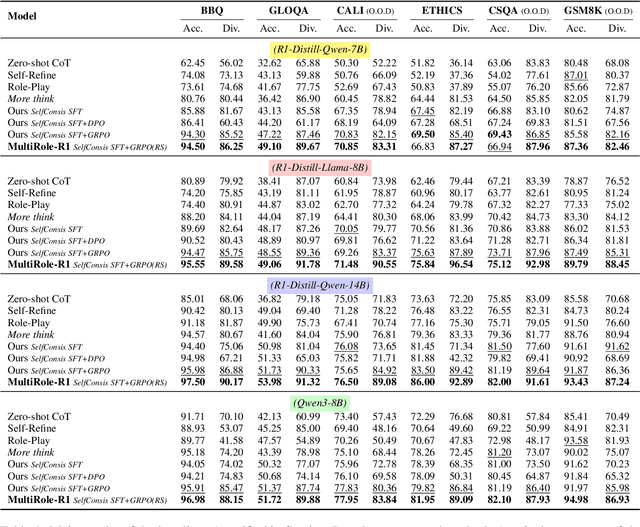
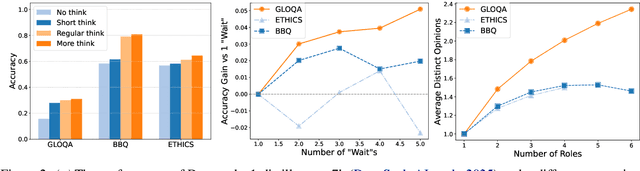
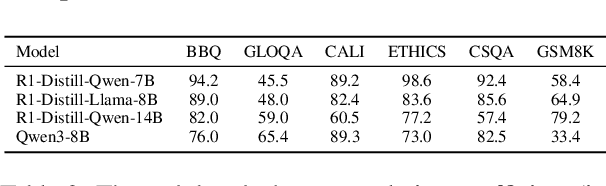
Large reasoning models (LRM) with long chain-of-thought (CoT) capabilities have shown strong performance on objective tasks, such as math reasoning and coding. However, their effectiveness on subjective questions that may have different responses from different perspectives is still limited by a tendency towards homogeneous reasoning, introduced by the reliance on a single ground truth in supervised fine-tuning and verifiable reward in reinforcement learning. Motivated by the finding that increasing role perspectives consistently improves performance, we propose MultiRole-R1, a diversity-enhanced framework with multiple role perspectives, to improve the accuracy and diversity in subjective reasoning tasks. MultiRole-R1 features an unsupervised data construction pipeline that generates reasoning chains that incorporate diverse role perspectives. We further employ reinforcement learning via Group Relative Policy Optimization (GRPO) with reward shaping, by taking diversity as a reward signal in addition to the verifiable reward. With specially designed reward functions, we successfully promote perspective diversity and lexical diversity, uncovering a positive relation between reasoning diversity and accuracy. Our experiment on six benchmarks demonstrates MultiRole-R1's effectiveness and generalizability in enhancing both subjective and objective reasoning, showcasing the potential of diversity-enhanced training in LRMs.

CultureCLIP: Empowering CLIP with Cultural Awareness through Synthetic Images and Contextualized Captions

Pretrained vision-language models (VLMs) such as CLIP excel in multimodal understanding but struggle with contextually relevant fine-grained visual features, making it difficult to distinguish visually similar yet culturally distinct concepts. This limitation stems from the scarcity of high-quality culture-specific datasets, the lack of integrated contextual knowledge, and the absence of hard negatives highlighting subtle distinctions. To address these challenges, we first design a data curation pipeline that leverages open-sourced VLMs and text-to-image diffusion models to construct CulTwin, a synthetic cultural dataset. This dataset consists of paired concept-caption-image triplets, where concepts visually resemble each other but represent different cultural contexts. Then, we fine-tune CLIP on CulTwin to create CultureCLIP, which aligns cultural concepts with contextually enhanced captions and synthetic images through customized contrastive learning, enabling finer cultural differentiation while preserving generalization capabilities. Experiments on culturally relevant benchmarks show that CultureCLIP outperforms the base CLIP, achieving up to a notable 5.49% improvement in fine-grained concept recognition on certain tasks, while preserving CLIP's original generalization ability, validating the effectiveness of our data synthesis and VLM backbone training paradigm in capturing subtle cultural distinctions.

MMBoundary: Advancing MLLM Knowledge Boundary Awareness through Reasoning Step Confidence Calibration

In recent years, multimodal large language models (MLLMs) have made significant progress but continue to face inherent challenges in multimodal reasoning, which requires multi-level (e.g., perception, reasoning) and multi-granular (e.g., multi-step reasoning chain) advanced inferencing. Prior work on estimating model confidence tends to focus on the overall response for training and calibration, but fails to assess confidence in each reasoning step, leading to undesirable hallucination snowballing. In this work, we present MMBoundary, a novel framework that advances the knowledge boundary awareness of MLLMs through reasoning step confidence calibration. To achieve this, we propose to incorporate complementary textual and cross-modal self-rewarding signals to estimate confidence at each step of the MLLM reasoning process. In addition to supervised fine-tuning MLLM on this set of self-rewarded confidence estimation signal for initial confidence expression warm-up, we introduce a reinforcement learning stage with multiple reward functions for further aligning model knowledge and calibrating confidence at each reasoning step, enhancing reasoning chain self-correction. Empirical results show that MMBoundary significantly outperforms existing methods across diverse domain datasets and metrics, achieving an average of 7.5% reduction in multimodal confidence calibration errors and up to 8.3% improvement in task performance.

V$^2$R-Bench: Holistically Evaluating LVLM Robustness to Fundamental Visual Variations

Large Vision Language Models (LVLMs) excel in various vision-language tasks. Yet, their robustness to visual variations in position, scale, orientation, and context that objects in natural scenes inevitably exhibit due to changes in viewpoint and environment remains largely underexplored. To bridge this gap, we introduce V$^2$R-Bench, a comprehensive benchmark framework for evaluating Visual Variation Robustness of LVLMs, which encompasses automated evaluation dataset generation and principled metrics for thorough robustness assessment. Through extensive evaluation on 21 LVLMs, we reveal a surprising vulnerability to visual variations, in which even advanced models that excel at complex vision-language tasks significantly underperform on simple tasks such as object recognition. Interestingly, these models exhibit a distinct visual position bias that contradicts theories of effective receptive fields, and demonstrate a human-like visual acuity threshold. To identify the source of these vulnerabilities, we present a systematic framework for component-level analysis, featuring a novel visualization approach for aligned visual features. Results show that these vulnerabilities stem from error accumulation in the pipeline architecture and inadequate multimodal alignment. Complementary experiments with synthetic data further demonstrate that these limitations are fundamentally architectural deficiencies, scoring the need for architectural innovations in future LVLM designs.

Efficient Near-Optimal Algorithm for Online Shortest Paths in Directed Acyclic Graphs with Bandit Feedback Against Adaptive Adversaries

In this paper, we study the online shortest path problem in directed acyclic graphs (DAGs) under bandit feedback against an adaptive adversary. Given a DAG $G = (V, E)$ with a source node $v_{\mathsf{s}}$ and a sink node $v_{\mathsf{t}}$, let $X \subseteq \{0,1\}^{|E|}$ denote the set of all paths from $v_{\mathsf{s}}$ to $v_{\mathsf{t}}$. At each round $t$, we select a path $\mathbf{x}_t \in X$ and receive bandit feedback on our loss $\langle \mathbf{x}_t, \mathbf{y}_t \rangle \in [-1,1]$, where $\mathbf{y}_t$ is an adversarially chosen loss vector. Our goal is to minimize regret with respect to the best path in hindsight over $T$ rounds. We propose the first computationally efficient algorithm to achieve a near-minimax optimal regret bound of $\tilde O(\sqrt{|E|T\log |X|})$ with high probability against any adaptive adversary, where $\tilde O(\cdot)$ hides logarithmic factors in the number of edges $|E|$. Our algorithm leverages a novel loss estimator and a centroid-based decomposition in a nontrivial manner to attain this regret bound. As an application, we show that our algorithm for DAGs provides state-of-the-art efficient algorithms for $m$-sets, extensive-form games, the Colonel Blotto game, shortest walks in directed graphs, hypercubes, and multi-task multi-armed bandits, achieving improved high-probability regret guarantees in all these settings.

Prototype-Guided Cross-Modal Knowledge Enhancement for Adaptive Survival Prediction

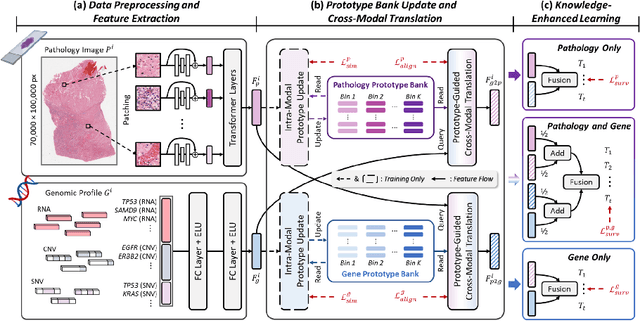
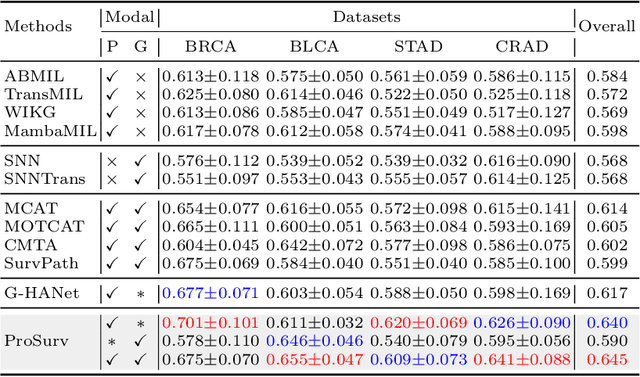
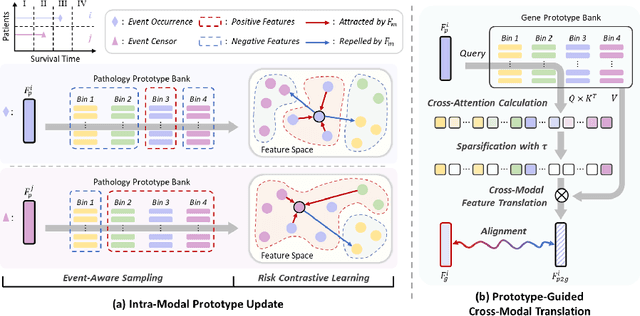
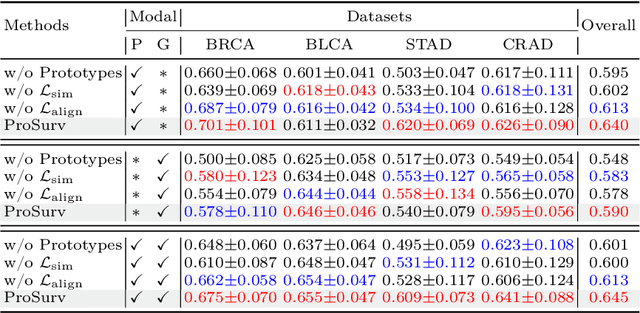
Histo-genomic multimodal survival prediction has garnered growing attention for its remarkable model performance and potential contributions to precision medicine. However, a significant challenge in clinical practice arises when only unimodal data is available, limiting the usability of these advanced multimodal methods. To address this issue, this study proposes a prototype-guided cross-modal knowledge enhancement (ProSurv) framework, which eliminates the dependency on paired data and enables robust learning and adaptive survival prediction. Specifically, we first introduce an intra-modal updating mechanism to construct modality-specific prototype banks that encapsulate the statistics of the whole training set and preserve the modality-specific risk-relevant features/prototypes across intervals. Subsequently, the proposed cross-modal translation module utilizes the learned prototypes to enhance knowledge representation for multimodal inputs and generate features for missing modalities, ensuring robust and adaptive survival prediction across diverse scenarios. Extensive experiments on four public datasets demonstrate the superiority of ProSurv over state-of-the-art methods using either unimodal or multimodal input, and the ablation study underscores its feasibility for broad applicability. Overall, this study addresses a critical practical challenge in computational pathology, offering substantial significance and potential impact in the field.

CALM: Unleashing the Cross-Lingual Self-Aligning Ability of Language Model Question Answering

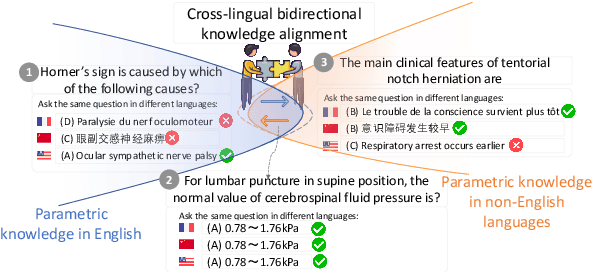
Large Language Models (LLMs) are pretrained on extensive multilingual corpora to acquire both language-specific cultural knowledge and general knowledge. Ideally, while LLMs should provide consistent responses to culture-independent questions across languages, we observe significant performance disparities. To address this, we explore the Cross-Lingual Self-Aligning ability of Language Models (CALM) to align knowledge across languages. Specifically, for a given question, we sample multiple responses across different languages, and select the most self-consistent response as the target, leaving the remaining responses as negative examples. We then employ direct preference optimization (DPO) to align the model's knowledge across different languages. Evaluations on the MEDQA and X-CSQA datasets demonstrate CALM's effectiveness in enhancing cross-lingual knowledge question answering, both in zero-shot and retrieval augmented settings. We also found that increasing the number of languages involved in CALM training leads to even higher accuracy and consistency. We offer a qualitative analysis of how cross-lingual consistency can enhance knowledge alignment and explore the method's generalizability. The source code and data of this paper are available on GitHub.