Effect of Adaptation Rate and Cost Display in a Human-AI Interaction Game

As interactions between humans and AI become more prevalent, it is critical to have better predictors of human behavior in these interactions. We investigated how changes in the AI's adaptive algorithm impact behavior predictions in two-player continuous games. In our experiments, the AI adapted its actions using a gradient descent algorithm under different adaptation rates while human participants were provided cost feedback. The cost feedback was provided by one of two types of visual displays: (a) cost at the current joint action vector, or (b) cost in a local neighborhood of the current joint action vector. Our results demonstrate that AI adaptation rate can significantly affect human behavior, having the ability to shift the outcome between two game theoretic equilibrium. We observed that slow adaptation rates shift the outcome towards the Nash equilibrium, while fast rates shift the outcome towards the human-led Stackelberg equilibrium. The addition of localized cost information had the effect of shifting outcomes towards Nash, compared to the outcomes from cost information at only the current joint action vector. Future work will investigate other effects that influence the convergence of gradient descent games.

Human adaptation to adaptive machines converges to game-theoretic equilibria

Adaptive machines have the potential to assist or interfere with human behavior in a range of contexts, from cognitive decision-making to physical device assistance. Therefore it is critical to understand how machine learning algorithms can influence human actions, particularly in situations where machine goals are misaligned with those of people. Since humans continually adapt to their environment using a combination of explicit and implicit strategies, when the environment contains an adaptive machine, the human and machine play a game. Game theory is an established framework for modeling interactions between two or more decision-makers that has been applied extensively in economic markets and machine algorithms. However, existing approaches make assumptions about, rather than empirically test, how adaptation by individual humans is affected by interaction with an adaptive machine. Here we tested learning algorithms for machines playing general-sum games with human subjects. Our algorithms enable the machine to select the outcome of the co-adaptive interaction from a constellation of game-theoretic equilibria in action and policy spaces. Importantly, the machine learning algorithms work directly from observations of human actions without solving an inverse problem to estimate the human's utility function as in prior work. Surprisingly, one algorithm can steer the human-machine interaction to the machine's optimum, effectively controlling the human's actions even while the human responds optimally to their perceived cost landscape. Our results show that game theory can be used to predict and design outcomes of co-adaptive interactions between intelligent humans and machines.

Convergence Analysis of Gradient-Based Learning with Non-Uniform Learning Rates in Non-Cooperative Multi-Agent Settings

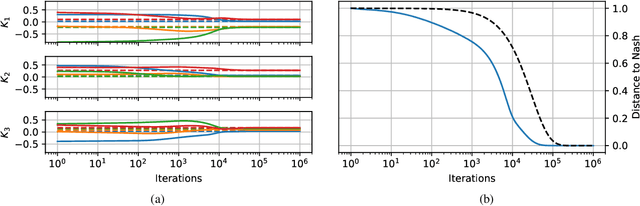
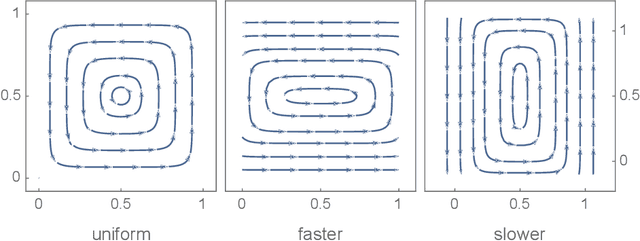
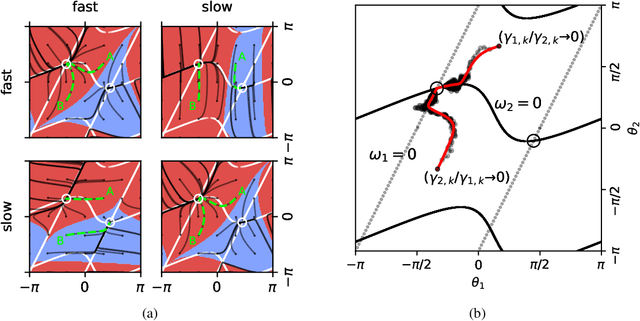
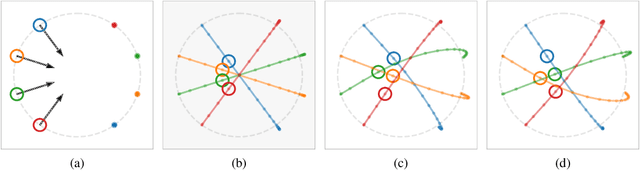
Considering a class of gradient-based multi-agent learning algorithms in non-cooperative settings, we provide local convergence guarantees to a neighborhood of a stable local Nash equilibrium. In particular, we consider continuous games where agents learn in (i) deterministic settings with oracle access to their gradient and (ii) stochastic settings with an unbiased estimator of their gradient. Utilizing the minimum and maximum singular values of the game Jacobian, we provide finite-time convergence guarantees in the deterministic case. On the other hand, in the stochastic case, we provide concentration bounds guaranteeing that with high probability agents will converge to a neighborhood of a stable local Nash equilibrium in finite time. Different than other works in this vein, we also study the effects of non-uniform learning rates on the learning dynamics and convergence rates. We find that much like preconditioning in optimization, non-uniform learning rates cause a distortion in the vector field which can, in turn, change the rate of convergence and the shape of the region of attraction. The analysis is supported by numerical examples that illustrate different aspects of the theory. We conclude with discussion of the results and open questions.

Decoupled limbs yield differentiable trajectory outcomes through intermittent contact in locomotion and manipulation

When limbs are decoupled, we find that trajectory outcomes in mechanical systems subject to unilateral constraints vary differentiably with respect to initial conditions, even as the contact mode sequence varies.

Piecewise-differentiable trajectory outcomes in mechanical systems subject to unilateral constraints

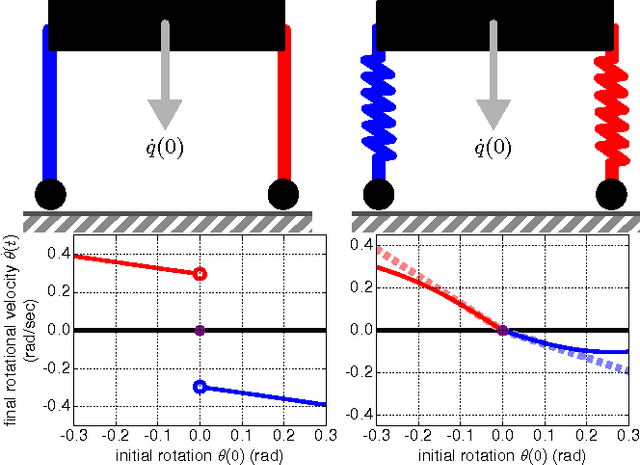
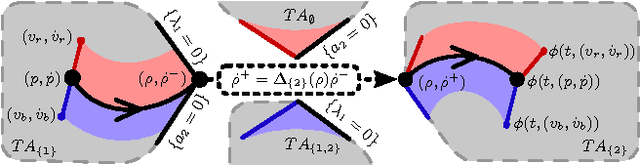
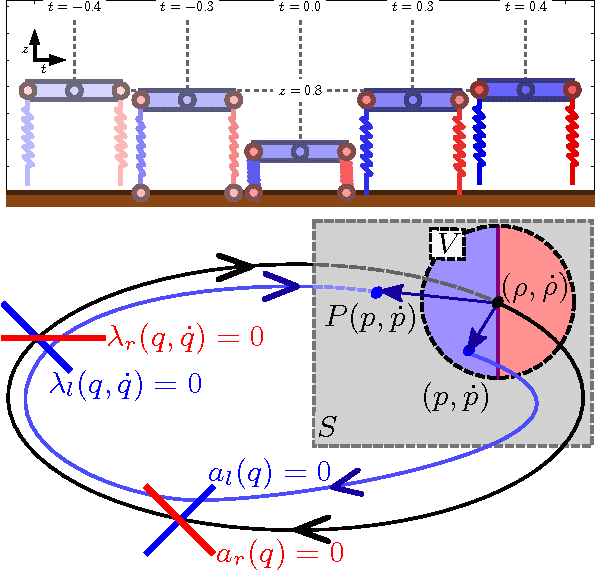
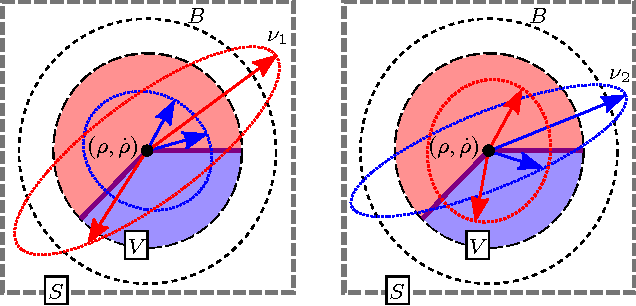
We provide conditions under which trajectory outcomes in mechanical systems subject to unilateral constraints depend piecewise-differentiably on initial conditions, even as the sequence of constraint activations and deactivations varies. This builds on prior work that provided conditions ensuring existence, uniqueness, and continuity of trajectory outcomes, and extends previous differentiability results that applied only to fixed constraint (de)activation sequences. We discuss extensions of our result and implications for assessing stability and controllability.

A Hybrid Dynamical Extension of Averaging

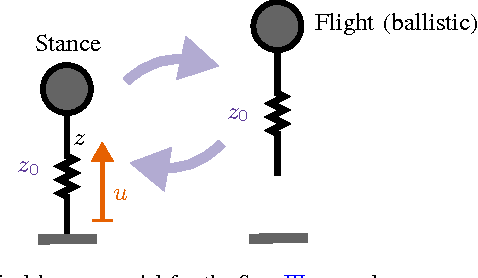
We extend a smooth dynamical systems averaging technique to a class of hybrid systems with a limit cycle that is particularly relevant to the synthesis of stable legged gaits. After introducing a definition of hybrid averageability sufficient to recover the classical result, we provide a simple illustration of its applicability to legged locomotion and conclude with some rather more speculative remarks concerning the prospects for further generalization of these ideas.

A Hybrid Systems Model for Simple Manipulation and Self-Manipulation Systems

Rigid bodies, plastic impact, persistent contact, Coulomb friction, and massless limbs are ubiquitous simplifications introduced to reduce the complexity of mechanics models despite the obvious physical inaccuracies that each incurs individually. In concert, it is well known that the interaction of such idealized approximations can lead to conflicting and even paradoxical results. As robotics modeling moves from the consideration of isolated behaviors to the analysis of tasks requiring their composition, a mathematically tractable framework for building models that combine these simple approximations yet achieve reliable results is overdue. In this paper we present a formal hybrid dynamical system model that introduces suitably restricted compositions of these familiar abstractions with the guarantee of consistency analogous to global existence and uniqueness in classical dynamical systems. The hybrid system developed here provides a discontinuous but self-consistent approximation to the continuous (though possibly very stiff and fast) dynamics of a physical robot undergoing intermittent impacts. The modeling choices sacrifice some quantitative numerical efficiencies while maintaining qualitatively correct and analytically tractable results with consistency guarantees promoting their use in formal reasoning about mechanism, feedback control, and behavior design in robots that make and break contact with their environment.