Stackelberg Actor-Critic: Game-Theoretic Reinforcement Learning Algorithms

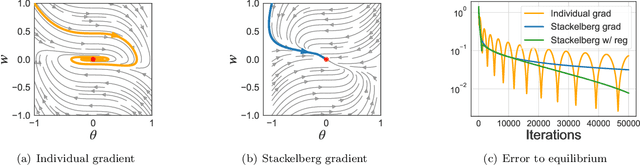
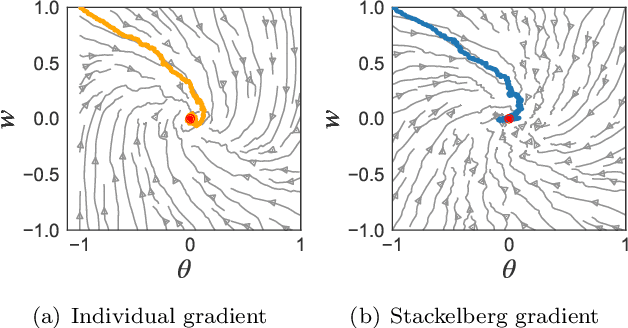
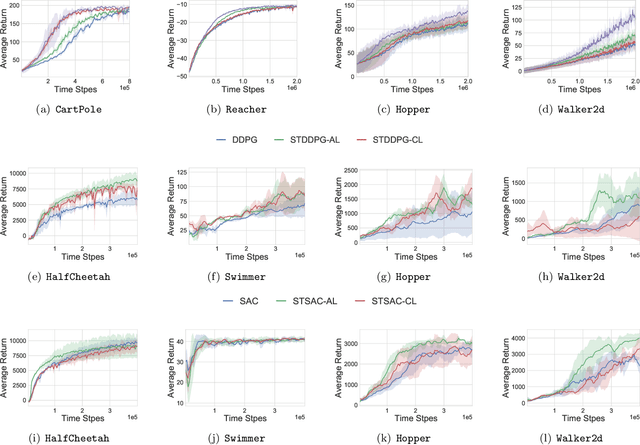
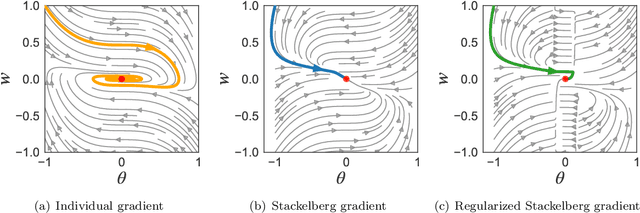
The hierarchical interaction between the actor and critic in actor-critic based reinforcement learning algorithms naturally lends itself to a game-theoretic interpretation. We adopt this viewpoint and model the actor and critic interaction as a two-player general-sum game with a leader-follower structure known as a Stackelberg game. Given this abstraction, we propose a meta-framework for Stackelberg actor-critic algorithms where the leader player follows the total derivative of its objective instead of the usual individual gradient. From a theoretical standpoint, we develop a policy gradient theorem for the refined update and provide a local convergence guarantee for the Stackelberg actor-critic algorithms to a local Stackelberg equilibrium. From an empirical standpoint, we demonstrate via simple examples that the learning dynamics we study mitigate cycling and accelerate convergence compared to the usual gradient dynamics given cost structures induced by actor-critic formulations. Finally, extensive experiments on OpenAI gym environments show that Stackelberg actor-critic algorithms always perform at least as well and often significantly outperform the standard actor-critic algorithm counterparts.

Convergence of Learning Dynamics in Stackelberg Games

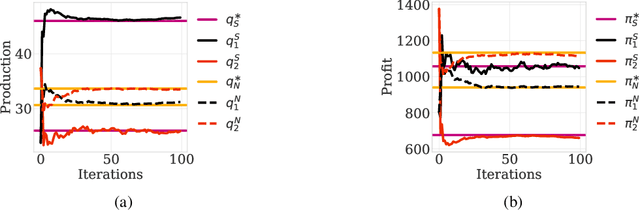
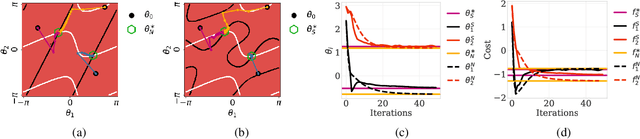
This paper investigates the convergence of learning dynamics in Stackelberg games. In the class of games we consider, there is a hierarchical game being played between a leader and a follower with continuous action spaces. We show that in zero-sum games, the only stable attractors of the Stackelberg gradient dynamics are Stackelberg equilibria. This insight allows us to develop a gradient-based update for the leader that converges to Stackelberg equilibria in zero-sum games and the set of stable attractors in general-sum games. We then consider a follower employing a gradient-play update rule instead of a best response strategy and propose a two-timescale algorithm with similar asymptotic convergence results. For this algorithm, we also provide finite-time high probability bounds for local convergence to a neighborhood of a stable Stackelberg equilibrium in general-sum games.

Convergence Analysis of Gradient-Based Learning with Non-Uniform Learning Rates in Non-Cooperative Multi-Agent Settings

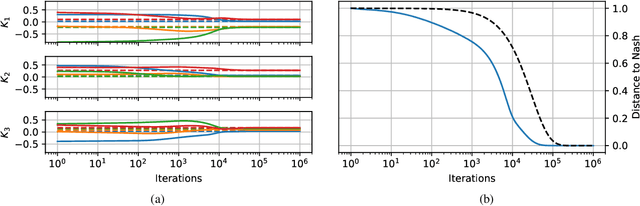
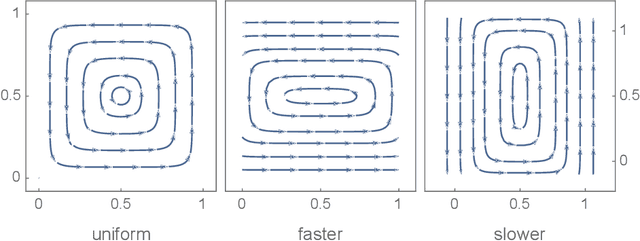
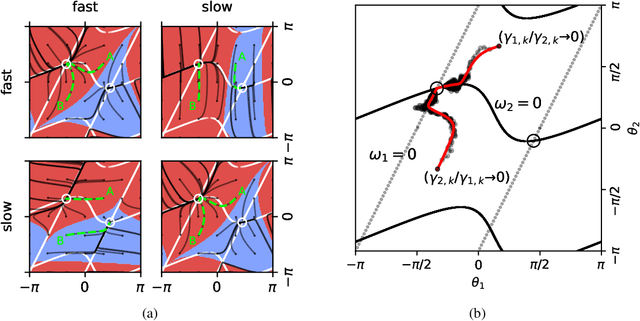
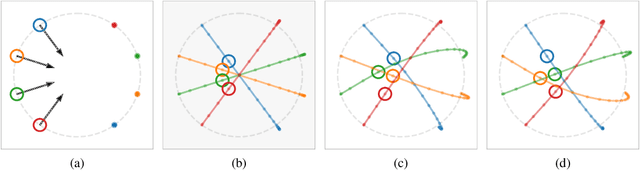
Considering a class of gradient-based multi-agent learning algorithms in non-cooperative settings, we provide local convergence guarantees to a neighborhood of a stable local Nash equilibrium. In particular, we consider continuous games where agents learn in (i) deterministic settings with oracle access to their gradient and (ii) stochastic settings with an unbiased estimator of their gradient. Utilizing the minimum and maximum singular values of the game Jacobian, we provide finite-time convergence guarantees in the deterministic case. On the other hand, in the stochastic case, we provide concentration bounds guaranteeing that with high probability agents will converge to a neighborhood of a stable local Nash equilibrium in finite time. Different than other works in this vein, we also study the effects of non-uniform learning rates on the learning dynamics and convergence rates. We find that much like preconditioning in optimization, non-uniform learning rates cause a distortion in the vector field which can, in turn, change the rate of convergence and the shape of the region of attraction. The analysis is supported by numerical examples that illustrate different aspects of the theory. We conclude with discussion of the results and open questions.