Zane Alumbaugh
Stackelberg Actor-Critic: Game-Theoretic Reinforcement Learning Algorithms
Sep 25, 2021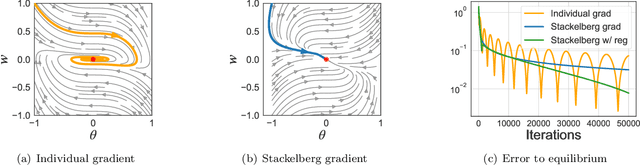
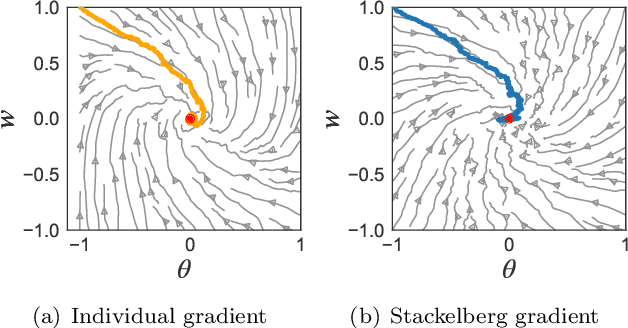
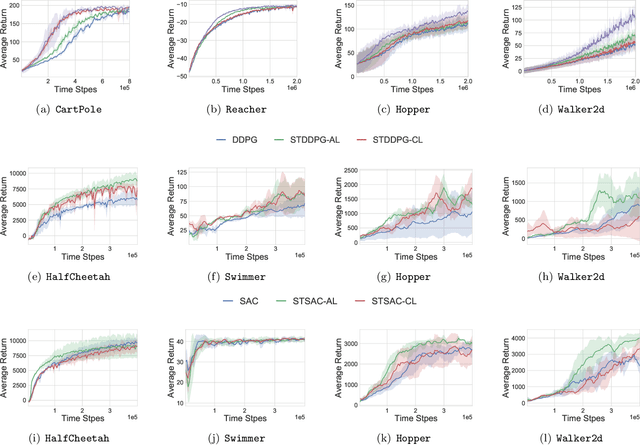
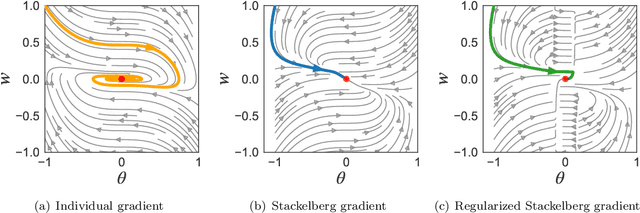
Abstract:The hierarchical interaction between the actor and critic in actor-critic based reinforcement learning algorithms naturally lends itself to a game-theoretic interpretation. We adopt this viewpoint and model the actor and critic interaction as a two-player general-sum game with a leader-follower structure known as a Stackelberg game. Given this abstraction, we propose a meta-framework for Stackelberg actor-critic algorithms where the leader player follows the total derivative of its objective instead of the usual individual gradient. From a theoretical standpoint, we develop a policy gradient theorem for the refined update and provide a local convergence guarantee for the Stackelberg actor-critic algorithms to a local Stackelberg equilibrium. From an empirical standpoint, we demonstrate via simple examples that the learning dynamics we study mitigate cycling and accelerate convergence compared to the usual gradient dynamics given cost structures induced by actor-critic formulations. Finally, extensive experiments on OpenAI gym environments show that Stackelberg actor-critic algorithms always perform at least as well and often significantly outperform the standard actor-critic algorithm counterparts.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge