How to Model Brushless Electric Motors for the Design of Lightweight Robotic Systems

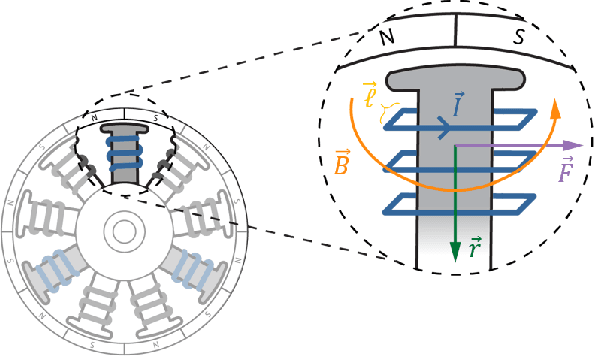
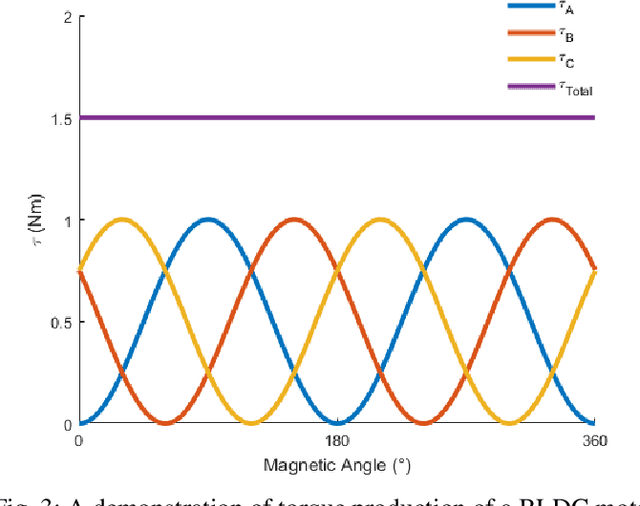
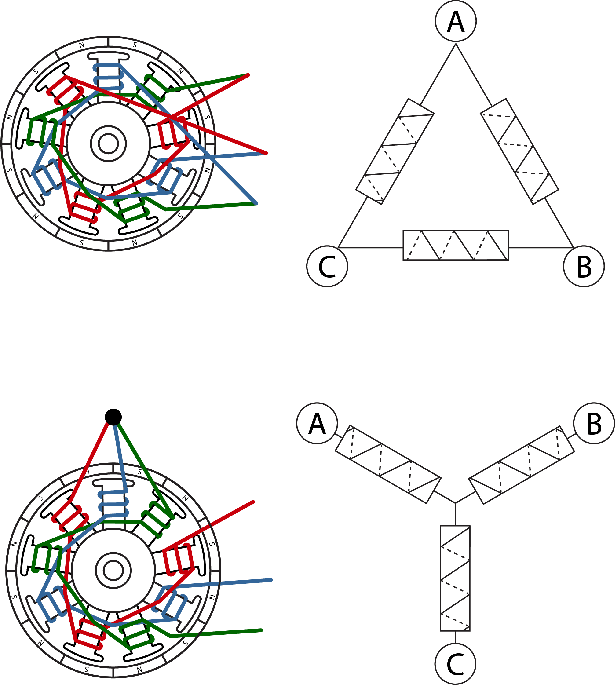
A key step in the development of lightweight, high performance robotic systems is the modeling and selection of permanent magnet brushless direct current (BLDC) electric motors. Typical modeling analyses are completed a priori, and provide insight for properly sizing a motor for an application, specifying the required operating voltage and current, as well as assessing the thermal response and other design attributes (e.g.transmission ratio). However, to perform these modeling analyses, proper information about the motor's characteristics are needed, which are often obtained from manufacturer datasheets. Through our own experience and communications with manufacturers, we have noticed a lack of clarity and standardization in modeling BLDC motors, compounded by vague or inconsistent terminology used in motor datasheets. The purpose of this tutorial is to concisely describe the governing equations for BLDC motor analyses used in the design process, as well as highlight potential errors that can arise from incorrect usage. We present a power-invariant conversion from phase and line-to-line reference frames to a familiar q-axis DC motor representation, which provides a ``brushed'' analogue of a three phase BLDC motor that is convenient for analysis and design. We highlight potential errors including incorrect calculations of winding resistive heat loss, improper estimation of motor torque via the motor's torque constant, and incorrect estimation of the required bus voltage or resulting angular velocity limitations. A unified and condensed set of governing equations is available for designers in the Appendix. The intent of this work is to provide a consolidated mathematical foundation for modeling BLDC motors that addresses existing confusion and fosters high performance designs of future robotic systems.

The Penn Jerboa: A Platform for Exploring Parallel Composition of Templates

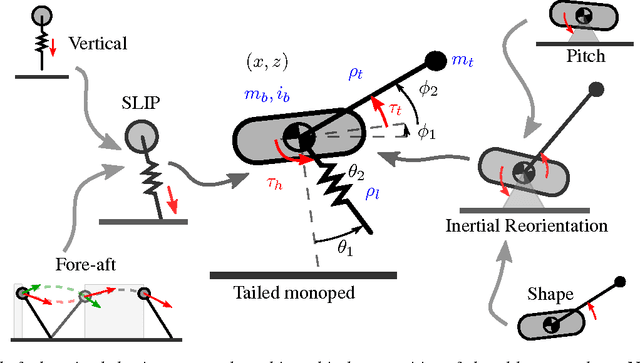
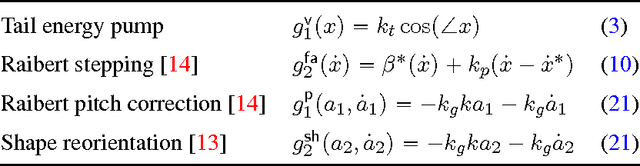
We have built a 12DOF, passive-compliant legged, tailed biped actuated by four brushless DC motors. We anticipate that this machine will achieve varied modes of quasistatic and dynamic balance, enabling a broad range of locomotion tasks including sitting, standing, walking, hopping, running, turning, leaping, and more. Achieving this diversity of behavior with a single under-actuated body, requires a correspondingly diverse array of controllers, motivating our interest in compositional techniques that promote mixing and reuse of a relatively few base constituents to achieve a combinatorially growing array of available choices. Here we report on the development of one important example of such a behavioral programming method, the construction of a novel monopedal sagittal plane hopping gait through parallel composition of four decoupled 1DOF base controllers. For this example behavior, the legs are locked in phase and the body is fastened to a boom to restrict motion to the sagittal plane. The platform's locomotion is powered by the hip motor that adjusts leg touchdown angle in flight and balance in stance, along with a tail motor that adjusts body shape in flight and drives energy into the passive leg shank spring during stance. The motor control signals arise from the application in parallel of four simple, completely decoupled 1DOF feedback laws that provably stabilize in isolation four corresponding 1DOF abstract reference plants. Each of these abstract 1DOF closed loop dynamics represents some simple but crucial specific component of the locomotion task at hand. We present a partial proof of correctness for this parallel composition of template reference systems along with data from the physical platform suggesting these templates are anchored as evidenced by the correspondence of their characteristic motions with a suitably transformed image of traces from the physical platform.

A Hybrid Dynamical Extension of Averaging

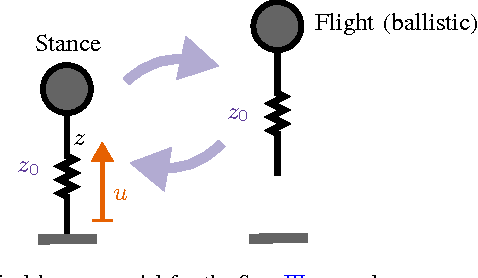
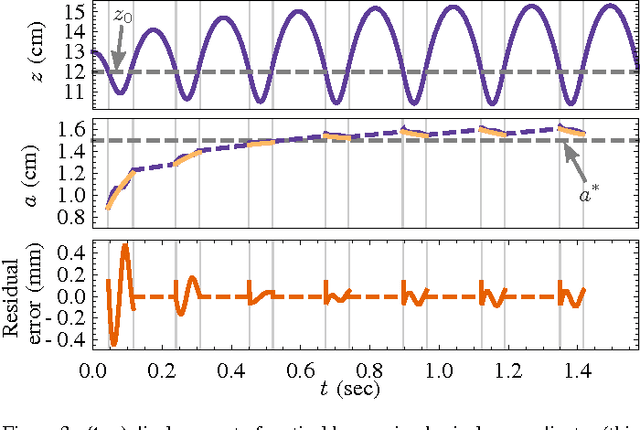
We extend a smooth dynamical systems averaging technique to a class of hybrid systems with a limit cycle that is particularly relevant to the synthesis of stable legged gaits. After introducing a definition of hybrid averageability sufficient to recover the classical result, we provide a simple illustration of its applicability to legged locomotion and conclude with some rather more speculative remarks concerning the prospects for further generalization of these ideas.