A Clinical Tuning Framework for Continuous Kinematic and Impedance Control of a Powered Knee-Ankle Prosthesis

Objective: Configuring a prosthetic leg is an integral part of the fitting process, but the personalization of a multi-modal powered knee-ankle prosthesis is often too complex to realize in a clinical environment. This paper develops both the technical means to individualize a hybrid kinematic-impedance controller for variable-incline walking and sit-stand transitions, and an intuitive Clinical Tuning Interface (CTI) that allows prosthetists to directly modify the controller behavior. Methods: Utilizing an established method for predicting kinematic gait individuality alongside a new parallel approach for kinetic individuality, we applied tuned characteristics exclusively from level-ground walking to personalize continuous-phase/task models of joint kinematics and impedance. To take advantage of this method, we developed a CTI that translates common clinical tuning parameters into model adjustments. We then conducted a case study involving an above-knee amputee participant where a prosthetist iteratively tuned the prosthesis in a simulated clinical session involving walking and sit-stand transitions. Results: The prosthetist fully tuned the multi-activity prosthesis controller in under 20 min. Each iteration of tuning (i.e., observation, parameter adjustment, and model reprocessing) took 2 min on average for walking and 1 min on average for sit-stand. The tuned behavior changes were appropriately manifested in the commanded prosthesis torques, both at the tuned tasks and across untuned tasks (inclines). Conclusion: The CTI leveraged able-bodied trends to efficiently personalize a wide array of walking tasks and sit-stand transitions. A case-study validated the CTI tuning method and demonstrated the efficiency necessary for powered knee-ankle prostheses to become clinically viable.

How to Model Brushless Electric Motors for the Design of Lightweight Robotic Systems

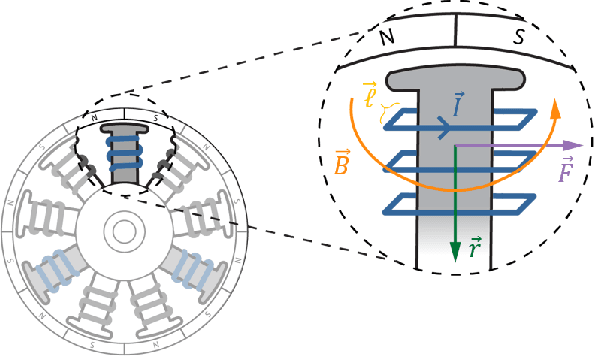
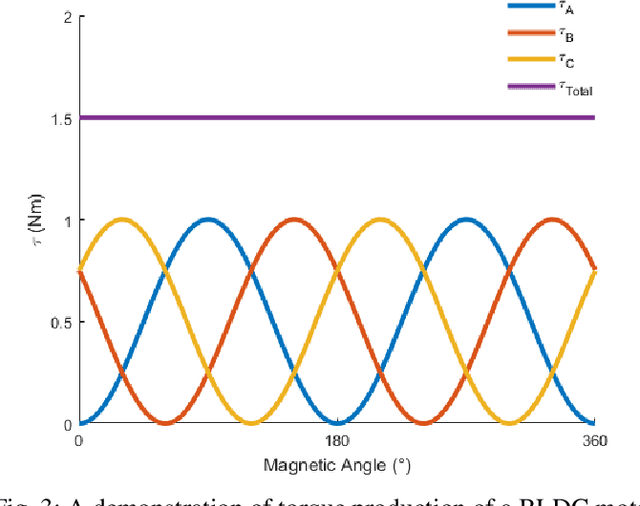
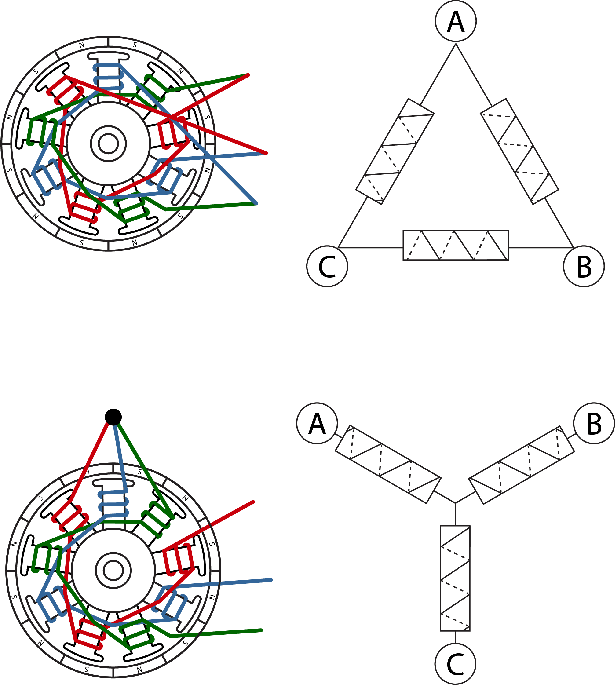
A key step in the development of lightweight, high performance robotic systems is the modeling and selection of permanent magnet brushless direct current (BLDC) electric motors. Typical modeling analyses are completed a priori, and provide insight for properly sizing a motor for an application, specifying the required operating voltage and current, as well as assessing the thermal response and other design attributes (e.g.transmission ratio). However, to perform these modeling analyses, proper information about the motor's characteristics are needed, which are often obtained from manufacturer datasheets. Through our own experience and communications with manufacturers, we have noticed a lack of clarity and standardization in modeling BLDC motors, compounded by vague or inconsistent terminology used in motor datasheets. The purpose of this tutorial is to concisely describe the governing equations for BLDC motor analyses used in the design process, as well as highlight potential errors that can arise from incorrect usage. We present a power-invariant conversion from phase and line-to-line reference frames to a familiar q-axis DC motor representation, which provides a ``brushed'' analogue of a three phase BLDC motor that is convenient for analysis and design. We highlight potential errors including incorrect calculations of winding resistive heat loss, improper estimation of motor torque via the motor's torque constant, and incorrect estimation of the required bus voltage or resulting angular velocity limitations. A unified and condensed set of governing equations is available for designers in the Appendix. The intent of this work is to provide a consolidated mathematical foundation for modeling BLDC motors that addresses existing confusion and fosters high performance designs of future robotic systems.

Minimizing Energy Consumption and Peak Power of Series Elastic Actuators: a Convex Optimization Framework for Elastic Element Design

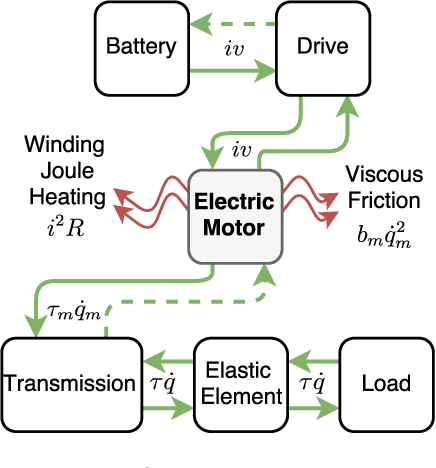
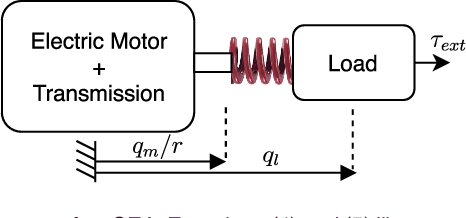
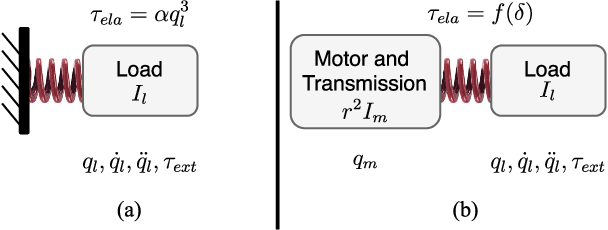
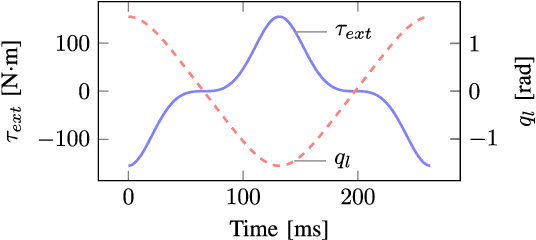
Compared to rigid actuators, Series Elastic Actuators (SEAs) offer a potential reduction of motor energy consumption and peak power, though these benefits are highly dependent on the design of the torque-elongation profile of the elastic element. In the case of linear springs, natural dynamics is a traditional method for this design, but it has two major limitations: arbitrary load trajectories are difficult or impossible to analyze and it does not consider actuator constraints. Parametric optimization is also a popular design method that addresses these limitations, but solutions are only optimal within the space of the parameters. To overcome these limitations, we propose a non-parametric convex optimization program for the design of the nonlinear elastic element that minimizes energy consumption and peak power for an arbitrary periodic reference trajectory. To obtain convexity, we introduce a convex approximation to the expression of peak power; energy consumption is shown to be convex without approximation. The combination of peak power and energy consumption in the cost function leads to a multiobjective convex optimization framework that comprises the main contribution of this paper. As a case study, we recover the elongation-torque profile of a cubic spring, given its natural oscillation as the reference load. We then design nonlinear SEAs for an ankle prosthesis that minimize energy consumption and peak power for different trajectories and extend the range of achievable tasks when subject to actuator constraints.