Robust Optimal Design of Energy Efficient Series Elastic Actuators: Application to a Powered Prosthetic Ankle

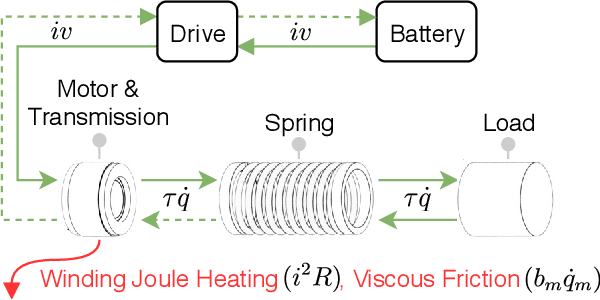
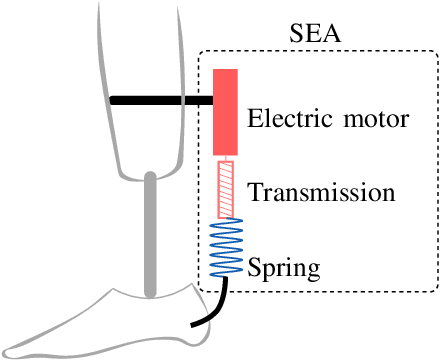
Design of robotic systems that safely and efficiently operate in uncertain operational conditions, such as rehabilitation and physical assistance robots, remains an important challenge in the field. Current methods for the design of energy efficient series elastic actuators use an optimization formulation that typically assumes known operational conditions. This approach could lead to actuators that cannot perform in uncertain environments because elongation, speed, or torque requirements may be beyond actuator specifications when the operation deviates from its nominal conditions. Addressing this gap, we propose a convex optimization formulation to design the stiffness of series elastic actuators to minimize energy consumption and satisfy actuator constraints despite uncertainty due to manufacturing of the spring, unmodeled dynamics, efficiency of the transmission, and the kinematics and kinetics of the load. In our formulation, we express energy consumption as a scalar convex-quadratic function of compliance. In the unconstrained case, this quadratic equation provides an analytical solution to the optimal value of stiffness that minimizes energy consumption for arbitrary periodic reference trajectories. As actuator constraints, we consider peak motor torque, peak motor velocity, limitations due to the speed-torque relationship of DC motors, and peak elongation of the spring. As a simulation case study, we apply our formulation to the robust design of a series elastic actuator for a powered prosthetic ankle. Our simulation results indicate that a small trade-off between energy efficiency and robustness is justified to design actuators that can operate with uncertainty.

Minimizing Energy Consumption and Peak Power of Series Elastic Actuators: a Convex Optimization Framework for Elastic Element Design

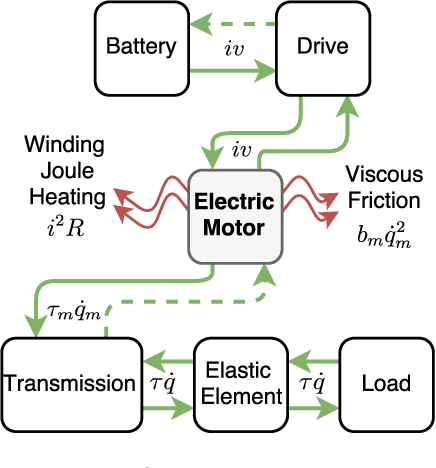
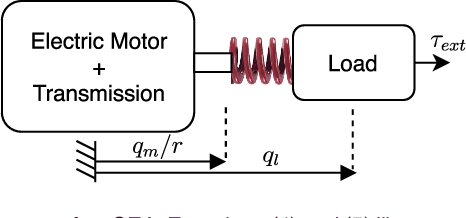
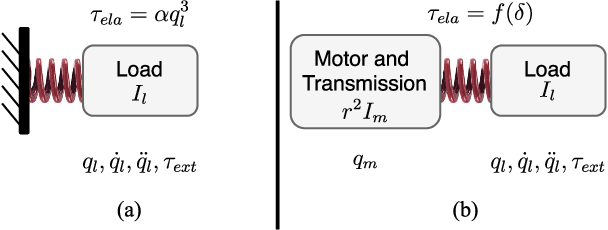
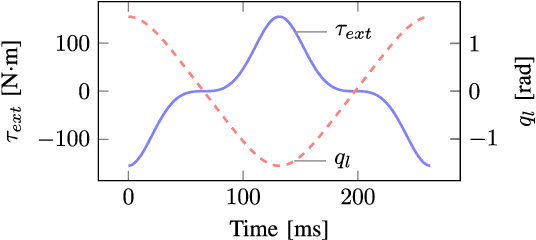
Compared to rigid actuators, Series Elastic Actuators (SEAs) offer a potential reduction of motor energy consumption and peak power, though these benefits are highly dependent on the design of the torque-elongation profile of the elastic element. In the case of linear springs, natural dynamics is a traditional method for this design, but it has two major limitations: arbitrary load trajectories are difficult or impossible to analyze and it does not consider actuator constraints. Parametric optimization is also a popular design method that addresses these limitations, but solutions are only optimal within the space of the parameters. To overcome these limitations, we propose a non-parametric convex optimization program for the design of the nonlinear elastic element that minimizes energy consumption and peak power for an arbitrary periodic reference trajectory. To obtain convexity, we introduce a convex approximation to the expression of peak power; energy consumption is shown to be convex without approximation. The combination of peak power and energy consumption in the cost function leads to a multiobjective convex optimization framework that comprises the main contribution of this paper. As a case study, we recover the elongation-torque profile of a cubic spring, given its natural oscillation as the reference load. We then design nonlinear SEAs for an ankle prosthesis that minimize energy consumption and peak power for different trajectories and extend the range of achievable tasks when subject to actuator constraints.