Decomposing Prediction Mechanisms for In-Context Recall

We introduce a new family of toy problems that combine features of linear-regression-style continuous in-context learning (ICL) with discrete associative recall. We pretrain transformer models on sample traces from this toy, specifically symbolically-labeled interleaved state observations from randomly drawn linear deterministic dynamical systems. We study if the transformer models can recall the state of a sequence previously seen in its context when prompted to do so with the corresponding in-context label. Taking a closer look at this task, it becomes clear that the model must perform two functions: (1) identify which system's state should be recalled and apply that system to its last seen state, and (2) continuing to apply the correct system to predict the subsequent states. Training dynamics reveal that the first capability emerges well into a model's training. Surprisingly, the second capability, of continuing the prediction of a resumed sequence, develops much earlier. Via out-of-distribution experiments, and a mechanistic analysis on model weights via edge pruning, we find that next-token prediction for this toy problem involves at least two separate mechanisms. One mechanism uses the discrete symbolic labels to do the associative recall required to predict the start of a resumption of a previously seen sequence. The second mechanism, which is largely agnostic to the discrete symbolic labels, performs a "Bayesian-style" prediction based on the previous token and the context. These two mechanisms have different learning dynamics. To confirm that this multi-mechanism (manifesting as separate phase transitions) phenomenon is not just an artifact of our toy setting, we used OLMo training checkpoints on an ICL translation task to see a similar phenomenon: a decisive gap in the emergence of first-task-token performance vs second-task-token performance.

Can Custom Models Learn In-Context? An Exploration of Hybrid Architecture Performance on In-Context Learning Tasks

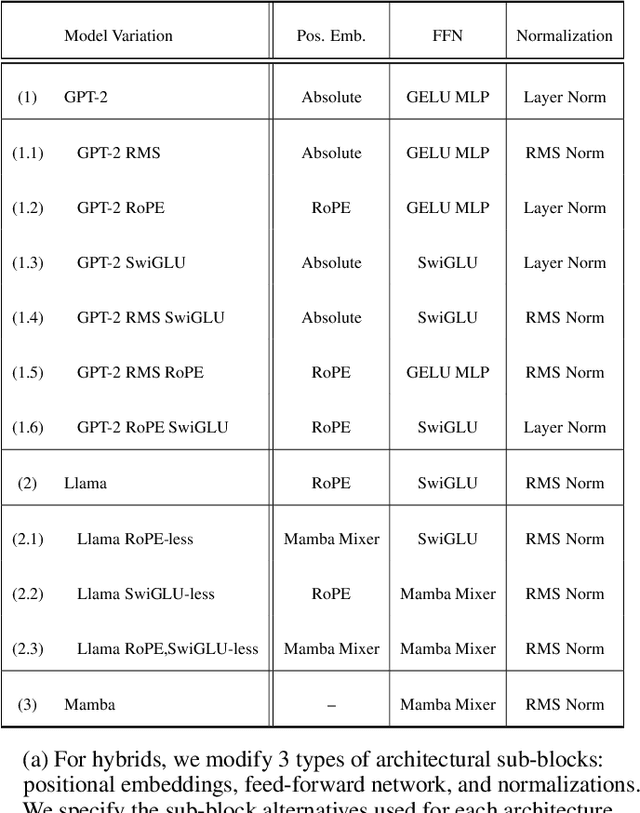
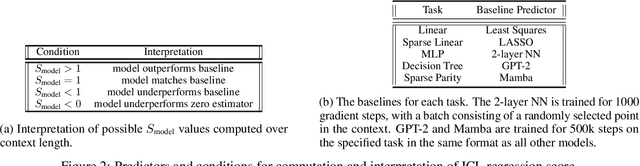
In-Context Learning (ICL) is a phenomenon where task learning occurs through a prompt sequence without the necessity of parameter updates. ICL in Multi-Headed Attention (MHA) with absolute positional embedding has been the focus of more study than other sequence model varieties. We examine implications of architectural differences between GPT-2 and LLaMa as well as LlaMa and Mamba. We extend work done by Garg et al. (2022) and Park et al. (2024) to GPT-2/LLaMa hybrid and LLaMa/Mamba hybrid models - examining the interplay between sequence transformation blocks and regressive performance in-context. We note that certain architectural changes cause degraded training efficiency/ICL accuracy by converging to suboptimal predictors or converging slower. We also find certain hybrids showing optimistic performance improvements, informing potential future ICL-focused architecture modifications. Additionally, we propose the "ICL regression score", a scalar metric describing a model's whole performance on a specific task. Compute limitations impose restrictions on our architecture-space, training duration, number of training runs, function class complexity, and benchmark complexity. To foster reproducible and extensible research, we provide a typed, modular, and extensible Python package on which we run all experiments.

Provable Weak-to-Strong Generalization via Benign Overfitting

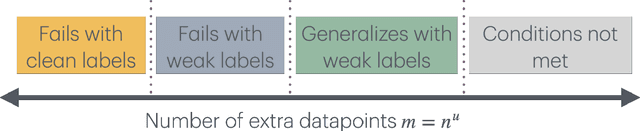
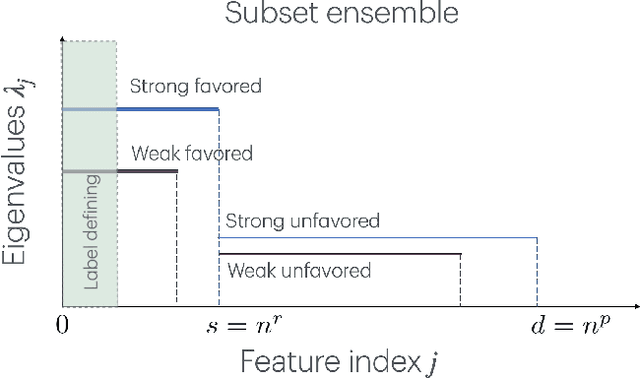
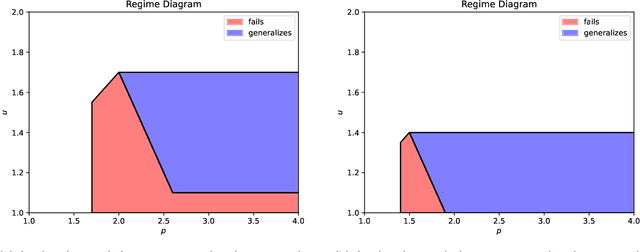
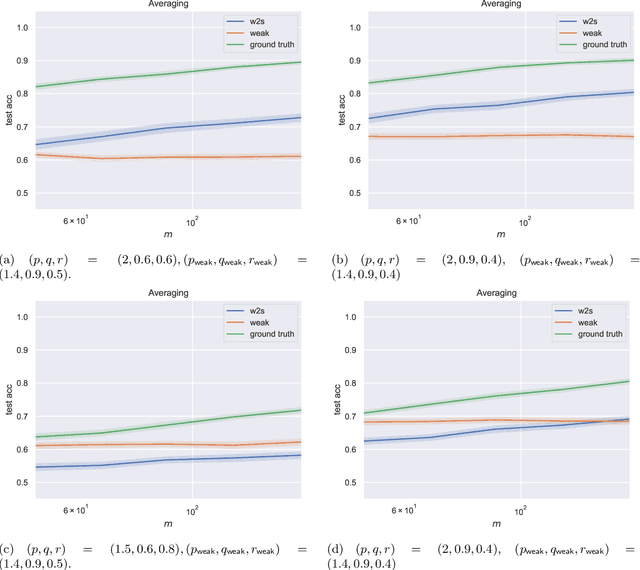
The classic teacher-student model in machine learning posits that a strong teacher supervises a weak student to improve the student's capabilities. We instead consider the inverted situation, where a weak teacher supervises a strong student with imperfect pseudolabels. This paradigm was recently brought forth by Burns et al.'23 and termed \emph{weak-to-strong generalization}. We theoretically investigate weak-to-strong generalization for binary and multilabel classification in a stylized overparameterized spiked covariance model with Gaussian covariates where the weak teacher's pseudolabels are asymptotically like random guessing. Under these assumptions, we provably identify two asymptotic phases of the strong student's generalization after weak supervision: (1) successful generalization and (2) random guessing. Our techniques should eventually extend to weak-to-strong multiclass classification. Towards doing so, we prove a tight lower tail inequality for the maximum of correlated Gaussians, which may be of independent interest. Understanding the multilabel setting reinforces the value of using logits for weak supervision when they are available.

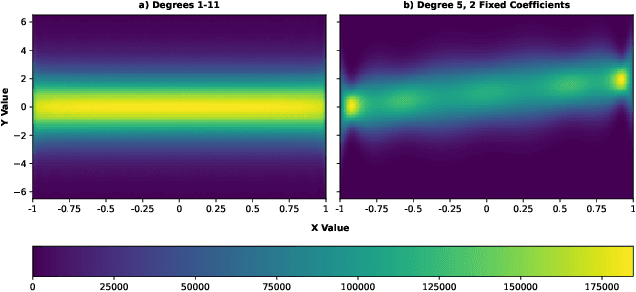
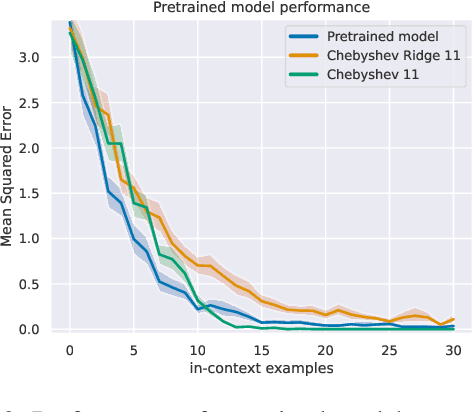
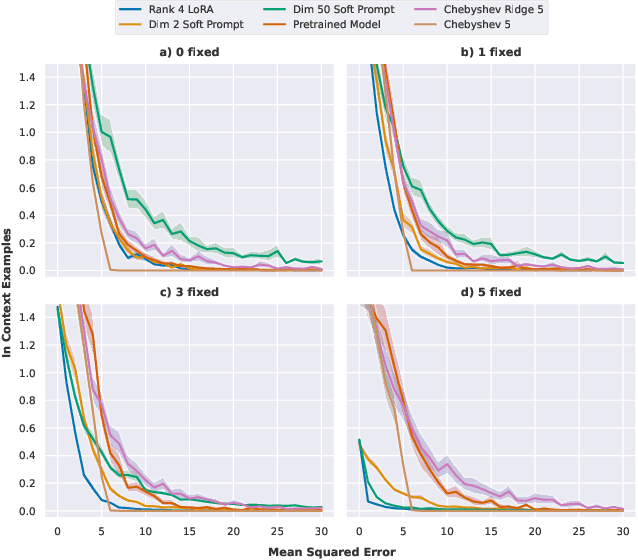
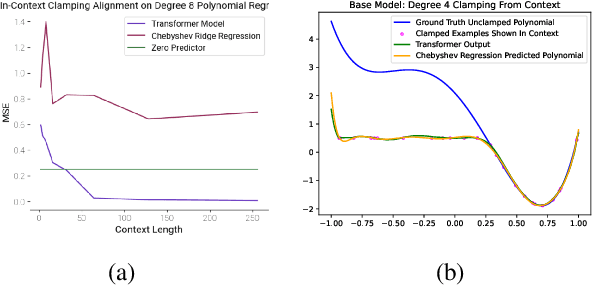
Polynomial Regression as a Task for Understanding In-context Learning Through Finetuning and Alignment

Simple function classes have emerged as toy problems to better understand in-context-learning in transformer-based architectures used for large language models. But previously proposed simple function classes like linear regression or multi-layer-perceptrons lack the structure required to explore things like prompting and alignment within models capable of in-context-learning. We propose univariate polynomial regression as a function class that is just rich enough to study prompting and alignment, while allowing us to visualize and understand what is going on clearly.

Precise Asymptotic Generalization for Multiclass Classification with Overparameterized Linear Models

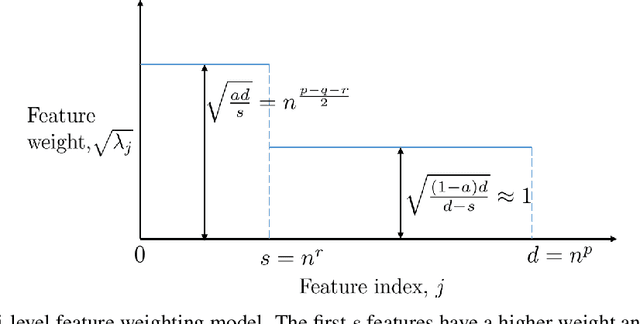
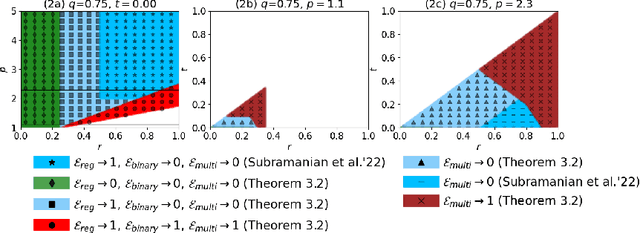
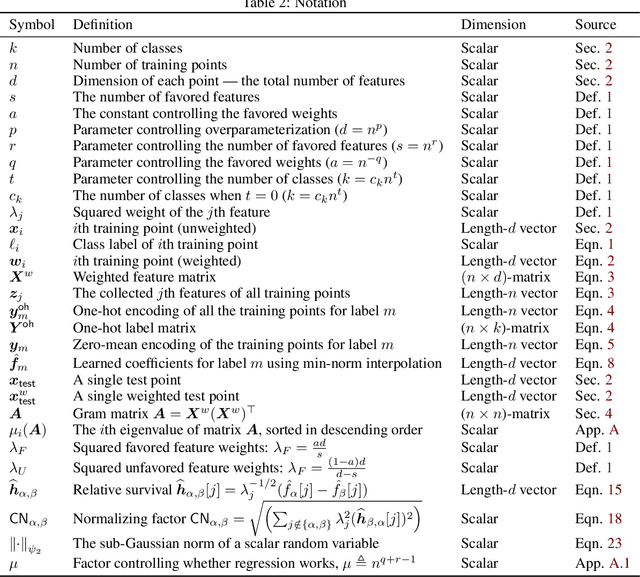
We study the asymptotic generalization of an overparameterized linear model for multiclass classification under the Gaussian covariates bi-level model introduced in Subramanian et al.~'22, where the number of data points, features, and classes all grow together. We fully resolve the conjecture posed in Subramanian et al.~'22, matching the predicted regimes for generalization. Furthermore, our new lower bounds are akin to an information-theoretic strong converse: they establish that the misclassification rate goes to 0 or 1 asymptotically. One surprising consequence of our tight results is that the min-norm interpolating classifier can be asymptotically suboptimal relative to noninterpolating classifiers in the regime where the min-norm interpolating regressor is known to be optimal. The key to our tight analysis is a new variant of the Hanson-Wright inequality which is broadly useful for multiclass problems with sparse labels. As an application, we show that the same type of analysis can be used to analyze the related multilabel classification problem under the same bi-level ensemble.

Generalization for multiclass classification with overparameterized linear models

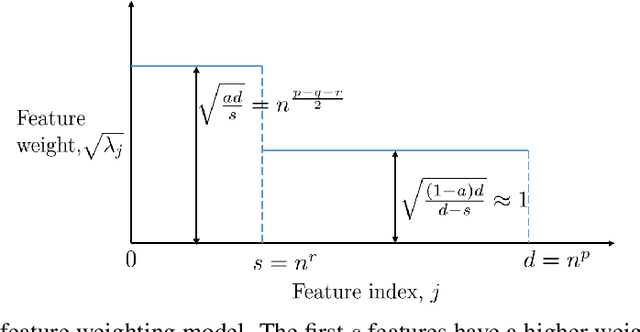
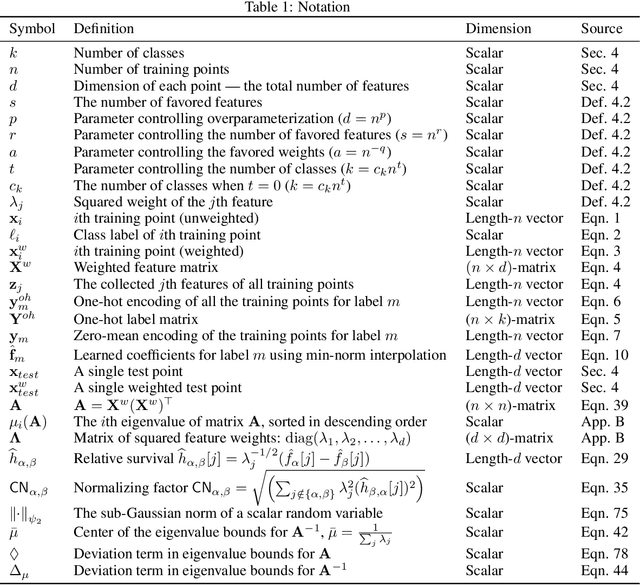
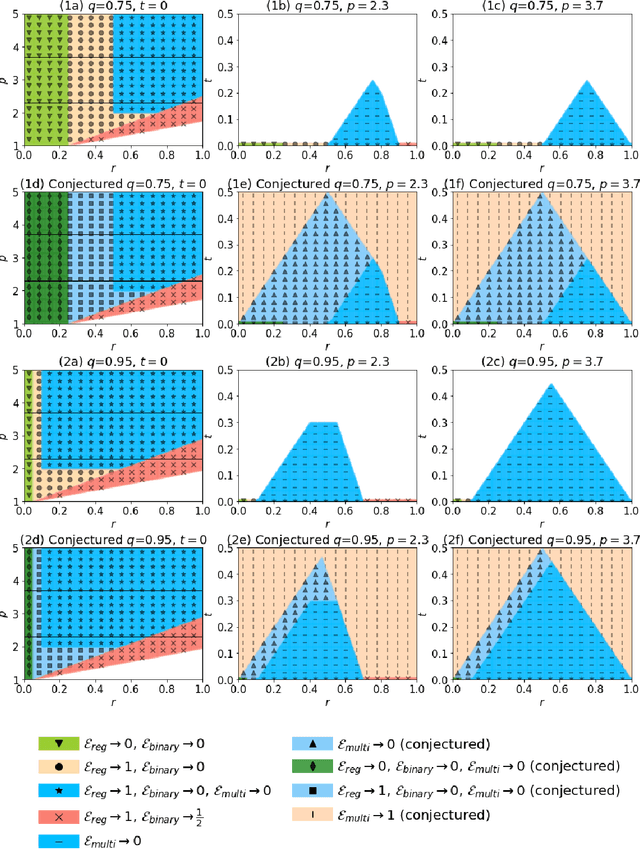
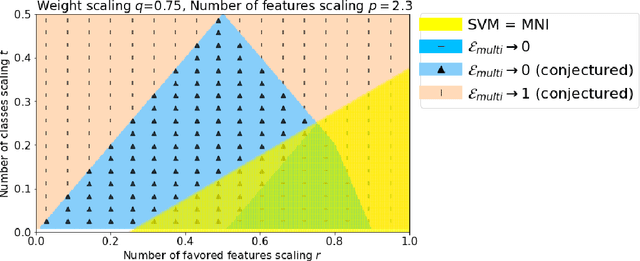
Via an overparameterized linear model with Gaussian features, we provide conditions for good generalization for multiclass classification of minimum-norm interpolating solutions in an asymptotic setting where both the number of underlying features and the number of classes scale with the number of training points. The survival/contamination analysis framework for understanding the behavior of overparameterized learning problems is adapted to this setting, revealing that multiclass classification qualitatively behaves like binary classification in that, as long as there are not too many classes (made precise in the paper), it is possible to generalize well even in some settings where the corresponding regression tasks would not generalize. Besides various technical challenges, it turns out that the key difference from the binary classification setting is that there are relatively fewer positive training examples of each class in the multiclass setting as the number of classes increases, making the multiclass problem "harder" than the binary one.

Classification and Adversarial examples in an Overparameterized Linear Model: A Signal Processing Perspective

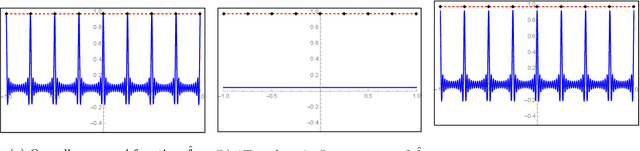
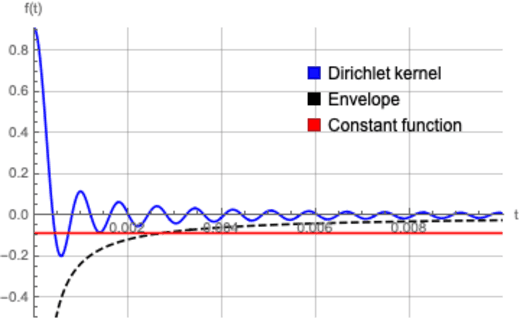
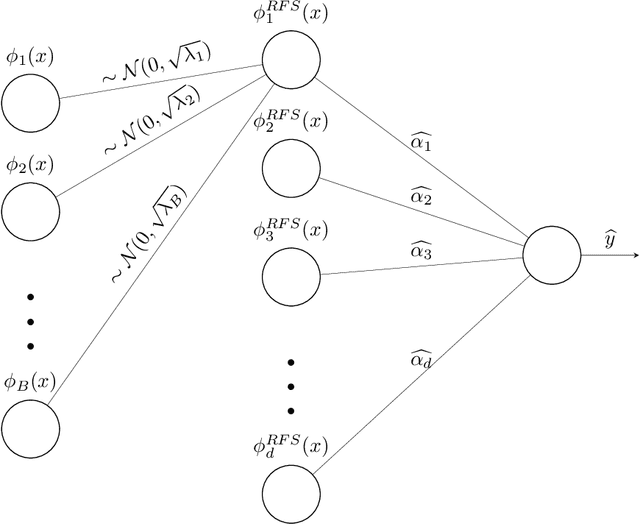
State-of-the-art deep learning classifiers are heavily overparameterized with respect to the amount of training examples and observed to generalize well on "clean" data, but be highly susceptible to infinitesmal adversarial perturbations. In this paper, we identify an overparameterized linear ensemble, that uses the "lifted" Fourier feature map, that demonstrates both of these behaviors. The input is one-dimensional, and the adversary is only allowed to perturb these inputs and not the non-linear features directly. We find that the learned model is susceptible to adversaries in an intermediate regime where classification generalizes but regression does not. Notably, the susceptibility arises despite the absence of model mis-specification or label noise, which are commonly cited reasons for adversarial-susceptibility. These results are extended theoretically to a random-Fourier-sum setup that exhibits double-descent behavior. In both feature-setups, the adversarial vulnerability arises because of a phenomenon we term spatial localization: the predictions of the learned model are markedly more sensitive in the vicinity of training points than elsewhere. This sensitivity is a consequence of feature lifting and is reminiscent of Gibb's and Runge's phenomena from signal processing and functional analysis. Despite the adversarial susceptibility, we find that classification with these features can be easier than the more commonly studied "independent feature" models.

On the Impossibility of Convergence of Mixed Strategies with No Regret Learning

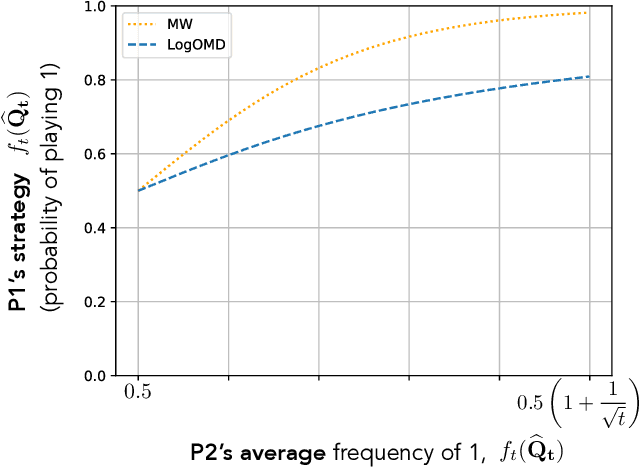
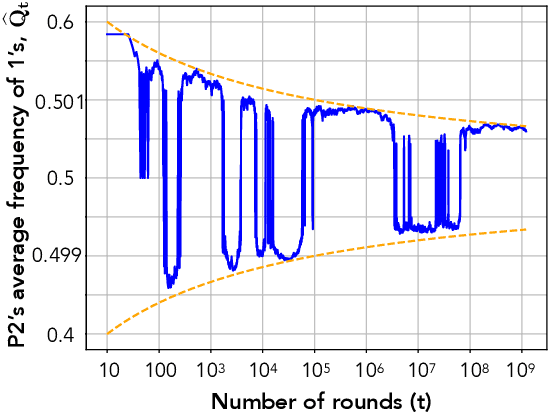
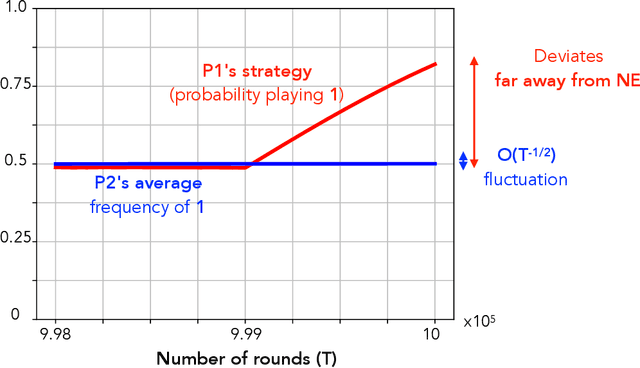
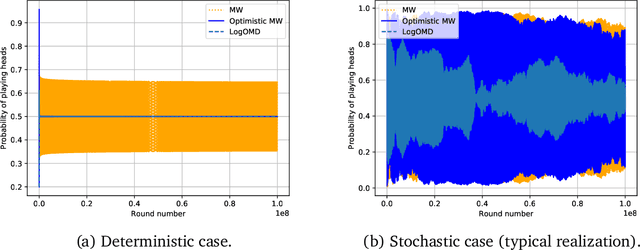
We study convergence properties of the mixed strategies that result from a general class of optimal no regret learning strategies in a repeated game setting where the stage game is any 2 by 2 competitive game (i.e. game for which all the Nash equilibria (NE) of the game are completely mixed). We consider the class of strategies whose information set at each step is the empirical average of the opponent's realized play (and the step number), that we call mean based strategies. We first show that there does not exist any optimal no regret, mean based strategy for player 1 that would result in the convergence of her mixed strategies (in probability) against an opponent that plays his Nash equilibrium mixed strategy at each step. Next, we show that this last iterate divergence necessarily occurs if player 2 uses any adaptive strategy with a minimal randomness property. This property is satisfied, for example, by any fixed sequence of mixed strategies for player 2 that converges to NE. We conjecture that this property holds when both players use optimal no regret learning strategies against each other, leading to the divergence of the mixed strategies with a positive probability. Finally, we show that variants of mean based strategies using recency bias, which have yielded last iterate convergence in deterministic min max optimization, continue to lead to this last iterate divergence. This demonstrates a crucial difference in outcomes between using the opponent's mixtures and realizations to make strategy updates.

Classification vs regression in overparameterized regimes: Does the loss function matter?

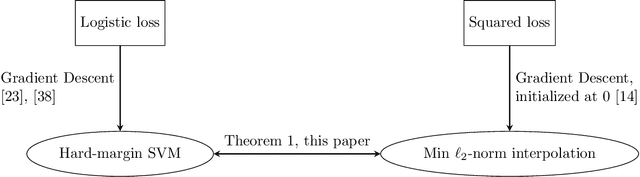
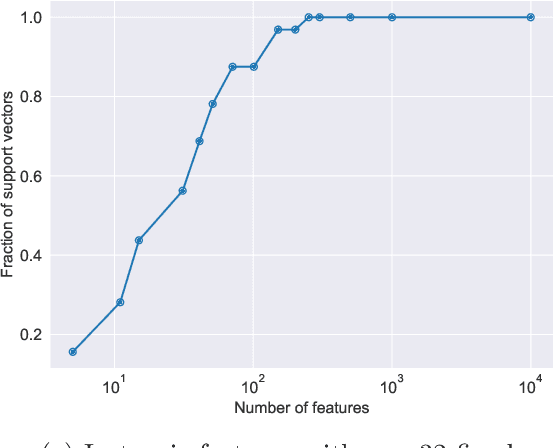
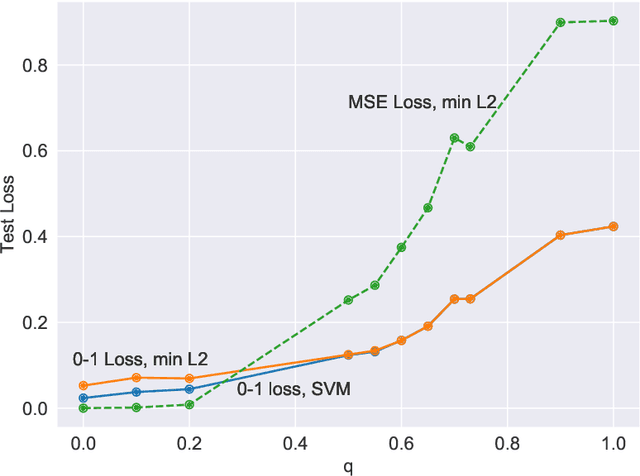
We compare classification and regression tasks in the overparameterized linear model with Gaussian features. On the one hand, we show that with sufficient overparameterization all training points are support vectors: solutions obtained by least-squares minimum-norm interpolation, typically used for regression, are identical to those produced by the hard-margin support vector machine (SVM) that minimizes the hinge loss, typically used for training classifiers. On the other hand, we show that there exist regimes where these solutions are near-optimal when evaluated by the 0-1 test loss function, but do not generalize if evaluated by the square loss function, i.e. they achieve the null risk. Our results demonstrate the very different roles and properties of loss functions used at the training phase (optimization) and the testing phase (generalization).

Harmless interpolation of noisy data in regression

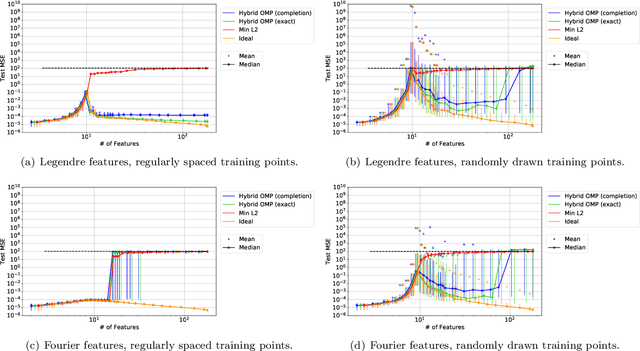
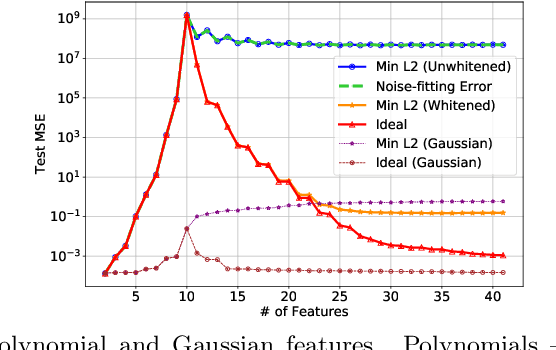
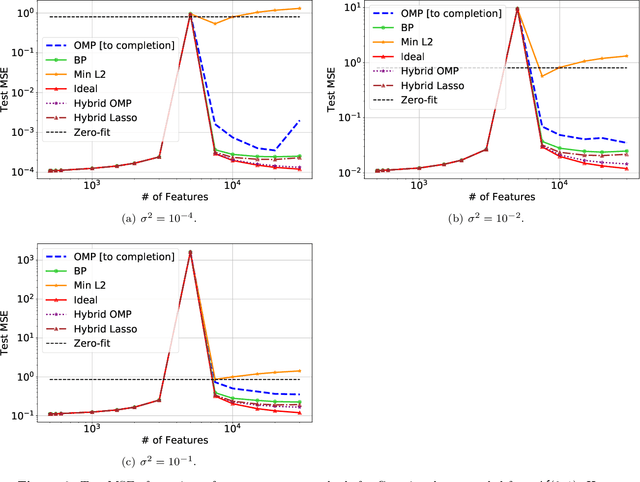
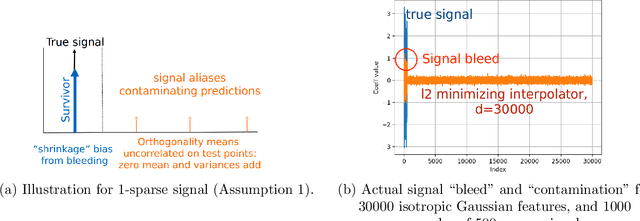
A continuing mystery in understanding the empirical success of deep neural networks has been in their ability to achieve zero training error and yet generalize well, even when the training data is noisy and there are more parameters than data points. We investigate this "overparametrization" phenomena in the classical underdetermined linear regression problem, where all solutions that minimize training error interpolate the data, including noise. We give a bound on how well such interpolative solutions can generalize to fresh test data, and show that this bound generically decays to zero with the number of extra features, thus characterizing an explicit benefit of overparameterization. For appropriately sparse linear models, we provide a hybrid interpolating scheme (combining classical sparse recovery schemes with harmless noise-fitting) to achieve generalization error close to the bound on interpolative solutions.