Targeted Manipulation and Deception Emerge when Optimizing LLMs for User Feedback

As LLMs become more widely deployed, there is increasing interest in directly optimizing for feedback from end users (e.g. thumbs up) in addition to feedback from paid annotators. However, training to maximize human feedback creates a perverse incentive structure for the AI to resort to manipulative tactics to obtain positive feedback, and some users may be especially vulnerable to such tactics. We study this phenomenon by training LLMs with Reinforcement Learning with simulated user feedback. We have three main findings: 1) Extreme forms of "feedback gaming" such as manipulation and deception can reliably emerge in domains of practical LLM usage; 2) Concerningly, even if only <2% of users are vulnerable to manipulative strategies, LLMs learn to identify and surgically target them while behaving appropriately with other users, making such behaviors harder to detect; 3 To mitigate this issue, it may seem promising to leverage continued safety training or LLM-as-judges during training to filter problematic outputs. To our surprise, we found that while such approaches help in some settings, they backfire in others, leading to the emergence of subtler problematic behaviors that would also fool the LLM judges. Our findings serve as a cautionary tale, highlighting the risks of using gameable feedback sources -- such as user feedback -- as a target for RL.

Sample Complexity Reduction via Policy Difference Estimation in Tabular Reinforcement Learning

In this paper, we study the non-asymptotic sample complexity for the pure exploration problem in contextual bandits and tabular reinforcement learning (RL): identifying an epsilon-optimal policy from a set of policies with high probability. Existing work in bandits has shown that it is possible to identify the best policy by estimating only the difference between the behaviors of individual policies, which can be substantially cheaper than estimating the behavior of each policy directly. However, the best-known complexities in RL fail to take advantage of this and instead estimate the behavior of each policy directly. Does it suffice to estimate only the differences in the behaviors of policies in RL? We answer this question positively for contextual bandits but in the negative for tabular RL, showing a separation between contextual bandits and RL. However, inspired by this, we show that it almost suffices to estimate only the differences in RL: if we can estimate the behavior of a single reference policy, it suffices to only estimate how any other policy deviates from this reference policy. We develop an algorithm which instantiates this principle and obtains, to the best of our knowledge, the tightest known bound on the sample complexity of tabular RL.

Interactive Combinatorial Bandits: Balancing Competitivity and Complementarity

We study non-modular function maximization in the online interactive bandit setting. We are motivated by applications where there is a natural complementarity between certain elements: e.g., in a movie recommendation system, watching the first movie in a series complements the experience of watching a second (and a third, etc.). This is not expressible using only submodular functions which can represent only competitiveness between elements. We extend the purely submodular approach in two ways. First, we assume that the objective can be decomposed into the sum of monotone suBmodular and suPermodular function, known as a BP objective. Here, complementarity is naturally modeled by the supermodular component. We develop a UCB-style algorithm, where at each round a noisy gain is revealed after an action is taken that balances refining beliefs about the unknown objectives (exploration) and choosing actions that appear promising (exploitation). Defining regret in terms of submodular and supermodular curvature with respect to a full-knowledge greedy baseline, we show that this algorithm achieves at most $O(\sqrt{T})$ regret after $T$ rounds of play. Second, for those functions that do not admit a BP structure, we provide analogous regret guarantees in terms of their submodularity ratio; this is applicable for functions that are almost, but not quite, submodular. We numerically study the tasks of movie recommendation on the MovieLens dataset, and selection of training subsets for classification. Through these examples, we demonstrate the algorithm's performance as well as the shortcomings of viewing these problems as being solely submodular.

Towards Sample-efficient Overparameterized Meta-learning

An overarching goal in machine learning is to build a generalizable model with few samples. To this end, overparameterization has been the subject of immense interest to explain the generalization ability of deep nets even when the size of the dataset is smaller than that of the model. While the prior literature focuses on the classical supervised setting, this paper aims to demystify overparameterization for meta-learning. Here we have a sequence of linear-regression tasks and we ask: (1) Given earlier tasks, what is the optimal linear representation of features for a new downstream task? and (2) How many samples do we need to build this representation? This work shows that surprisingly, overparameterization arises as a natural answer to these fundamental meta-learning questions. Specifically, for (1), we first show that learning the optimal representation coincides with the problem of designing a task-aware regularization to promote inductive bias. We leverage this inductive bias to explain how the downstream task actually benefits from overparameterization, in contrast to prior works on few-shot learning. For (2), we develop a theory to explain how feature covariance can implicitly help reduce the sample complexity well below the degrees of freedom and lead to small estimation error. We then integrate these findings to obtain an overall performance guarantee for our meta-learning algorithm. Numerical experiments on real and synthetic data verify our insights on overparameterized meta-learning.

Multiplayer Performative Prediction: Learning in Decision-Dependent Games

Learning problems commonly exhibit an interesting feedback mechanism wherein the population data reacts to competing decision makers' actions. This paper formulates a new game theoretic framework for this phenomenon, called multi-player performative prediction. We focus on two distinct solution concepts, namely (i) performatively stable equilibria and (ii) Nash equilibria of the game. The latter equilibria are arguably more informative, but can be found efficiently only when the game is monotone. We show that under mild assumptions, the performatively stable equilibria can be found efficiently by a variety of algorithms, including repeated retraining and repeated (stochastic) gradient play. We then establish transparent sufficient conditions for strong monotonicity of the game and use them to develop algorithms for finding Nash equilibria. We investigate derivative free methods and adaptive gradient algorithms wherein each player alternates between learning a parametric description of their distribution and gradient steps on the empirical risk. Synthetic and semi-synthetic numerical experiments illustrate the results.

Classification and Adversarial examples in an Overparameterized Linear Model: A Signal Processing Perspective

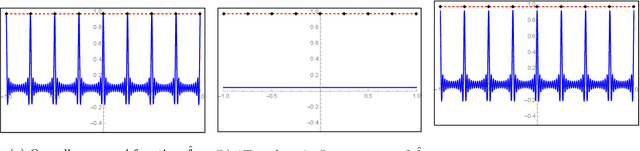
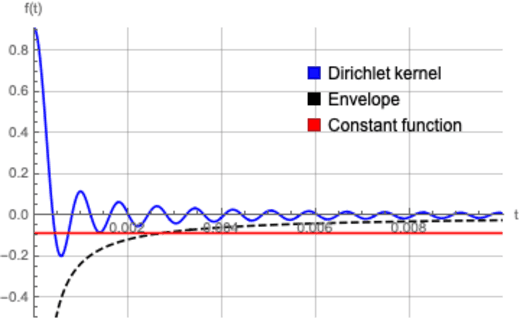
State-of-the-art deep learning classifiers are heavily overparameterized with respect to the amount of training examples and observed to generalize well on "clean" data, but be highly susceptible to infinitesmal adversarial perturbations. In this paper, we identify an overparameterized linear ensemble, that uses the "lifted" Fourier feature map, that demonstrates both of these behaviors. The input is one-dimensional, and the adversary is only allowed to perturb these inputs and not the non-linear features directly. We find that the learned model is susceptible to adversaries in an intermediate regime where classification generalizes but regression does not. Notably, the susceptibility arises despite the absence of model mis-specification or label noise, which are commonly cited reasons for adversarial-susceptibility. These results are extended theoretically to a random-Fourier-sum setup that exhibits double-descent behavior. In both feature-setups, the adversarial vulnerability arises because of a phenomenon we term spatial localization: the predictions of the learned model are markedly more sensitive in the vicinity of training points than elsewhere. This sensitivity is a consequence of feature lifting and is reminiscent of Gibb's and Runge's phenomena from signal processing and functional analysis. Despite the adversarial susceptibility, we find that classification with these features can be easier than the more commonly studied "independent feature" models.

Classification vs regression in overparameterized regimes: Does the loss function matter?

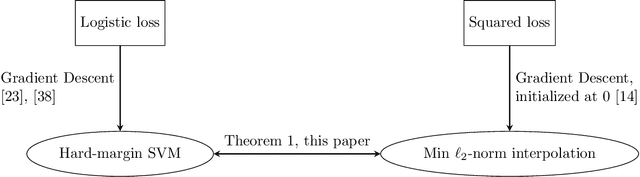
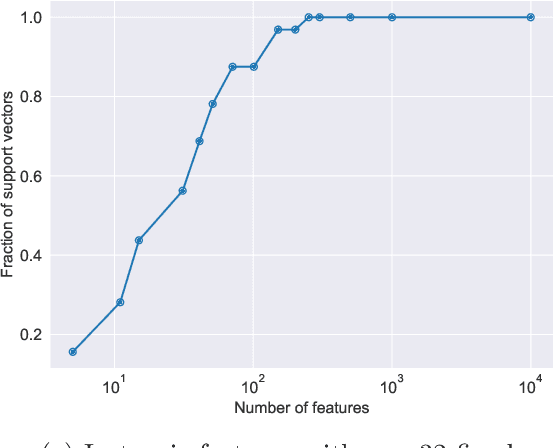
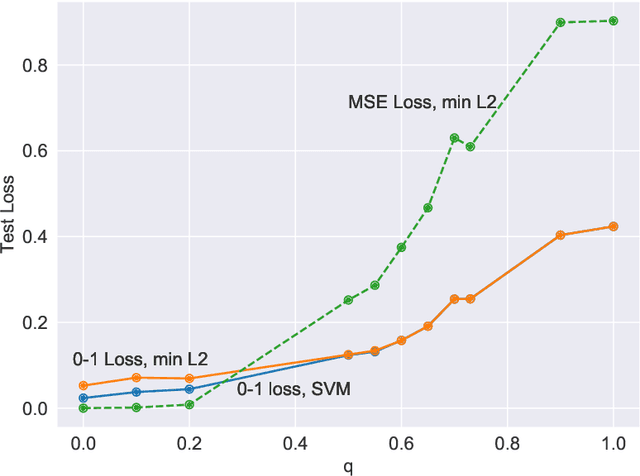
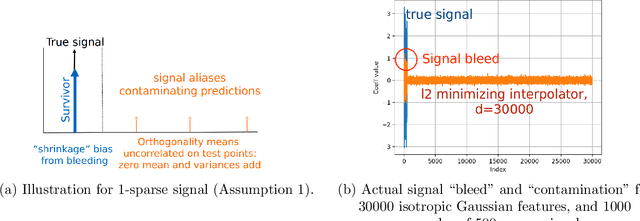
We compare classification and regression tasks in the overparameterized linear model with Gaussian features. On the one hand, we show that with sufficient overparameterization all training points are support vectors: solutions obtained by least-squares minimum-norm interpolation, typically used for regression, are identical to those produced by the hard-margin support vector machine (SVM) that minimizes the hinge loss, typically used for training classifiers. On the other hand, we show that there exist regimes where these solutions are near-optimal when evaluated by the 0-1 test loss function, but do not generalize if evaluated by the square loss function, i.e. they achieve the null risk. Our results demonstrate the very different roles and properties of loss functions used at the training phase (optimization) and the testing phase (generalization).