Active learning of neural population dynamics using two-photon holographic optogenetics

Recent advances in techniques for monitoring and perturbing neural populations have greatly enhanced our ability to study circuits in the brain. In particular, two-photon holographic optogenetics now enables precise photostimulation of experimenter-specified groups of individual neurons, while simultaneous two-photon calcium imaging enables the measurement of ongoing and induced activity across the neural population. Despite the enormous space of potential photostimulation patterns and the time-consuming nature of photostimulation experiments, very little algorithmic work has been done to determine the most effective photostimulation patterns for identifying the neural population dynamics. Here, we develop methods to efficiently select which neurons to stimulate such that the resulting neural responses will best inform a dynamical model of the neural population activity. Using neural population responses to photostimulation in mouse motor cortex, we demonstrate the efficacy of a low-rank linear dynamical systems model, and develop an active learning procedure which takes advantage of low-rank structure to determine informative photostimulation patterns. We demonstrate our approach on both real and synthetic data, obtaining in some cases as much as a two-fold reduction in the amount of data required to reach a given predictive power. Our active stimulation design method is based on a novel active learning procedure for low-rank regression, which may be of independent interest.

Overcoming the Sim-to-Real Gap: Leveraging Simulation to Learn to Explore for Real-World RL

In order to mitigate the sample complexity of real-world reinforcement learning, common practice is to first train a policy in a simulator where samples are cheap, and then deploy this policy in the real world, with the hope that it generalizes effectively. Such \emph{direct sim2real} transfer is not guaranteed to succeed, however, and in cases where it fails, it is unclear how to best utilize the simulator. In this work, we show that in many regimes, while direct sim2real transfer may fail, we can utilize the simulator to learn a set of \emph{exploratory} policies which enable efficient exploration in the real world. In particular, in the setting of low-rank MDPs, we show that coupling these exploratory policies with simple, practical approaches -- least-squares regression oracles and naive randomized exploration -- yields a polynomial sample complexity in the real world, an exponential improvement over direct sim2real transfer, or learning without access to a simulator. To the best of our knowledge, this is the first evidence that simulation transfer yields a provable gain in reinforcement learning in settings where direct sim2real transfer fails. We validate our theoretical results on several realistic robotic simulators and a real-world robotic sim2real task, demonstrating that transferring exploratory policies can yield substantial gains in practice as well.

Corruption-Robust Linear Bandits: Minimax Optimality and Gap-Dependent Misspecification

In linear bandits, how can a learner effectively learn when facing corrupted rewards? While significant work has explored this question, a holistic understanding across different adversarial models and corruption measures is lacking, as is a full characterization of the minimax regret bounds. In this work, we compare two types of corruptions commonly considered: strong corruption, where the corruption level depends on the action chosen by the learner, and weak corruption, where the corruption level does not depend on the action chosen by the learner. We provide a unified framework to analyze these corruptions. For stochastic linear bandits, we fully characterize the gap between the minimax regret under strong and weak corruptions. We also initiate the study of corrupted adversarial linear bandits, obtaining upper and lower bounds with matching dependencies on the corruption level. Next, we reveal a connection between corruption-robust learning and learning with gap-dependent mis-specification, a setting first studied by Liu et al. (2023a), where the misspecification level of an action or policy is proportional to its suboptimality. We present a general reduction that enables any corruption-robust algorithm to handle gap-dependent misspecification. This allows us to recover the results of Liu et al. (2023a) in a black-box manner and significantly generalize them to settings like linear MDPs, yielding the first results for gap-dependent misspecification in reinforcement learning. However, this general reduction does not attain the optimal rate for gap-dependent misspecification. Motivated by this, we develop a specialized algorithm that achieves optimal bounds for gap-dependent misspecification in linear bandits, thus answering an open question posed by Liu et al. (2023a).

Humor in AI: Massive Scale Crowd-Sourced Preferences and Benchmarks for Cartoon Captioning

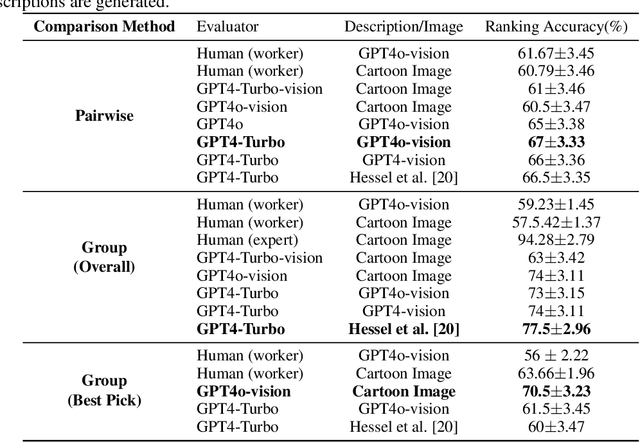
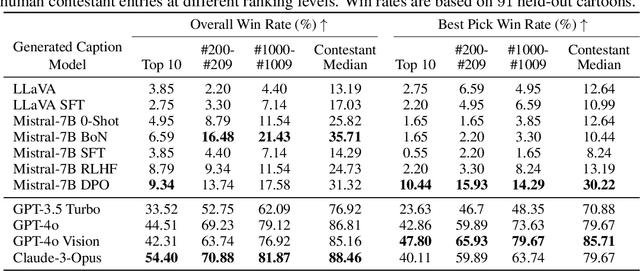
We present a novel multimodal preference dataset for creative tasks, consisting of over 250 million human ratings on more than 2.2 million captions, collected through crowdsourcing rating data for The New Yorker's weekly cartoon caption contest over the past eight years. This unique dataset supports the development and evaluation of multimodal large language models and preference-based fine-tuning algorithms for humorous caption generation. We propose novel benchmarks for judging the quality of model-generated captions, utilizing both GPT4 and human judgments to establish ranking-based evaluation strategies. Our experimental results highlight the limitations of current fine-tuning methods, such as RLHF and DPO, when applied to creative tasks. Furthermore, we demonstrate that even state-of-the-art models like GPT4 and Claude currently underperform top human contestants in generating humorous captions. As we conclude this extensive data collection effort, we release the entire preference dataset to the research community, fostering further advancements in AI humor generation and evaluation.

Sample Complexity Reduction via Policy Difference Estimation in Tabular Reinforcement Learning

In this paper, we study the non-asymptotic sample complexity for the pure exploration problem in contextual bandits and tabular reinforcement learning (RL): identifying an epsilon-optimal policy from a set of policies with high probability. Existing work in bandits has shown that it is possible to identify the best policy by estimating only the difference between the behaviors of individual policies, which can be substantially cheaper than estimating the behavior of each policy directly. However, the best-known complexities in RL fail to take advantage of this and instead estimate the behavior of each policy directly. Does it suffice to estimate only the differences in the behaviors of policies in RL? We answer this question positively for contextual bandits but in the negative for tabular RL, showing a separation between contextual bandits and RL. However, inspired by this, we show that it almost suffices to estimate only the differences in RL: if we can estimate the behavior of a single reference policy, it suffices to only estimate how any other policy deviates from this reference policy. We develop an algorithm which instantiates this principle and obtains, to the best of our knowledge, the tightest known bound on the sample complexity of tabular RL.

ASID: Active Exploration for System Identification in Robotic Manipulation

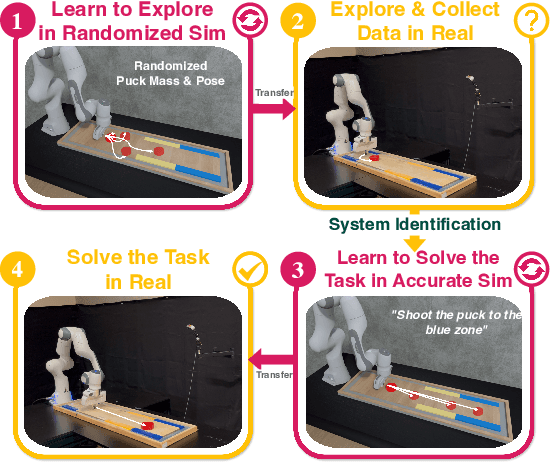
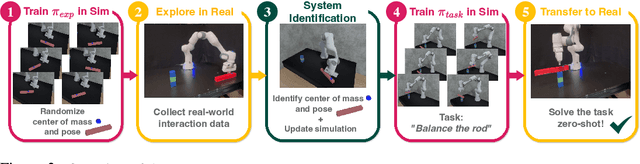
Model-free control strategies such as reinforcement learning have shown the ability to learn control strategies without requiring an accurate model or simulator of the world. While this is appealing due to the lack of modeling requirements, such methods can be sample inefficient, making them impractical in many real-world domains. On the other hand, model-based control techniques leveraging accurate simulators can circumvent these challenges and use a large amount of cheap simulation data to learn controllers that can effectively transfer to the real world. The challenge with such model-based techniques is the requirement for an extremely accurate simulation, requiring both the specification of appropriate simulation assets and physical parameters. This requires considerable human effort to design for every environment being considered. In this work, we propose a learning system that can leverage a small amount of real-world data to autonomously refine a simulation model and then plan an accurate control strategy that can be deployed in the real world. Our approach critically relies on utilizing an initial (possibly inaccurate) simulator to design effective exploration policies that, when deployed in the real world, collect high-quality data. We demonstrate the efficacy of this paradigm in identifying articulation, mass, and other physical parameters in several challenging robotic manipulation tasks, and illustrate that only a small amount of real-world data can allow for effective sim-to-real transfer. Project website at https://weirdlabuw.github.io/asid

Fair Active Learning in Low-Data Regimes

In critical machine learning applications, ensuring fairness is essential to avoid perpetuating social inequities. In this work, we address the challenges of reducing bias and improving accuracy in data-scarce environments, where the cost of collecting labeled data prohibits the use of large, labeled datasets. In such settings, active learning promises to maximize marginal accuracy gains of small amounts of labeled data. However, existing applications of active learning for fairness fail to deliver on this, typically requiring large labeled datasets, or failing to ensure the desired fairness tolerance is met on the population distribution. To address such limitations, we introduce an innovative active learning framework that combines an exploration procedure inspired by posterior sampling with a fair classification subroutine. We demonstrate that this framework performs effectively in very data-scarce regimes, maximizing accuracy while satisfying fairness constraints with high probability. We evaluate our proposed approach using well-established real-world benchmark datasets and compare it against state-of-the-art methods, demonstrating its effectiveness in producing fair models, and improvement over existing methods.

Optimal Exploration for Model-Based RL in Nonlinear Systems

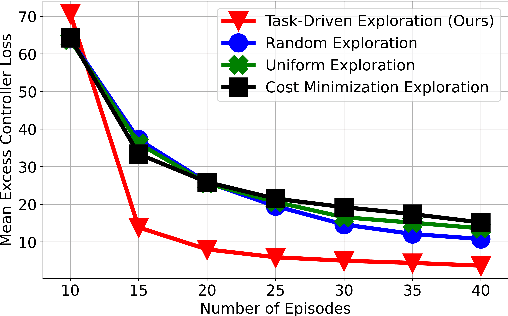
Learning to control unknown nonlinear dynamical systems is a fundamental problem in reinforcement learning and control theory. A commonly applied approach is to first explore the environment (exploration), learn an accurate model of it (system identification), and then compute an optimal controller with the minimum cost on this estimated system (policy optimization). While existing work has shown that it is possible to learn a uniformly good model of the system~\citep{mania2020active}, in practice, if we aim to learn a good controller with a low cost on the actual system, certain system parameters may be significantly more critical than others, and we therefore ought to focus our exploration on learning such parameters. In this work, we consider the setting of nonlinear dynamical systems and seek to formally quantify, in such settings, (a) which parameters are most relevant to learning a good controller, and (b) how we can best explore so as to minimize uncertainty in such parameters. Inspired by recent work in linear systems~\citep{wagenmaker2021task}, we show that minimizing the controller loss in nonlinear systems translates to estimating the system parameters in a particular, task-dependent metric. Motivated by this, we develop an algorithm able to efficiently explore the system to reduce uncertainty in this metric, and prove a lower bound showing that our approach learns a controller at a near-instance-optimal rate. Our algorithm relies on a general reduction from policy optimization to optimal experiment design in arbitrary systems, and may be of independent interest. We conclude with experiments demonstrating the effectiveness of our method in realistic nonlinear robotic systems.

Instance-Optimality in Interactive Decision Making: Toward a Non-Asymptotic Theory

We consider the development of adaptive, instance-dependent algorithms for interactive decision making (bandits, reinforcement learning, and beyond) that, rather than only performing well in the worst case, adapt to favorable properties of real-world instances for improved performance. We aim for instance-optimality, a strong notion of adaptivity which asserts that, on any particular problem instance, the algorithm under consideration outperforms all consistent algorithms. Instance-optimality enjoys a rich asymptotic theory originating from the work of \citet{lai1985asymptotically,graves1997asymptotically}, but non-asymptotic guarantees have remained elusive outside of certain special cases. Even for problems as simple as tabular reinforcement learning, existing algorithms do not attain instance-optimal performance until the number of rounds of interaction is doubly exponential in the number of states. In this paper, we take the first step toward developing a non-asymptotic theory of instance-optimal decision making with general function approximation. We introduce a new complexity measure, the Allocation-Estimation Coefficient (AEC), and provide a new algorithm, $\mathsf{AE}^2$, which attains non-asymptotic instance-optimal performance at a rate controlled by the AEC. Our results recover the best known guarantees for well-studied problems such as finite-armed and linear bandits and, when specialized to tabular reinforcement learning, attain the first instance-optimal regret bounds with polynomial dependence on all problem parameters, improving over prior work exponentially. We complement these results with lower bounds that show that i) existing notions of statistical complexity are insufficient to derive non-asymptotic guarantees, and ii) under certain technical conditions, boundedness of the AEC is necessary to learn an instance-optimal allocation of decisions in finite time.

Leveraging Offline Data in Online Reinforcement Learning

Two central paradigms have emerged in the reinforcement learning (RL) community: online RL and offline RL. In the online RL setting, the agent has no prior knowledge of the environment, and must interact with it in order to find an $\epsilon$-optimal policy. In the offline RL setting, the learner instead has access to a fixed dataset to learn from, but is unable to otherwise interact with the environment, and must obtain the best policy it can from this offline data. Practical scenarios often motivate an intermediate setting: if we have some set of offline data and, in addition, may also interact with the environment, how can we best use the offline data to minimize the number of online interactions necessary to learn an $\epsilon$-optimal policy? In this work, we consider this setting, which we call the \textsf{FineTuneRL} setting, for MDPs with linear structure. We characterize the necessary number of online samples needed in this setting given access to some offline dataset, and develop an algorithm, \textsc{FTPedel}, which is provably optimal. We show through an explicit example that combining offline data with online interactions can lead to a provable improvement over either purely offline or purely online RL. Finally, our results illustrate the distinction between \emph{verifiable} learning, the typical setting considered in online RL, and \emph{unverifiable} learning, the setting often considered in offline RL, and show that there is a formal separation between these regimes.