Humor in AI: Massive Scale Crowd-Sourced Preferences and Benchmarks for Cartoon Captioning

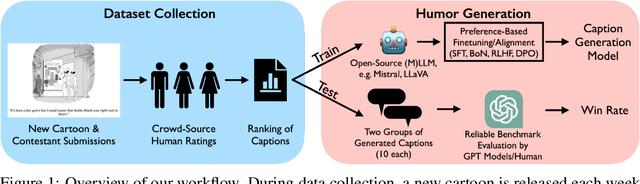
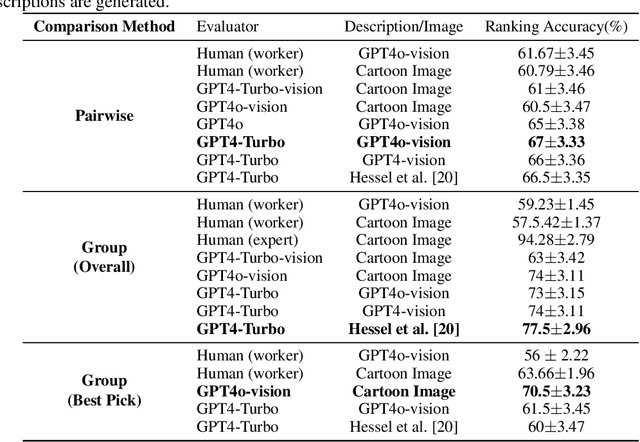
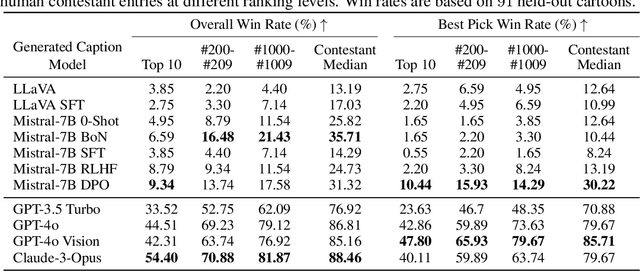
We present a novel multimodal preference dataset for creative tasks, consisting of over 250 million human ratings on more than 2.2 million captions, collected through crowdsourcing rating data for The New Yorker's weekly cartoon caption contest over the past eight years. This unique dataset supports the development and evaluation of multimodal large language models and preference-based fine-tuning algorithms for humorous caption generation. We propose novel benchmarks for judging the quality of model-generated captions, utilizing both GPT4 and human judgments to establish ranking-based evaluation strategies. Our experimental results highlight the limitations of current fine-tuning methods, such as RLHF and DPO, when applied to creative tasks. Furthermore, we demonstrate that even state-of-the-art models like GPT4 and Claude currently underperform top human contestants in generating humorous captions. As we conclude this extensive data collection effort, we release the entire preference dataset to the research community, fostering further advancements in AI humor generation and evaluation.

Improving the convergence of SGD through adaptive batch sizes

Mini-batch stochastic gradient descent (SGD) approximates the gradient of an objective function with the average gradient of some batch of constant size. While small batch sizes can yield high-variance gradient estimates that prevent the model from learning a good model, large batches may require more data and computational effort. This work presents a method to change the batch size adaptively with model quality. We show that our method requires the same number of model updates as full-batch gradient descent while requiring the same total number of gradient computations as SGD. While this method requires evaluating the objective function, we present a passive approximation that eliminates this constraint and improves computational efficiency. We provide extensive experiments illustrating that our methods require far fewer model updates without increasing the total amount of computation.

ATOMO: Communication-efficient Learning via Atomic Sparsification

Distributed model training suffers from communication overheads due to frequent gradient updates transmitted between compute nodes. To mitigate these overheads, several studies propose the use of sparsified stochastic gradients. We argue that these are facets of a general sparsification method that can operate on any possible atomic decomposition. Notable examples include element-wise, singular value, and Fourier decompositions. We present ATOMO, a general framework for atomic sparsification of stochastic gradients. Given a gradient, an atomic decomposition, and a sparsity budget, ATOMO gives a random unbiased sparsification of the atoms minimizing variance. We show that methods such as QSGD and TernGrad are special cases of ATOMO and show that sparsifiying gradients in their singular value decomposition (SVD), rather than the coordinate-wise one, can lead to significantly faster distributed training.