Accelerating Scientific Research with Gemini: Case Studies and Common Techniques

Recent advances in large language models (LLMs) have opened new avenues for accelerating scientific research. While models are increasingly capable of assisting with routine tasks, their ability to contribute to novel, expert-level mathematical discovery is less understood. We present a collection of case studies demonstrating how researchers have successfully collaborated with advanced AI models, specifically Google's Gemini-based models (in particular Gemini Deep Think and its advanced variants), to solve open problems, refute conjectures, and generate new proofs across diverse areas in theoretical computer science, as well as other areas such as economics, optimization, and physics. Based on these experiences, we extract common techniques for effective human-AI collaboration in theoretical research, such as iterative refinement, problem decomposition, and cross-disciplinary knowledge transfer. While the majority of our results stem from this interactive, conversational methodology, we also highlight specific instances that push beyond standard chat interfaces. These include deploying the model as a rigorous adversarial reviewer to detect subtle flaws in existing proofs, and embedding it within a "neuro-symbolic" loop that autonomously writes and executes code to verify complex derivations. Together, these examples highlight the potential of AI not just as a tool for automation, but as a versatile, genuine partner in the creative process of scientific discovery.

Gradients can train reward models: An Empirical Risk Minimization Approach for Offline Inverse RL and Dynamic Discrete Choice Model

We study the problem of estimating Dynamic Discrete Choice (DDC) models, also known as offline Maximum Entropy-Regularized Inverse Reinforcement Learning (offline MaxEnt-IRL) in machine learning. The objective is to recover reward or $Q^*$ functions that govern agent behavior from offline behavior data. In this paper, we propose a globally convergent gradient-based method for solving these problems without the restrictive assumption of linearly parameterized rewards. The novelty of our approach lies in introducing the Empirical Risk Minimization (ERM) based IRL/DDC framework, which circumvents the need for explicit state transition probability estimation in the Bellman equation. Furthermore, our method is compatible with non-parametric estimation techniques such as neural networks. Therefore, the proposed method has the potential to be scaled to high-dimensional, infinite state spaces. A key theoretical insight underlying our approach is that the Bellman residual satisfies the Polyak-Lojasiewicz (PL) condition -- a property that, while weaker than strong convexity, is sufficient to ensure fast global convergence guarantees. Through a series of synthetic experiments, we demonstrate that our approach consistently outperforms benchmark methods and state-of-the-art alternatives.

Humor in AI: Massive Scale Crowd-Sourced Preferences and Benchmarks for Cartoon Captioning

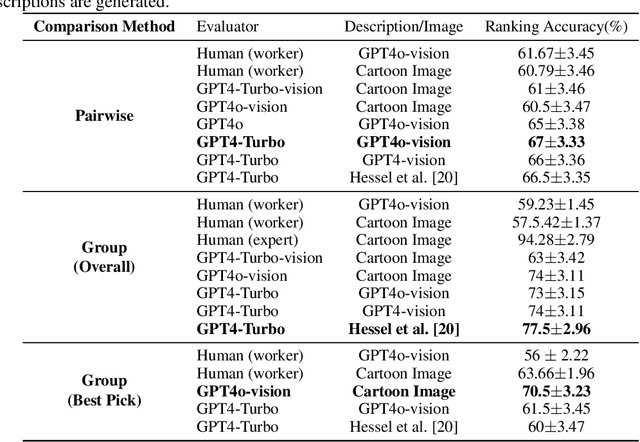
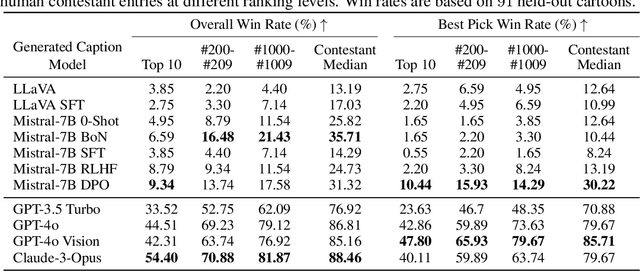
We present a novel multimodal preference dataset for creative tasks, consisting of over 250 million human ratings on more than 2.2 million captions, collected through crowdsourcing rating data for The New Yorker's weekly cartoon caption contest over the past eight years. This unique dataset supports the development and evaluation of multimodal large language models and preference-based fine-tuning algorithms for humorous caption generation. We propose novel benchmarks for judging the quality of model-generated captions, utilizing both GPT4 and human judgments to establish ranking-based evaluation strategies. Our experimental results highlight the limitations of current fine-tuning methods, such as RLHF and DPO, when applied to creative tasks. Furthermore, we demonstrate that even state-of-the-art models like GPT4 and Claude currently underperform top human contestants in generating humorous captions. As we conclude this extensive data collection effort, we release the entire preference dataset to the research community, fostering further advancements in AI humor generation and evaluation.

Adaptive Experimentation When You Can't Experiment

This paper introduces the \emph{confounded pure exploration transductive linear bandit} (\texttt{CPET-LB}) problem. As a motivating example, often online services cannot directly assign users to specific control or treatment experiences either for business or practical reasons. In these settings, naively comparing treatment and control groups that may result from self-selection can lead to biased estimates of underlying treatment effects. Instead, online services can employ a properly randomized encouragement that incentivizes users toward a specific treatment. Our methodology provides online services with an adaptive experimental design approach for learning the best-performing treatment for such \textit{encouragement designs}. We consider a more general underlying model captured by a linear structural equation and formulate pure exploration linear bandits in this setting. Though pure exploration has been extensively studied in standard adaptive experimental design settings, we believe this is the first work considering a setting where noise is confounded. Elimination-style algorithms using experimental design methods in combination with a novel finite-time confidence interval on an instrumental variable style estimator are presented with sample complexity upper bounds nearly matching a minimax lower bound. Finally, experiments are conducted that demonstrate the efficacy of our approach.

Off-Policy Evaluation from Logged Human Feedback

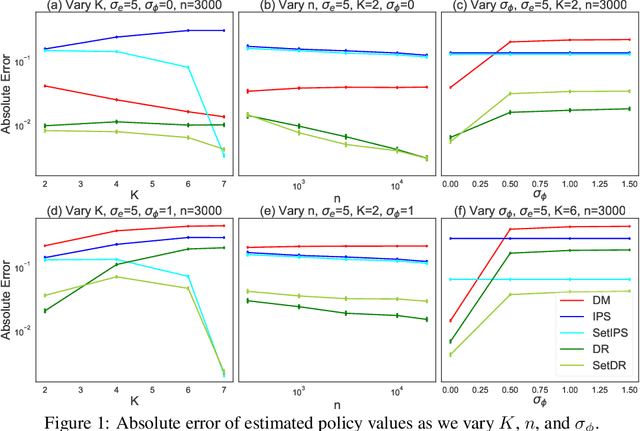
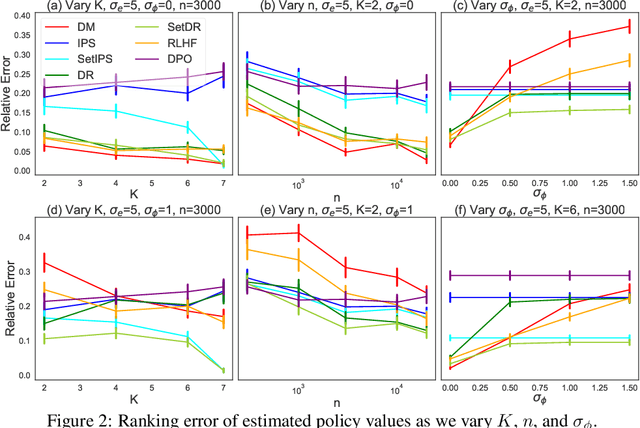
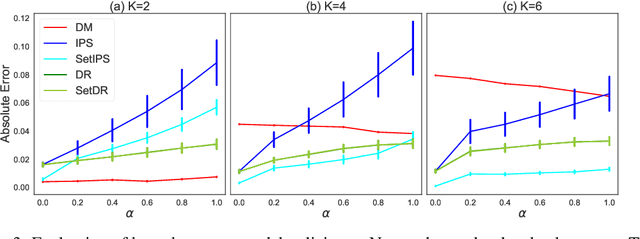
Learning from human feedback has been central to recent advances in artificial intelligence and machine learning. Since the collection of human feedback is costly, a natural question to ask is if the new feedback always needs to collected. Or could we evaluate a new model with the human feedback on responses of another model? This motivates us to study off-policy evaluation from logged human feedback. We formalize the problem, propose both model-based and model-free estimators for policy values, and show how to optimize them. We analyze unbiasedness of our estimators and evaluate them empirically. Our estimators can predict the absolute values of evaluated policies, rank them, and be optimized.

Best of Three Worlds: Adaptive Experimentation for Digital Marketing in Practice

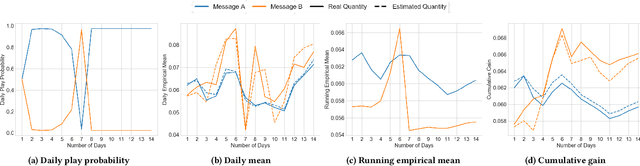
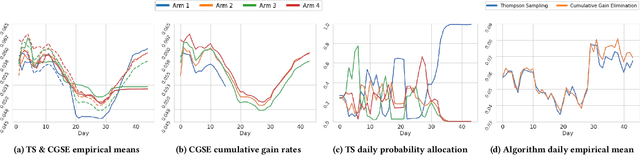
Adaptive experimental design (AED) methods are increasingly being used in industry as a tool to boost testing throughput or reduce experimentation cost relative to traditional A/B/N testing methods. However, the behavior and guarantees of such methods are not well-understood beyond idealized stationary settings. This paper shares lessons learned regarding the challenges of naively using AED systems in industrial settings where non-stationarity is prevalent, while also providing perspectives on the proper objectives and system specifications in such settings. We developed an AED framework for counterfactual inference based on these experiences, and tested it in a commercial environment.

DIRECT: Deep Active Learning under Imbalance and Label Noise

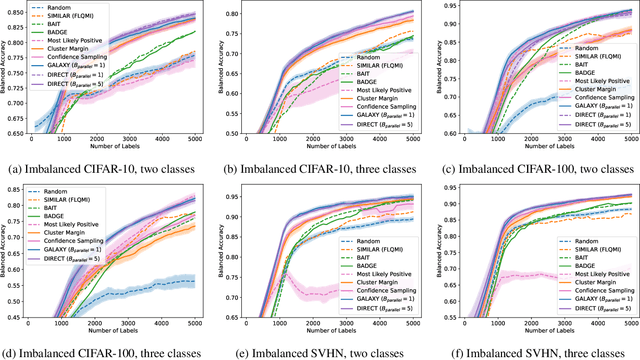
Class imbalance is a prevalent issue in real world machine learning applications, often leading to poor performance in rare and minority classes. With an abundance of wild unlabeled data, active learning is perhaps the most effective technique in solving the problem at its root -- collecting a more balanced and informative set of labeled examples during annotation. In this work, we propose a novel algorithm that first identifies the class separation threshold and then annotate the most uncertain examples from the minority classes, close to the separation threshold. Through a novel reduction to one-dimensional active learning, our algorithm DIRECT is able to leverage the classic active learning literature to address issues such as batch labeling and tolerance towards label noise. Compared to existing algorithms, our algorithm saves more than 15\% of the annotation budget compared to state-of-art active learning algorithm and more than 90\% of annotation budget compared to random sampling.

Fair Active Learning in Low-Data Regimes

In critical machine learning applications, ensuring fairness is essential to avoid perpetuating social inequities. In this work, we address the challenges of reducing bias and improving accuracy in data-scarce environments, where the cost of collecting labeled data prohibits the use of large, labeled datasets. In such settings, active learning promises to maximize marginal accuracy gains of small amounts of labeled data. However, existing applications of active learning for fairness fail to deliver on this, typically requiring large labeled datasets, or failing to ensure the desired fairness tolerance is met on the population distribution. To address such limitations, we introduce an innovative active learning framework that combines an exploration procedure inspired by posterior sampling with a fair classification subroutine. We demonstrate that this framework performs effectively in very data-scarce regimes, maximizing accuracy while satisfying fairness constraints with high probability. We evaluate our proposed approach using well-established real-world benchmark datasets and compare it against state-of-the-art methods, demonstrating its effectiveness in producing fair models, and improvement over existing methods.

Pessimistic Off-Policy Multi-Objective Optimization

Multi-objective optimization is a type of decision making problems where multiple conflicting objectives are optimized. We study offline optimization of multi-objective policies from data collected by an existing policy. We propose a pessimistic estimator for the multi-objective policy values that can be easily plugged into existing formulas for hypervolume computation and optimized. The estimator is based on inverse propensity scores (IPS), and improves upon a naive IPS estimator in both theory and experiments. Our analysis is general, and applies beyond our IPS estimators and methods for optimizing them. The pessimistic estimator can be optimized by policy gradients and performs well in all of our experiments.

Minimax Optimal Submodular Optimization with Bandit Feedback

We consider maximizing a monotonic, submodular set function $f: 2^{[n]} \rightarrow [0,1]$ under stochastic bandit feedback. Specifically, $f$ is unknown to the learner but at each time $t=1,\dots,T$ the learner chooses a set $S_t \subset [n]$ with $|S_t| \leq k$ and receives reward $f(S_t) + \eta_t$ where $\eta_t$ is mean-zero sub-Gaussian noise. The objective is to minimize the learner's regret over $T$ times with respect to ($1-e^{-1}$)-approximation of maximum $f(S_*)$ with $|S_*| = k$, obtained through greedy maximization of $f$. To date, the best regret bound in the literature scales as $k n^{1/3} T^{2/3}$. And by trivially treating every set as a unique arm one deduces that $\sqrt{ {n \choose k} T }$ is also achievable. In this work, we establish the first minimax lower bound for this setting that scales like $\mathcal{O}(\min_{i \le k}(in^{1/3}T^{2/3} + \sqrt{n^{k-i}T}))$. Moreover, we propose an algorithm that is capable of matching the lower bound regret.