Fair Active Learning in Low-Data Regimes

In critical machine learning applications, ensuring fairness is essential to avoid perpetuating social inequities. In this work, we address the challenges of reducing bias and improving accuracy in data-scarce environments, where the cost of collecting labeled data prohibits the use of large, labeled datasets. In such settings, active learning promises to maximize marginal accuracy gains of small amounts of labeled data. However, existing applications of active learning for fairness fail to deliver on this, typically requiring large labeled datasets, or failing to ensure the desired fairness tolerance is met on the population distribution. To address such limitations, we introduce an innovative active learning framework that combines an exploration procedure inspired by posterior sampling with a fair classification subroutine. We demonstrate that this framework performs effectively in very data-scarce regimes, maximizing accuracy while satisfying fairness constraints with high probability. We evaluate our proposed approach using well-established real-world benchmark datasets and compare it against state-of-the-art methods, demonstrating its effectiveness in producing fair models, and improvement over existing methods.

A/B Testing and Best-arm Identification for Linear Bandits with Robustness to Non-stationarity

We investigate the fixed-budget best-arm identification (BAI) problem for linear bandits in a potentially non-stationary environment. Given a finite arm set $\mathcal{X}\subset\mathbb{R}^d$, a fixed budget $T$, and an unpredictable sequence of parameters $\left\lbrace\theta_t\right\rbrace_{t=1}^{T}$, an algorithm will aim to correctly identify the best arm $x^* := \arg\max_{x\in\mathcal{X}}x^\top\sum_{t=1}^{T}\theta_t$ with probability as high as possible. Prior work has addressed the stationary setting where $\theta_t = \theta_1$ for all $t$ and demonstrated that the error probability decreases as $\exp(-T /\rho^*)$ for a problem-dependent constant $\rho^*$. But in many real-world $A/B/n$ multivariate testing scenarios that motivate our work, the environment is non-stationary and an algorithm expecting a stationary setting can easily fail. For robust identification, it is well-known that if arms are chosen randomly and non-adaptively from a G-optimal design over $\mathcal{X}$ at each time then the error probability decreases as $\exp(-T\Delta^2_{(1)}/d)$, where $\Delta_{(1)} = \min_{x \neq x^*} (x^* - x)^\top \frac{1}{T}\sum_{t=1}^T \theta_t$. As there exist environments where $\Delta_{(1)}^2/ d \ll 1/ \rho^*$, we are motivated to propose a novel algorithm $\mathsf{P1}$-$\mathsf{RAGE}$ that aims to obtain the best of both worlds: robustness to non-stationarity and fast rates of identification in benign settings. We characterize the error probability of $\mathsf{P1}$-$\mathsf{RAGE}$ and demonstrate empirically that the algorithm indeed never performs worse than G-optimal design but compares favorably to the best algorithms in the stationary setting.

Active Learning with Safety Constraints

Active learning methods have shown great promise in reducing the number of samples necessary for learning. As automated learning systems are adopted into real-time, real-world decision-making pipelines, it is increasingly important that such algorithms are designed with safety in mind. In this work we investigate the complexity of learning the best safe decision in interactive environments. We reduce this problem to a constrained linear bandits problem, where our goal is to find the best arm satisfying certain (unknown) safety constraints. We propose an adaptive experimental design-based algorithm, which we show efficiently trades off between the difficulty of showing an arm is unsafe vs suboptimal. To our knowledge, our results are the first on best-arm identification in linear bandits with safety constraints. In practice, we demonstrate that this approach performs well on synthetic and real world datasets.

Nearly Optimal Algorithms for Level Set Estimation

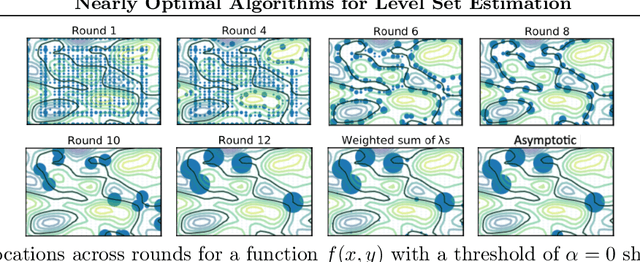
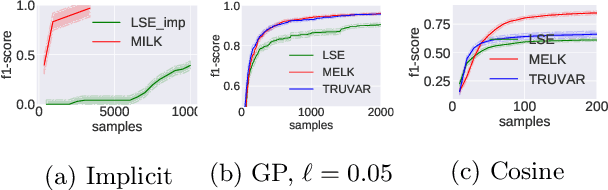
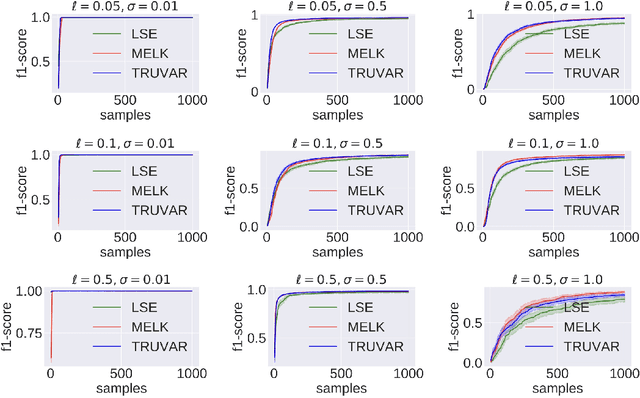
The level set estimation problem seeks to find all points in a domain ${\cal X}$ where the value of an unknown function $f:{\cal X}\rightarrow \mathbb{R}$ exceeds a threshold $\alpha$. The estimation is based on noisy function evaluations that may be acquired at sequentially and adaptively chosen locations in ${\cal X}$. The threshold value $\alpha$ can either be \emph{explicit} and provided a priori, or \emph{implicit} and defined relative to the optimal function value, i.e. $\alpha = (1-\epsilon)f(x_\ast)$ for a given $\epsilon > 0$ where $f(x_\ast)$ is the maximal function value and is unknown. In this work we provide a new approach to the level set estimation problem by relating it to recent adaptive experimental design methods for linear bandits in the Reproducing Kernel Hilbert Space (RKHS) setting. We assume that $f$ can be approximated by a function in the RKHS up to an unknown misspecification and provide novel algorithms for both the implicit and explicit cases in this setting with strong theoretical guarantees. Moreover, in the linear (kernel) setting, we show that our bounds are nearly optimal, namely, our upper bounds match existing lower bounds for threshold linear bandits. To our knowledge this work provides the first instance-dependent, non-asymptotic upper bounds on sample complexity of level-set estimation that match information theoretic lower bounds.

Selective Sampling for Online Best-arm Identification

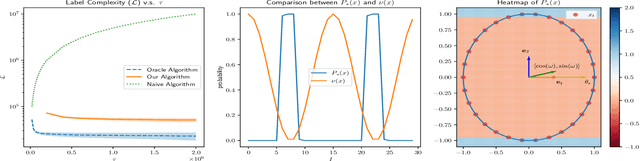
This work considers the problem of selective-sampling for best-arm identification. Given a set of potential options $\mathcal{Z}\subset\mathbb{R}^d$, a learner aims to compute with probability greater than $1-\delta$, $\arg\max_{z\in \mathcal{Z}} z^{\top}\theta_{\ast}$ where $\theta_{\ast}$ is unknown. At each time step, a potential measurement $x_t\in \mathcal{X}\subset\mathbb{R}^d$ is drawn IID and the learner can either choose to take the measurement, in which case they observe a noisy measurement of $x^{\top}\theta_{\ast}$, or to abstain from taking the measurement and wait for a potentially more informative point to arrive in the stream. Hence the learner faces a fundamental trade-off between the number of labeled samples they take and when they have collected enough evidence to declare the best arm and stop sampling. The main results of this work precisely characterize this trade-off between labeled samples and stopping time and provide an algorithm that nearly-optimally achieves the minimal label complexity given a desired stopping time. In addition, we show that the optimal decision rule has a simple geometric form based on deciding whether a point is in an ellipse or not. Finally, our framework is general enough to capture binary classification improving upon previous works.

High-Dimensional Experimental Design and Kernel Bandits

In recent years methods from optimal linear experimental design have been leveraged to obtain state of the art results for linear bandits. A design returned from an objective such as $G$-optimal design is actually a probability distribution over a pool of potential measurement vectors. Consequently, one nuisance of the approach is the task of converting this continuous probability distribution into a discrete assignment of $N$ measurements. While sophisticated rounding techniques have been proposed, in $d$ dimensions they require $N$ to be at least $d$, $d \log(\log(d))$, or $d^2$ based on the sub-optimality of the solution. In this paper we are interested in settings where $N$ may be much less than $d$, such as in experimental design in an RKHS where $d$ may be effectively infinite. In this work, we propose a rounding procedure that frees $N$ of any dependence on the dimension $d$, while achieving nearly the same performance guarantees of existing rounding procedures. We evaluate the procedure against a baseline that projects the problem to a lower dimensional space and performs rounding which requires $N$ to just be at least a notion of the effective dimension. We also leverage our new approach in a new algorithm for kernelized bandits to obtain state of the art results for regret minimization and pure exploration. An advantage of our approach over existing UCB-like approaches is that our kernel bandit algorithms are also robust to model misspecification.