Active learning of neural population dynamics using two-photon holographic optogenetics

Recent advances in techniques for monitoring and perturbing neural populations have greatly enhanced our ability to study circuits in the brain. In particular, two-photon holographic optogenetics now enables precise photostimulation of experimenter-specified groups of individual neurons, while simultaneous two-photon calcium imaging enables the measurement of ongoing and induced activity across the neural population. Despite the enormous space of potential photostimulation patterns and the time-consuming nature of photostimulation experiments, very little algorithmic work has been done to determine the most effective photostimulation patterns for identifying the neural population dynamics. Here, we develop methods to efficiently select which neurons to stimulate such that the resulting neural responses will best inform a dynamical model of the neural population activity. Using neural population responses to photostimulation in mouse motor cortex, we demonstrate the efficacy of a low-rank linear dynamical systems model, and develop an active learning procedure which takes advantage of low-rank structure to determine informative photostimulation patterns. We demonstrate our approach on both real and synthetic data, obtaining in some cases as much as a two-fold reduction in the amount of data required to reach a given predictive power. Our active stimulation design method is based on a novel active learning procedure for low-rank regression, which may be of independent interest.

Universality and individuality in neural dynamics across large populations of recurrent networks

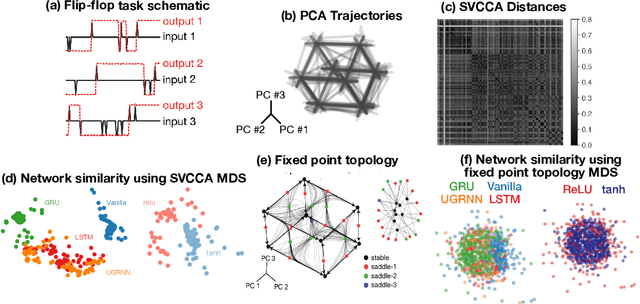
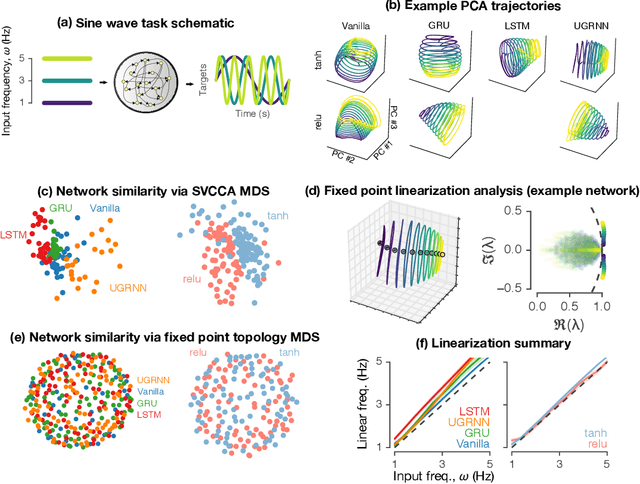
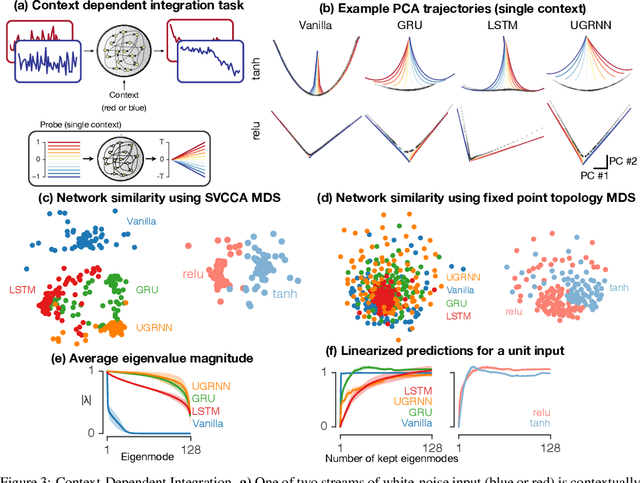
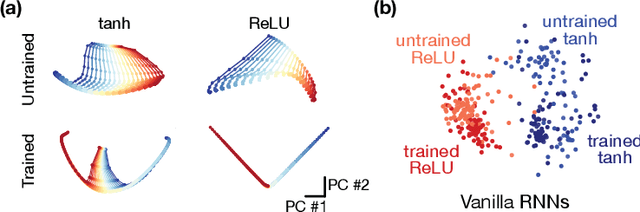
Task-based modeling with recurrent neural networks (RNNs) has emerged as a popular way to infer the computational function of different brain regions. These models are quantitatively assessed by comparing the low-dimensional neural representations of the model with the brain, for example using canonical correlation analysis (CCA). However, the nature of the detailed neurobiological inferences one can draw from such efforts remains elusive. For example, to what extent does training neural networks to solve common tasks uniquely determine the network dynamics, independent of modeling architectural choices? Or alternatively, are the learned dynamics highly sensitive to different model choices? Knowing the answer to these questions has strong implications for whether and how we should use task-based RNN modeling to understand brain dynamics. To address these foundational questions, we study populations of thousands of networks, with commonly used RNN architectures, trained to solve neuroscientifically motivated tasks and characterize their nonlinear dynamics. We find the geometry of the RNN representations can be highly sensitive to different network architectures, yielding a cautionary tale for measures of similarity that rely representational geometry, such as CCA. Moreover, we find that while the geometry of neural dynamics can vary greatly across architectures, the underlying computational scaffold---the topological structure of fixed points, transitions between them, limit cycles, and linearized dynamics---often appears universal across all architectures.

Reverse engineering recurrent networks for sentiment classification reveals line attractor dynamics

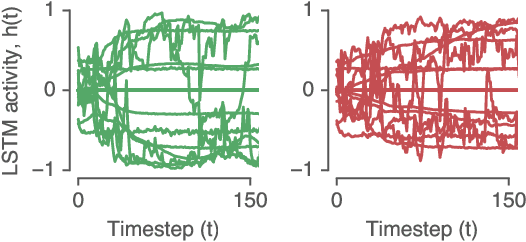
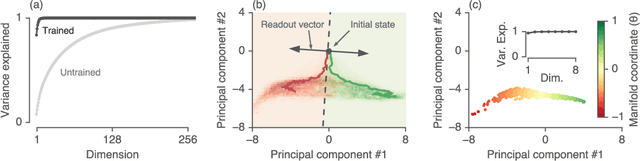
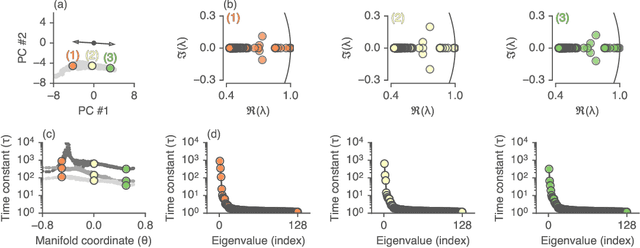
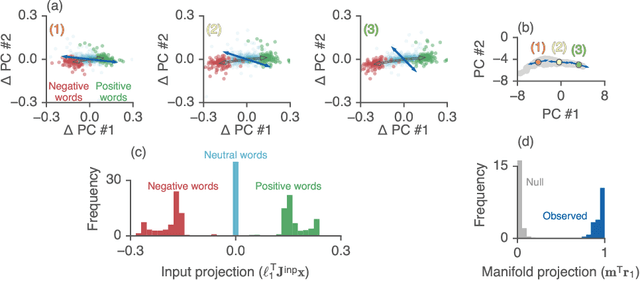
Recurrent neural networks (RNNs) are a widely used tool for modeling sequential data, yet they are often treated as inscrutable black boxes. Given a trained recurrent network, we would like to reverse engineer it--to obtain a quantitative, interpretable description of how it solves a particular task. Even for simple tasks, a detailed understanding of how recurrent networks work, or a prescription for how to develop such an understanding, remains elusive. In this work, we use tools from dynamical systems analysis to reverse engineer recurrent networks trained to perform sentiment classification, a foundational natural language processing task. Given a trained network, we find fixed points of the recurrent dynamics and linearize the nonlinear system around these fixed points. Despite their theoretical capacity to implement complex, high-dimensional computations, we find that trained networks converge to highly interpretable, low-dimensional representations. In particular, the topological structure of the fixed points and corresponding linearized dynamics reveal an approximate line attractor within the RNN, which we can use to quantitatively understand how the RNN solves the sentiment analysis task. Finally, we find this mechanism present across RNN architectures (including LSTMs, GRUs, and vanilla RNNs) trained on multiple datasets, suggesting that our findings are not unique to a particular architecture or dataset. Overall, these results demonstrate that surprisingly universal and human interpretable computations can arise across a range of recurrent networks.