Optimal Exploration for Model-Based RL in Nonlinear Systems
Paper and Code
Jun 15, 2023

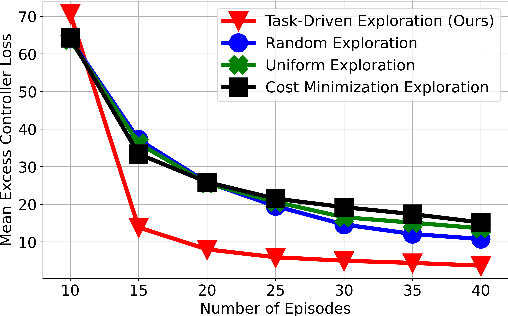

Learning to control unknown nonlinear dynamical systems is a fundamental problem in reinforcement learning and control theory. A commonly applied approach is to first explore the environment (exploration), learn an accurate model of it (system identification), and then compute an optimal controller with the minimum cost on this estimated system (policy optimization). While existing work has shown that it is possible to learn a uniformly good model of the system~\citep{mania2020active}, in practice, if we aim to learn a good controller with a low cost on the actual system, certain system parameters may be significantly more critical than others, and we therefore ought to focus our exploration on learning such parameters. In this work, we consider the setting of nonlinear dynamical systems and seek to formally quantify, in such settings, (a) which parameters are most relevant to learning a good controller, and (b) how we can best explore so as to minimize uncertainty in such parameters. Inspired by recent work in linear systems~\citep{wagenmaker2021task}, we show that minimizing the controller loss in nonlinear systems translates to estimating the system parameters in a particular, task-dependent metric. Motivated by this, we develop an algorithm able to efficiently explore the system to reduce uncertainty in this metric, and prove a lower bound showing that our approach learns a controller at a near-instance-optimal rate. Our algorithm relies on a general reduction from policy optimization to optimal experiment design in arbitrary systems, and may be of independent interest. We conclude with experiments demonstrating the effectiveness of our method in realistic nonlinear robotic systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge