Restricted Spectral Gap Decomposition for Simulated Tempering Targeting Mixture Distributions

Simulated tempering is a widely used strategy for sampling from multimodal distributions. In this paper, we consider simulated tempering combined with an arbitrary local Markov chain Monte Carlo sampler and present a new decomposition theorem that provides a lower bound on the restricted spectral gap of the algorithm for sampling from mixture distributions. By working with the restricted spectral gap, the applicability of our results is extended to broader settings such as when the usual spectral gap is difficult to bound or becomes degenerate. We demonstrate the application of our theoretical results by analyzing simulated tempering combined with random walk Metropolis--Hastings for sampling from mixtures of Gaussian distributions. We show that in fixed-dimensional settings, the algorithm's complexity scales polynomially with the separation between modes and logarithmically with $1/\varepsilon$, where $\varepsilon$ is the target accuracy in total variation distance.

Online Covariance Estimation in Nonsmooth Stochastic Approximation

We consider applying stochastic approximation (SA) methods to solve nonsmooth variational inclusion problems. Existing studies have shown that the averaged iterates of SA methods exhibit asymptotic normality, with an optimal limiting covariance matrix in the local minimax sense of H\'ajek and Le Cam. However, no methods have been proposed to estimate this covariance matrix in a nonsmooth and potentially non-monotone (nonconvex) setting. In this paper, we study an online batch-means covariance matrix estimator introduced in Zhu et al.(2023). The estimator groups the SA iterates appropriately and computes the sample covariance among batches as an estimate of the limiting covariance. Its construction does not require prior knowledge of the total sample size, and updates can be performed recursively as new data arrives. We establish that, as long as the batch size sequence is properly specified (depending on the stepsize sequence), the estimator achieves a convergence rate of order $O(\sqrt{d}n^{-1/8+\varepsilon})$ for any $\varepsilon>0$, where $d$ and $n$ denote the problem dimensionality and the number of iterations (or samples) used. Although the problem is nonsmooth and potentially non-monotone (nonconvex), our convergence rate matches the best-known rate for covariance estimation methods using only first-order information in smooth and strongly-convex settings. The consistency of this covariance estimator enables asymptotically valid statistical inference, including constructing confidence intervals and performing hypothesis testing.

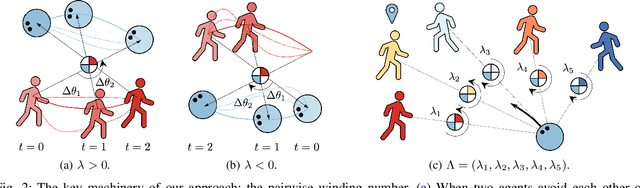
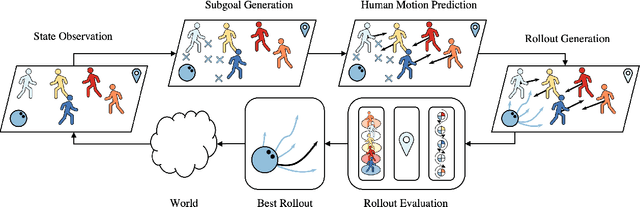
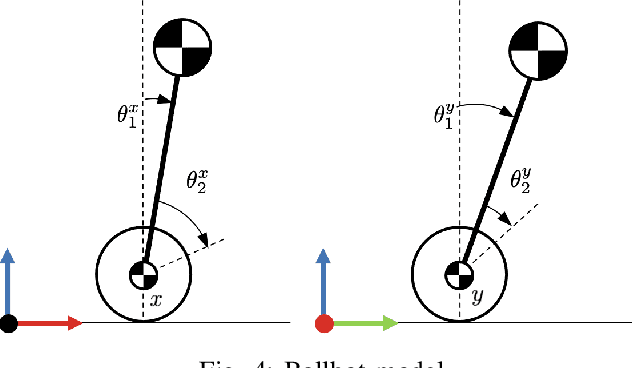
Topology-Informed Model Predictive Control for Anticipatory Collision Avoidance on a Ballbot

We focus on the problem of planning safe and efficient motion for a ballbot (i.e., a dynamically balancing mobile robot), navigating in a crowded environment. The ballbot's design gives rise to human-readable motion which is valuable for crowd navigation. However, dynamic stabilization introduces kinematic constraints that severely limit the ability of the robot to execute aggressive maneuvers, complicating collision avoidance and respect for human personal space. Past works reduce the need for aggressive maneuvering by motivating anticipatory collision avoidance through the use of human motion prediction models. However, multiagent behavior prediction is hard due to the combinatorial structure of the space. Our key insight is that we can accomplish anticipatory multiagent collision avoidance without high-fidelity prediction models if we capture fundamental features of multiagent dynamics. To this end, we build a model predictive control architecture that employs a constant-velocity model of human motion prediction but monitors and proactively adapts to the unfolding homotopy class of crowd-robot dynamics by taking actions that maximize the pairwise winding numbers between the robot and each human agent. This results in robot motion that accomplishes statistically significantly higher clearances from the crowd compared to state-of-the-art baselines while maintaining similar levels of efficiency, across a variety of challenging physical scenarios and crowd simulators.

Low-Rank Principal Eigenmatrix Analysis

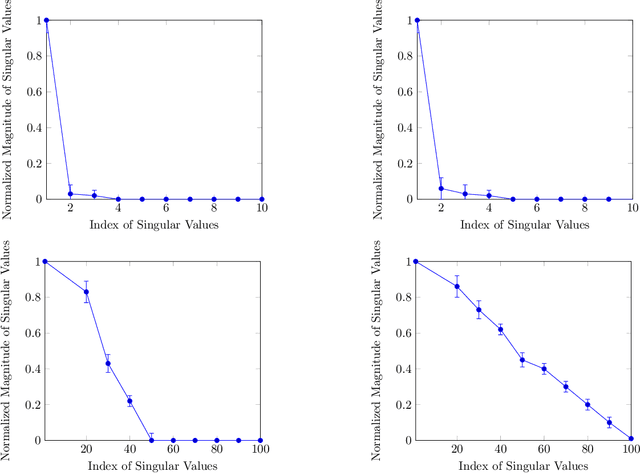
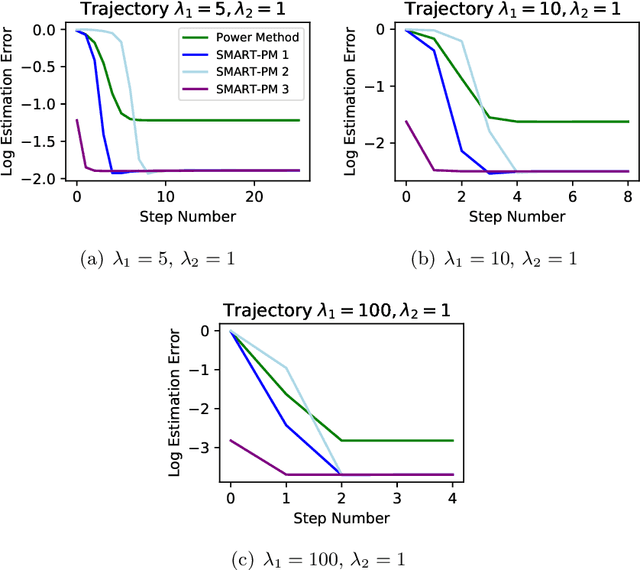
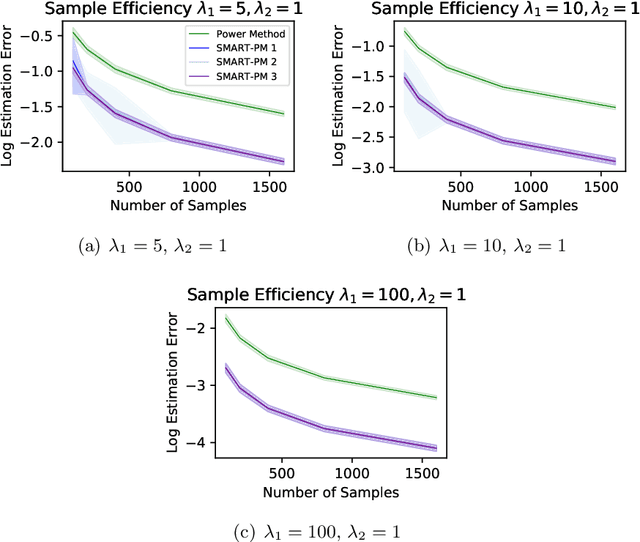
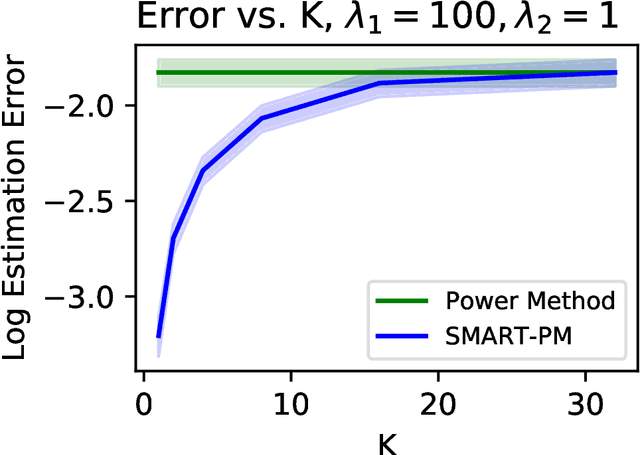
Sparse PCA is a widely used technique for high-dimensional data analysis. In this paper, we propose a new method called low-rank principal eigenmatrix analysis. Different from sparse PCA, the dominant eigenvectors are allowed to be dense but are assumed to have a low-rank structure when matricized appropriately. Such a structure arises naturally in several practical cases: Indeed the top eigenvector of a circulant matrix, when matricized appropriately is a rank-1 matrix. We propose a matricized rank-truncated power method that could be efficiently implemented and establish its computational and statistical properties. Extensive experiments on several synthetic data sets demonstrate the competitive empirical performance of our method.