Aiming towards the minimizers: fast convergence of SGD for overparametrized problems
Paper and Code
Jun 05, 2023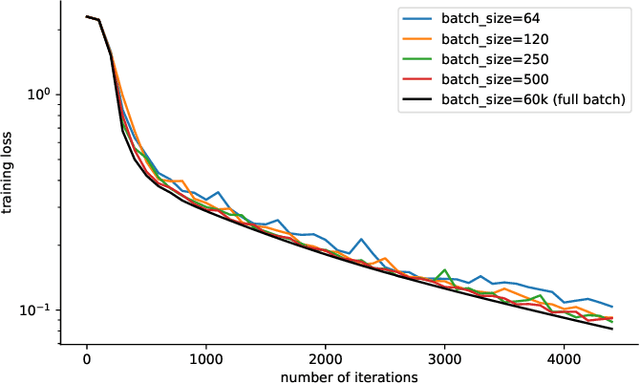
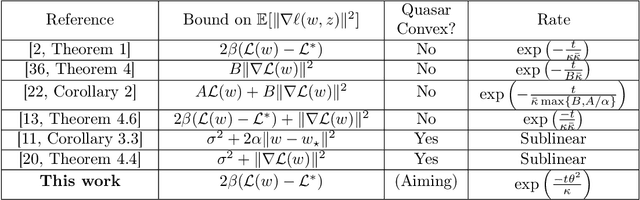
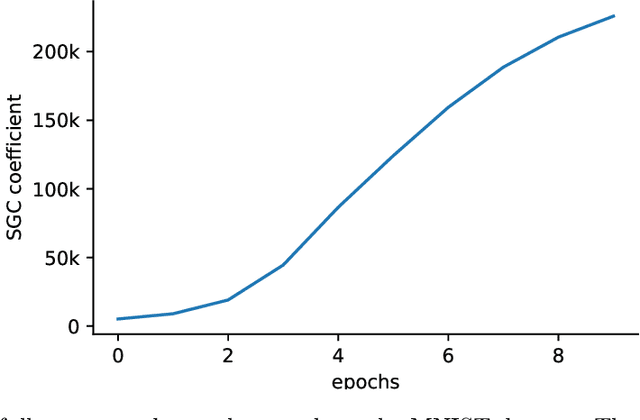
Modern machine learning paradigms, such as deep learning, occur in or close to the interpolation regime, wherein the number of model parameters is much larger than the number of data samples. In this work, we propose a regularity condition within the interpolation regime which endows the stochastic gradient method with the same worst-case iteration complexity as the deterministic gradient method, while using only a single sampled gradient (or a minibatch) in each iteration. In contrast, all existing guarantees require the stochastic gradient method to take small steps, thereby resulting in a much slower linear rate of convergence. Finally, we demonstrate that our condition holds when training sufficiently wide feedforward neural networks with a linear output layer.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge