Asymptotic normality and optimality in nonsmooth stochastic approximation
Paper and Code
Jan 16, 2023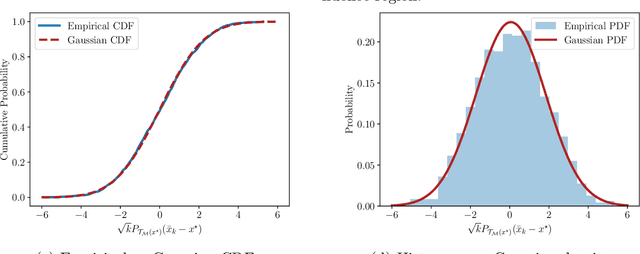
In their seminal work, Polyak and Juditsky showed that stochastic approximation algorithms for solving smooth equations enjoy a central limit theorem. Moreover, it has since been argued that the asymptotic covariance of the method is best possible among any estimation procedure in a local minimax sense of H\'{a}jek and Le Cam. A long-standing open question in this line of work is whether similar guarantees hold for important non-smooth problems, such as stochastic nonlinear programming or stochastic variational inequalities. In this work, we show that this is indeed the case.
* The arxiv report arXiv:2108.11832 has been split into two parts. This
is Part 2 of the original submission, augmented by a some new results and a
reworked exposition
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge