Clustering a Mixture of Gaussians with Unknown Covariance
Paper and Code
Oct 04, 2021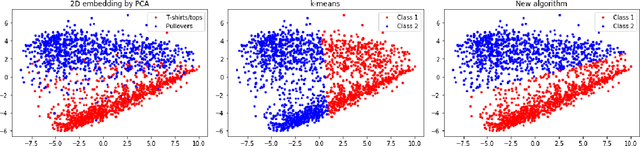

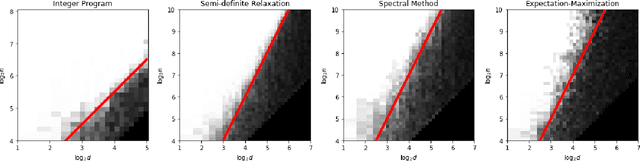
We investigate a clustering problem with data from a mixture of Gaussians that share a common but unknown, and potentially ill-conditioned, covariance matrix. We start by considering Gaussian mixtures with two equally-sized components and derive a Max-Cut integer program based on maximum likelihood estimation. We prove its solutions achieve the optimal misclassification rate when the number of samples grows linearly in the dimension, up to a logarithmic factor. However, solving the Max-cut problem appears to be computationally intractable. To overcome this, we develop an efficient spectral algorithm that attains the optimal rate but requires a quadratic sample size. Although this sample complexity is worse than that of the Max-cut problem, we conjecture that no polynomial-time method can perform better. Furthermore, we gather numerical and theoretical evidence that supports the existence of a statistical-computational gap. Finally, we generalize the Max-Cut program to a $k$-means program that handles multi-component mixtures with possibly unequal weights. It enjoys similar optimality guarantees for mixtures of distributions that satisfy a transportation-cost inequality, encompassing Gaussian and strongly log-concave distributions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge